本文主要是介绍代码随想录第29天|491.递增子序列 46.全排列 47.全排列 II,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录:
491.递增子序列
46.全排列
47.全排列 II
491.递增子序列
491. 非递减子序列 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
回溯算法精讲,树层去重与树枝去重 | LeetCode:491.递增子序列_哔哩哔哩_bilibili
给你一个整数数组
nums,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]示例 2:
输入:nums = [4,4,3,2,1] 输出:[[4,4]]提示:
1 <= nums.length <= 15-100 <= nums[i] <= 100
第一反应是把所有的子序列列出来,然后再判断是不是递增子序列。

回溯三部曲:
1、确定参数:除了path、result和startIndex之外,还需要一个集合来存放一层的值,避免在同一层中出现重复的值从而出现重复的子序列:
// 声明一个结果集合,用于存储所有满足条件的子序列List<List<Integer>> result = new ArrayList<>();// 声明一个路径集合,用于存储当前正在构建的子序列List<Integer> path = new ArrayList<>();HashSet<Integer> hs = new HashSet<>();private void backTracking(int[] nums, int startIndex) {
}2、确定终止条件:当path的大小大于1,且path里面的值符合曾序序列的要求时,把path加到result数组里,然后返回:
if (path.size() >= 2)result.add(new ArrayList<>(path));3、确定单层搜索的逻辑:
同一父节点下同层元素中,如果一个数字在同层已经出现过的话,就不能再使用了,因为再次使用的话会出现重复子序列:
for (int i = startIndex; i < nums.length; i++) {// 如果当前路径不为空,并且路径中的最后一个数字大于当前数字,或者当前数字已经在路径中出现过,则跳过当前数字if (!path.isEmpty() && path.get(path.size() - 1) > nums[i] || hs.contains(nums[i]))continue;// 将当前数字加入到路径中hs.add(nums[i]);path.add(nums[i]);// 递归调用,继续寻找以当前数字结尾的子序列backTracking(nums, i + 1);// 回溯,将当前数字从路径中移除,准备尝试其他可能的数字path.remove(path.size() - 1);}综合代码:
// 定义一个名为 Solution 的类
class Solution {// 声明一个结果集合,用于存储所有满足条件的子序列List<List<Integer>> result = new ArrayList<>();// 声明一个路径集合,用于存储当前正在构建的子序列List<Integer> path = new ArrayList<>();// 主方法,入口点public List<List<Integer>> findSubsequences(int[] nums) {// 调用回溯函数,开始查找所有满足条件的子序列backTracking(nums, 0);// 返回结果集合return result;}// 回溯函数,用于查找所有满足条件的子序列private void backTracking(int[] nums, int startIndex) {// 如果当前路径的长度大于等于2,则将其加入到结果集合中if (path.size() >= 2)result.add(new ArrayList<>(path)); // 创建一个哈希集合,用于记录当前路径中已经出现过的数字HashSet<Integer> hs = new HashSet<>();// 遍历数组,从startIndex位置开始for (int i = startIndex; i < nums.length; i++) {// 如果当前路径不为空,并且路径中的最后一个数字大于当前数字,或者当前数字已经在路径中出现过,则跳过当前数字if (!path.isEmpty() && path.get(path.size() - 1) > nums[i] || hs.contains(nums[i]))continue;// 将当前数字加入到路径中hs.add(nums[i]);path.add(nums[i]);// 递归调用,继续寻找以当前数字结尾的子序列backTracking(nums, i + 1);// 回溯,将当前数字从路径中移除,准备尝试其他可能的数字path.remove(path.size() - 1);}}
}
这里仍然有一个小疑惑:为什么hs里面的数不需要弹出呢?
46.全排列
. - 力扣(LeetCode)
代码随想录 (programmercarl.com)
组合与排列的区别,回溯算法求解的时候,有何不同?| LeetCode:46.全排列_哔哩哔哩_bilibili
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]示例 3:
输入:nums = [1] 输出:[[1]]提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
这道题我第一次看到的时候觉得就是每个位置上每个数字都可以放,但是不知道怎么代码实现。看了卡哥视频:
回溯三部曲:
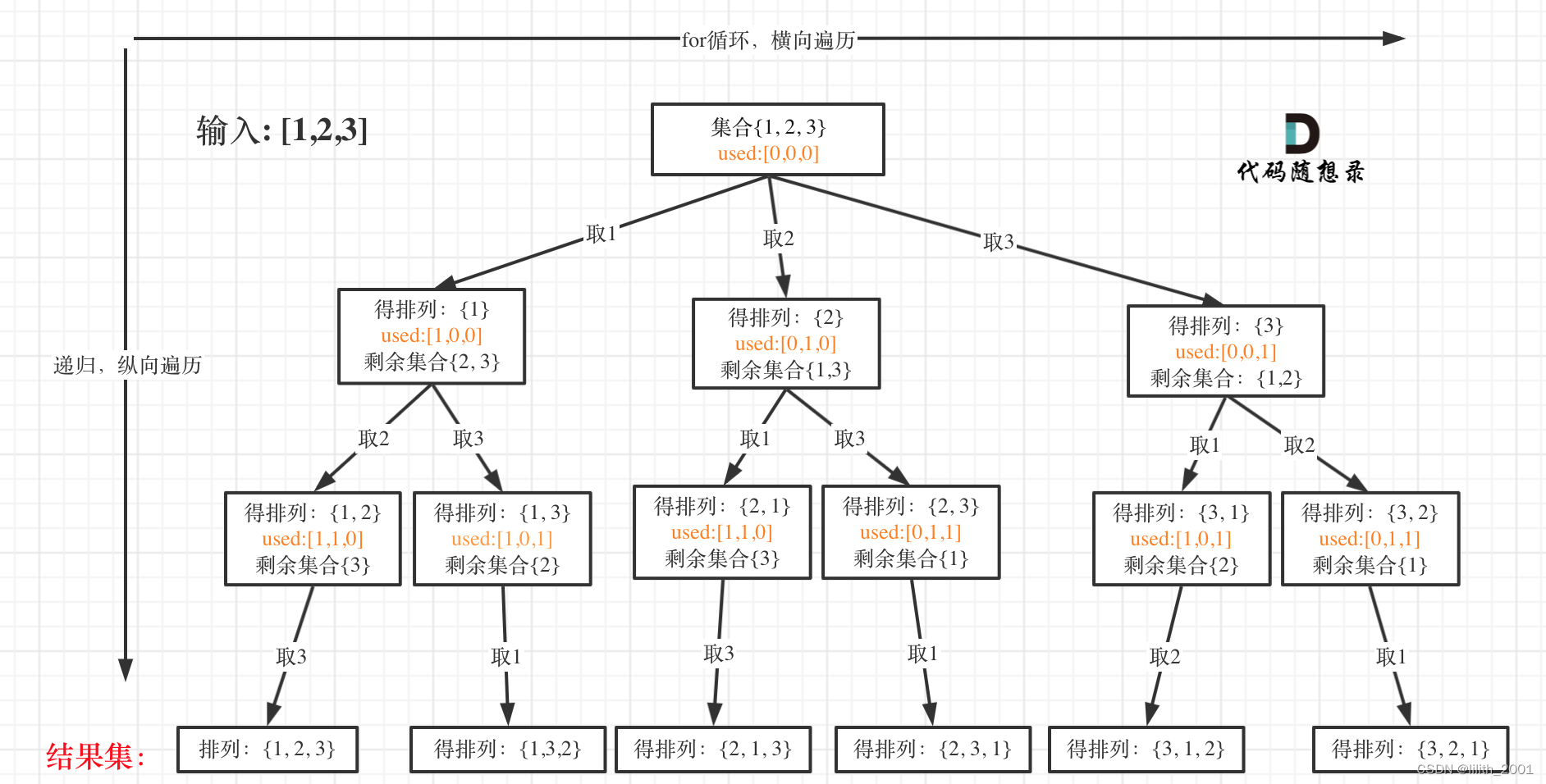
1、确定参数:排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
但排列问题需要一个used数组,标记已经选择的元素。
List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
boolean[] used; // 用于标记数字是否被使用过2、确定终止条件:叶子节点终止,即path长度和nums数组的大小一样时终止:
if (path.size() == nums.length){// 将当前路径加入到结果集合中result.add(new ArrayList<>(path));return;}3、确定单层搜索的逻辑:
// 遍历数组中的每个元素for (int i = 0; i < nums.length; i++){// 如果该元素已经被使用过,则跳过if (used[i]){continue;}// 标记该元素为已使用used[i] = true;// 将该元素加入到当前路径中path.add(nums[i]);// 递归调用,继续生成全排列结果permuteHelper(nums);// 回溯,将当前加入的元素移除path.removeLast();// 标记该元素为未使用used[i] = false;}综合代码:
class Solution {List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果boolean[] used; // 用于标记数字是否被使用过// 主函数,输入数组 nums,返回其全排列结果public List<List<Integer>> permute(int[] nums) {// 如果数组为空,则直接返回结果集合if (nums.length == 0){return result;}// 初始化 used 数组为与 nums 相同长度的布尔数组used = new boolean[nums.length];// 调用递归函数进行全排列permuteHelper(nums);// 返回全排列结果return result;}// 辅助递归函数,用于生成全排列结果private void permuteHelper(int[] nums){// 如果当前路径长度等于数组长度,表示已经得到一个全排列结果if (path.size() == nums.length){// 将当前路径加入到结果集合中result.add(new ArrayList<>(path));return;}// 遍历数组中的每个元素for (int i = 0; i < nums.length; i++){// 如果该元素已经被使用过,则跳过if (used[i]){continue;}// 标记该元素为已使用used[i] = true;// 将该元素加入到当前路径中path.add(nums[i]);// 递归调用,继续生成全排列结果permuteHelper(nums);// 回溯,将当前加入的元素移除path.removeLast();// 标记该元素为未使用used[i] = false;}}
}
47.全排列 II
47. 全排列 II - 力扣(LeetCode)
代码随想录 (programmercarl.com)
回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II_哔哩哔哩_bilibili
给定一个可包含重复数字的序列
nums,按任意顺序 返回所有不重复的全排列示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]提示:
1 <= nums.length <= 8-10 <= nums[i] <= 10
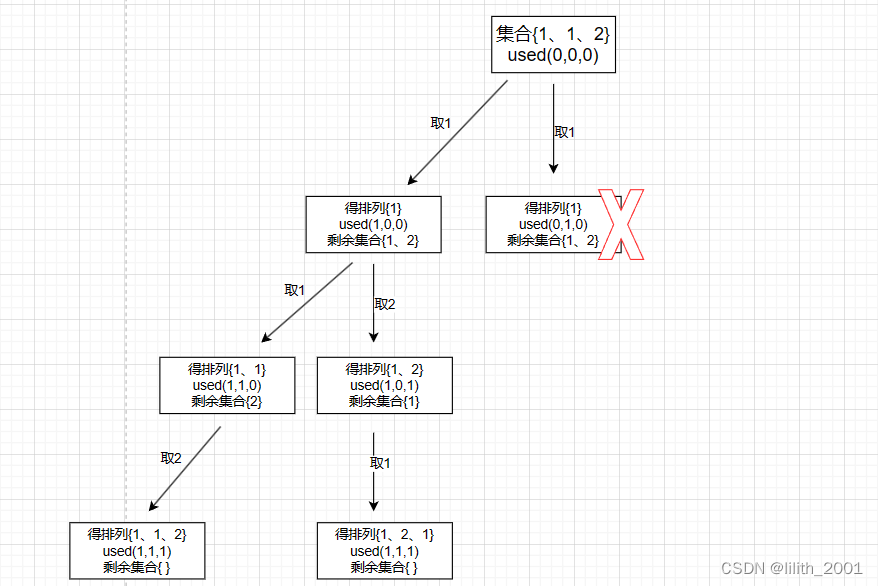
如图,还是要考虑一个去重的逻辑。
1、确定参数:
// 存放结果List<List<Integer>> result = new ArrayList<>();// 暂存结果List<Integer> path = new ArrayList<>();
// 标记每个数字是否被使用过boolean[] used = new boolean[nums.length];2、确定终止条件:
// 如果当前路径长度等于数组长度,说明已经找到一个排列if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 将当前路径加入结果集return; // 结束当前递归}3、确定单层搜索逻辑:used[i-1]为false的时候,才保证了是树层上的数值不能相同,而不是树枝上。
// 遍历所有数字for (int i = 0; i < nums.length; i++) {// 如果当前数字已经被使用过,直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}// 如果当前数字未被使用过,开始处理if (used[i] == false) {used[i] = true; // 标记当前数字被使用过path.add(nums[i]); // 将当前数字加入路径backTrack(nums, used); // 递归处理下一层path.remove(path.size() - 1); // 回溯,移除当前数字used[i] = false; // 恢复当前数字的未使用状态}}
综合代码:
class Solution {// 存放结果List<List<Integer>> result = new ArrayList<>();// 暂存结果List<Integer> path = new ArrayList<>();// 主函数,入口public List<List<Integer>> permuteUnique(int[] nums) {// 标记每个数字是否被使用过boolean[] used = new boolean[nums.length];Arrays.fill(used, false); // 初始化为未使用状态Arrays.sort(nums); // 对输入数组排序,确保相同数字相邻backTrack(nums, used); // 调用回溯函数return result; // 返回最终结果}// 回溯函数,用于搜索所有排列组合private void backTrack(int[] nums, boolean[] used) {// 如果当前路径长度等于数组长度,说明已经找到一个排列if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 将当前路径加入结果集return; // 结束当前递归}// 遍历所有数字for (int i = 0; i < nums.length; i++) {// 如果当前数字已经被使用过,直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}// 如果当前数字未被使用过,开始处理if (used[i] == false) {used[i] = true; // 标记当前数字被使用过path.add(nums[i]); // 将当前数字加入路径backTrack(nums, used); // 递归处理下一层path.remove(path.size() - 1); // 回溯,移除当前数字used[i] = false; // 恢复当前数字的未使用状态}}}
}
这篇关于代码随想录第29天|491.递增子序列 46.全排列 47.全排列 II的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







