本文主要是介绍【经典算法】LeetCode101:对称二叉树(Java/C/Python3实现含注释说明,Easy),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对称二叉树
- 题目描述
- 思路及实现
- 方式一:递归(推荐)
- 思路
- 代码实现
- Java版本
- C语言版本
- Python3版本
- 复杂度分析
- 方式二:队列(迭代)
- 思路
- 代码实现
- Java版本
- C语言版本
- Python3版本
- 复杂度分析
- 总结
- 相似题目
- 标签:二叉树递归、对称性判断
题目描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
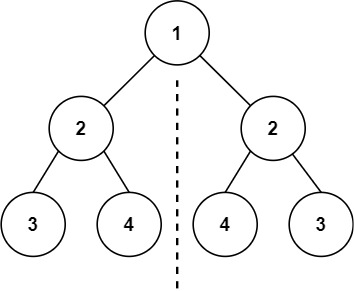
输入:root = [1,2,2,3,4,4,3] 输出:true 示例 2:
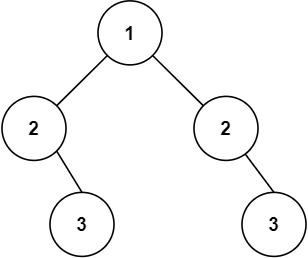
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100进阶:你可以运用递归和迭代两种方法解决这个问题吗?
原题: LeetCode 101
思路及实现
方式一:递归(推荐)
思路
乍一看无从下手,但用递归其实很好解决。
根据题目的描述,镜像对称,就是左右两边相等,也就是左子树和右子树是相当的。
注意这句话,左子树和右子相等,也就是说要递归的比较左子树和右子树。
我们将根节点的左子树记做 left,右子树记做 right。比较 left 是否等于 right,不等的话直接返回就可以了。
如果相当,比较 left 的左节点和 right 的右节点,再比较 left 的右节点和 right 的左节点
比如看下面这两个子树(他们分别是根节点的左子树和右子树),能观察到这么一个规律:
左子树 2 的左孩子 == 右子树 2 的右孩子
左子树 2 的右孩子 == 右子树 2 的左孩子
根据上面信息可以总结出递归函数的两个终止条件:
- left 和 right 不等,或者 left 和 right 都为空
- 递归的比较 left,left 和 right.right,递归比较
left,right 和 right.left
代码实现
Java版本
class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) {return true; // 如果根节点为null,即空树,视为对称二叉树,返回true}return isMirror(root.left, root.right); // 调用isMirror方法判断左子树和右子树是否对称}private boolean isMirror(TreeNode left, TreeNode right) {if (left == null && right == null) {return true; // 如果左子树和右子树都为null,也视为对称,返回true}if (left == null || right == null) {return false; // 如果左子树和右子树只有一个为null,视为不对称,返回false}return left.val == right.val && isMirror(left.left, right.right) && isMirror(left.right, right.left);// 如果左子树和右子树的值相等,且同时满足左子树的左子树和右子树的右子树对称,// 以及左子树的右子树和右子树的左子树对称,则视为对称,返回true;否则,返回false}
}说明:
isSymmetric方法是该函数的入口,接收一个二叉树的根节点作为参数。首先判断根节点是否为null,如果是,即空树,视为对称二叉树,返回true。否则,调用isMirror 方法来判断左子树和右子树是否对称。isMirror方法是递归判断左右子树是否对称的函数。首先判断左子树和右子树是否都为null,如果是,即均为空树,视为对称,返回true。然后判断左子树和右子树中只有一个为null的情况,即一个为空树一个不为空树,视为不对称,返回false。最后,判断左子树的值和右子树的值是否相等,并且同时递归判断左子树的左子树和右子树的右子树是否对称,以及递归判断左子树的右子树和右子树的左子树是否对称。只有全部满足才视为对称,返回true;否则,返回false。
C语言版本
#include <stdbool.h>/*struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};
*/bool isMirror(struct TreeNode *left, struct TreeNode *right);bool isSymmetric(struct TreeNode *root) {if (root == NULL) {return true; // 如果根节点为NULL,即空树,视为对称二叉树,返回true}return isMirror(root->left, root->right); // 调用isMirror函数判断左子树和右子树是否对称
}bool isMirror(struct TreeNode *left, struct TreeNode *right) {if (left == NULL && right == NULL) {return true; // 如果左子树和右子树都为NULL,也视为对称,返回true}if (left == NULL || right == NULL) {return false; // 如果左子树和右子树只有一个为NULL,视为不对称,返回false}return (left->val == right->val) && isMirror(left->left, right->right) && isMirror(left->right, right->left);// 如果左子树和右子树的值相等,并且同时满足左子树的左子树和右子树的右子树对称,// 以及左子树的右子树和右子树的左子树对称,则视为对称,返回true;否则,返回false
}Python3版本
class Solution:def isSymmetric(self, root: TreeNode) -> bool:if root is None:return True # 如果根节点为空,返回True,空树被认为是对称的return self.isMirror(root.left, root.right)def isMirror(self, left: TreeNode, right: TreeNode) -> bool:if left is None and right is None:return True # 如果左子树和右子树都为空,认为是对称的if left is None or right is None:return False # 如果左子树和右子树只有一个为空,不对称return left.val == right.val and self.isMirror(left.left, right.right) and self.isMirror(left.right, right.left)# 比较左子树的左子树和右子树的右子树,以及左子树的右子树和右子树的左子树,满足条件才认为是对称的# 假设定义了TreeNode类,包含val、left和right属性
class TreeNode:def __init__(self, val: int = 0, left: TreeNode = None, right: TreeNode = None):self.val = valself.left = leftself.right = right说明:代码中使用了 TreeNode 类来定义树节点,包含 val、left 和 right 属性。其中 val 存储节点的值,left 和
right 存储左子树和右子树的引用。
复杂度分析
- 时间复杂度:O(n),其中 n 表示树的节点数。
- 空间复杂度:O(n),递归调用的栈空间最多为树的高度。
方式二:队列(迭代)
思路
回想下递归的实现:
当两个子树的根节点相等时,就比较:
左子树的 left 和 右子树的 right,这个比较是用递归实现的。
现在我们改用队列来实现,思路如下:
首先从队列中拿出两个节点(left 和 right)比较:
将 left 的 left 节点和 right 的 right 节点放入队列
将 left 的 right 节点和 right 的 left 节点放入队列
代码实现
Java版本
//leetcode submit region begin(Prohibit modification and deletion)
import java.util.LinkedList;class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) {return false; // 根节点为空,不算对称}if (root.left == null && root.right == null) {return true; // 左右子树都为空,算对称}LinkedList<TreeNode> queue = new LinkedList(); // 使用队列来保存待比较的节点queue.add(root.left);queue.add(root.right);while (queue.size() > 0) {TreeNode left = queue.removeFirst();TreeNode right = queue.removeFirst();// 只要两个节点都为空,继续循环;两者有一个为空,返回falseif (left == null && right == null) {continue;}if (left == null || right == null) {return false;}// 判断两个节点的值是否相等if (left.val != right.val) {return false;}// 将左节点的左子节点和右节点的右子节点放入队列queue.add(left.left);queue.add(right.right);// 将左节点的右子节点和右节点的左子节点放入队列queue.add(left.right);queue.add(right.left);}return true;}
}
//leetcode submit region end(Prohibit modification and deletion)说明:
这段代码使用迭代方法判断二叉树是否对称。在 isSymmetric 方法中,首先判断根节点是否为空,如果为空,返回 false,表示不对称。然后,如果根节点的左右子树都为空,返回 true,表示对称(只有一个元素的case)。
接下来,创建一个队列 queue,并将根节点的左子节点和右子节点加入队列。然后进入循环,每次从队列中取出两个节点进行比较。在比较过程中,只要两个节点均为空,继续循环;如果只有一个节点为空,返回
false,表示不对称。然后,比较两个节点的值是否相等,如果不相等,返回 false。将左节点的左子节点和右节点的右子节点放入队列,用于后续比较。同时,将左节点的右子节点和右节点的左子节点放入队列,也用于后续比较。
当队列为空时,表示所有节点都已比较完毕,没有发现不对称的情况,返回 true,表示对称。
这段代码使用了迭代方法,利用队列存储待比较的节点,逐层按顺序比较,避免了递归方法的额外栈空间开销。
C语言版本
// leetcode submit region begin(Prohibit modification and deletion)
#include <stdbool.h>struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};bool isSymmetric(struct TreeNode* root) {if (root == NULL) {return false; // 根节点为空,不算对称}struct TreeNode* queue[10000]; // 使用队列来保存待比较的节点int front = 0, rear = 0;queue[rear++] = root->left;queue[rear++] = root->right;while (rear != front) {struct TreeNode* left = queue[front++];struct TreeNode* right = queue[front++];// 只要两个节点都为空,继续循环;两者有一个为空,返回falseif (left == NULL && right == NULL) {continue;}if (left == NULL || right == NULL) {return false;}// 判断两个节点的值是否相等if (left->val != right->val) {return false;}// 将左节点的左子节点和右节点的右子节点放入队列queue[rear++] = left->left;queue[rear++] = right->right;// 将左节点的右子节点和右节点的左子节点放入队列queue[rear++] = left->right;queue[rear++] = right->left;}return true;
}
//leetcode submit region end(Prohibit modification and deletion)说明:
这段代码使用C语言实现了迭代方法来判断二叉树是否对称。在 isSymmetric 函数中,首先判断根节点是否为空,如果为空,返回 false,表示不对称。
创建一个队列 queue,使用数组来保存待比较的节点。使用 front 和 rear 变量分别表示队首和队尾的索引。
将根节点的左子节点和右子节点依次加入队列 queue。
然后进入循环,每次从队列中取出两个节点进行比较。
在比较过程中,只要两个节点均为空,继续循环;如果只有一个节点为空,返回
false,表示不对称。然后,比较两个节点的值是否相等,如果不相等,返回 false。将左节点的左子节点和右节点的右子节点放入队列,用于后续比较。同时,将左节点的右子节点和右节点的左子节点放入队列,也用于后续比较。
当队列为空时,表示所有节点都已比较完毕,没有发现不对称的情况,返回 true,表示对称。
这段代码使用了迭代方法,利用数组队列方式存储待比较的节点,逐个按序比较,避免了递归方法的额外栈空间开销。
Python3版本
class Solution:def isSymmetric(self, root: TreeNode) -> bool:if root is None:return False # 根节点为空,不算对称queue = []queue.append(root.left)queue.append(root.right)while queue:left = queue.pop(0)right = queue.pop(0)if left is None and right is None:continue # 只要两个节点都为空,继续循环if left is None or right is None:return False # 两者有一个为空,返回False,不对称if left.val != right.val:return False # 节点值不相等,不对称queue.append(left.left) # 左节点的左子节点入队列queue.append(right.right) # 右节点的右子节点入队列queue.append(left.right) # 左节点的右子节点入队列queue.append(right.left) # 右节点的左子节点入队列return True # 队列为空,所有节点比较完毕,对称说明:(基础说明可查看java或者c的实现)
在函数参数的类型注解中,使用了 TreeNode 类型来标注 root 参数的类型。
使用了 is 运算符来判断节点是否为 None。is 运算符比较的是对象的身份标识,用于判断对象是否是同一个对象。这里用它来判断节点是否为None。
使用了列表 queue 来实现队列的功能,通过 append() 方法将节点加入队列的尾部,通过 pop(0)
方法来从队列的头部取出节点。Python的列表可以很方便地实现队列的功能。
复杂度分析
- 时间复杂度:O(n),其中 n 表示树的节点数。在最坏情况下,需要遍历树的所有节点。
- 空间复杂度:O(n),最坏情况下,队列中需要存储树的一层节点,所以空间复杂度与树的高度有关。在最坏情况下,树的高度为 n/2,因此空间复杂度为 O(n)。
综合来看,这个算法的时间复杂度和空间复杂度都是 O(n),其中 n 表示树的节点数。算法的性能随着节点数的增加而线性增长。
总结
| 方法 | 优点 | 缺点 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|---|
| 递归法 | - 直观易懂 - 代码相对简洁 | - 可能导致函数调用栈溢出的风险 - 需要额外的空间来存储函数调用栈 | O(n) | O(n) |
| 队列法 | - 不会导致函数调用栈溢出的风险 - 无需递归,代码较为直观 - 灵活的节点入队和出队顺序 | - 需要手动维护队列数据结构和追踪节点的层次 - 需要额外的空间来存储队列和节点的信息 | O(n) | O(m) |
相似题目
| 题目 | 描述 | 难度 |
|---|---|---|
| LeetCode 100 | 判断两个二叉树是否相同 | Easy |
| LeetCode 226 | 反转二叉树 | Easy |
| LeetCode 104 | 计算二叉树的最大深度 | Easy |
| LeetCode 110 | 判断二叉树是否平衡 | Easy |
| LeetCode 222 | 统计完全二叉树的节点个数 | Medium |
| LeetCode 124 | 计算二叉树中的最大路径和 | Hard |
| LeetCode 199 | 返回二叉树从右侧看的节点值列表 | Medium |
| LeetCode 116 | 填充二叉树的每个节点的下一个右侧节点指针 | Medium |
| LeetCode 112 | 判断二叉树是否存在从根节点到叶子节点的路径和等于给定目标值 | Easy |
| LeetCode 257 | 返回二叉树所有从根节点到叶子节点的路径 | Easy |
这篇关于【经典算法】LeetCode101:对称二叉树(Java/C/Python3实现含注释说明,Easy)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!