本文主要是介绍浅析扩散模型与图像生成【应用篇】(十五)——SDG,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
15. More Control for Free! Image Synthesis with Semantic Diffusion Guidance
该文提出一种基于语义引导扩散模型的的图像生成算法,SDG,可使用文本或图像作为引导来指引图像的生成,也可以二者同时使用,实现多模态的引导。增加引导信息无需对扩散模型进行微调训练,可以直接作用在生成阶段。相对于现有的文本引导图像生成方法StyleCLIP或图像引导生成方法ILVR,SDG不仅能够适应更多模态的输入,且生成样本也具备更大的多样性。
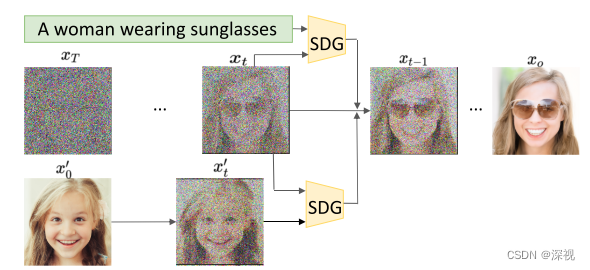
在ADM这篇论文中,作者提出一种基于分类器引导的扩散模型,通过额外训练一个分类器 p ϕ ( y ∣ x t , t ) p_{\phi}(y|x_t,t) pϕ(y∣xt,t),并计算分类器对输入 x t x_t xt的对数梯度 ∇ x t log p ϕ ( y ∣ x t ) \nabla_{x_{t}} \log p_{\phi}\left(y \mid x_{t}\right) ∇xtlogpϕ(y∣xt),将其乘以一个系数加到原本去噪模型估计得到的均值 μ \mu μ上,就可以实现对扩散模型的引导。相当于根据分类器的偏好改变了噪声估计的分布,使其均值向分类器的梯度方向移动。具体实现方式如下 μ , Σ ← μ θ ( x t ) , Σ θ ( x t ) x t − 1 ← sample from N ( μ + s Σ ∇ x t log p ϕ ( y ∣ x t ) , Σ ) \begin{array}{l} \mu, \Sigma \leftarrow \mu_{\theta}\left(x_{t}\right), \Sigma_{\theta}\left(x_{t}\right) \\ x_{t-1} \leftarrow \text { sample from } \mathcal{N}\left(\mu+s \Sigma \nabla_{x_{t}} \log p_{\phi}\left(y \mid x_{t}\right), \Sigma\right)\end{array} μ,Σ←μθ(xt),Σθ(xt)xt−1← sample from N(μ+sΣ∇xtlogpϕ(y∣xt),Σ) 本文的方法借鉴了ADM的思想,只是将分类器引导拓展到更一般的语义引导,使用一个引导函数 F ϕ ( x t , y , t ) F_{\phi}(x_t,y,t) Fϕ(xt,y,t)取代了计算分类器对数 log p ϕ ( y ∣ x t ) \log p_{\phi}\left(y \mid x_{t}\right) logpϕ(y∣xt)的过程,针对不同的引导方式,引导函数有不同的定义。SDG的计算过程如下

1. 文本引导
作者采用了CLIP中的文本编码器 E L E_L EL和图像编码器 E I E_I EI来分别计算引导文本 l l l和生成图像 x t x_t xt对应的嵌入特征。有一点需要注意的是,由于CLIP中的图像编码器 E I E_I EI只能根据输入图像 x t x_t xt进行编码,而没有考虑时刻 t t t这一条件,因此作者对 E I E_I EI进行了小小的改动,利用AdaGN层将时刻 t t t引入编码过程,得到了时间依赖的图像编码器 E I ′ ( x t , t ) E_I'(x_t,t) EI′(xt,t)。最终文本引导函数定义如下 F ( x t , l , t ) = E I ′ ( x t , t ) ⋅ E L ( l ) F\left(x_{t}, l, t\right)=E_{I}^{\prime}\left(x_{t}, t\right) \cdot E_{L}(l) F(xt,l,t)=EI′(xt,t)⋅EL(l)
2. 图像引导
针对图像引导的情况,作者给出了多种引导方式,包括:图像内容引导,图像结构引导和图像风格引导。内容引导是指生成与引导图像包含相似内容的图像,如根据一张猫的照片,生成另一张猫的照片。内容引导本身不对生成结果的姿态或者空间布局情况进行限制,因此生成结果会包含更多不同的姿态和空间布局情况。而结构引导则更多的侧重于空间维度上的对齐。风格引导,则是注重图像全局风格上的一致性,如生成具有梵高绘画风格的照片。具体的计算过程分别如下:
图像内容引导 F ( x t , x t ′ , t ) = E I ′ ( x t , t ) ⋅ E I ′ ( x t ′ , t ) F\left(x_{t}, x_{t}^{\prime}, t\right)=E_{I}^{\prime}\left(x_{t}, t\right) \cdot E_{I}^{\prime}\left(x_{t}^{\prime}, t\right) F(xt,xt′,t)=EI′(xt,t)⋅EI′(xt′,t)
图像结构引导 F ( x t , x t ′ , t ) = − ∑ j 1 C j H j W j ∥ E I ′ ( x t , t ) j − E I ′ ( x t ′ , t ) j ∥ 2 2 F\left(x_{t}, x_{t}^{\prime}, t\right)=-\sum_{j} \frac{1}{C_{j} H_{j} W_{j}}\left\|E_{I}^{\prime}\left(x_{t}, t\right)_{j}-E_{I}^{\prime}\left(x_{t}^{\prime}, t\right)_{j}\right\|_{2}^{2} F(xt,xt′,t)=−j∑CjHjWj1 EI′(xt,t)j−EI′(xt′,t)j 22
图像风格引导 F ( x t , x t ′ , t ) = − ∑ j ∥ G I ′ ( x t , t ) j − G I ′ ( x t ′ , t ) j ∥ F 2 F\left(x_{t}, x_{t}^{\prime}, t\right)=-\sum_{j}\left\|G_{I}^{\prime}\left(x_{t}, t\right)_{j}-G_{I}^{\prime}\left(x_{t}^{\prime}, t\right)_{j}\right\|_{F}^{2} F(xt,xt′,t)=−j∑ GI′(xt,t)j−GI′(xt′,t)j F2其中 x t ′ x'_t xt′是由输入的引导图像 x 0 ′ x_0' x0′经过 t t t步扩散过程得到的, G I ′ ( ) j G_I'()_j GI′()j表示计算 E I ′ E_I' EI′编码器输出的第 j j j层特征图的格拉姆矩阵。
格拉姆矩阵是表达图像风格常用的计算方式,本质是计算矩阵和自身转置矩阵之间的乘积,具体的介绍参见https://zhuanlan.zhihu.com/p/545090017
3. 多模态引导
正如前文所说,文本引导和图像引导可以同时使用来引导生成过程,实现方式是简单的将不同的引导函数进行加权求和,如下式 F ϕ 0 ( x t , y , t ) = s 1 F ϕ 1 ( x t , y , t ) + s 2 F ϕ 2 ( x t , y , t ) F_{\phi_{0}}\left(x_{t}, y, t\right)=s_{1} F_{\phi_{1}}\left(x_{t}, y, t\right)+s_{2} F_{\phi_{2}}\left(x_{t}, y, t\right) Fϕ0(xt,y,t)=s1Fϕ1(xt,y,t)+s2Fϕ2(xt,y,t)权重系数 s s s可以对生成结果进行控制,对于文本引导权重系数通常取 s = 120 s=120 s=120,而图像引导权重系数通常取 s = 100 s=100 s=100。权重系数越大,生成结果则与引导信息更加一致,但生成结果的多样性也会随之下降。不同引导模式的生成结果如下

这篇关于浅析扩散模型与图像生成【应用篇】(十五)——SDG的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



