本文主要是介绍Fluent后处理:获取任意方向的速度分量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题:
如何获取速度在任意方向的速度分量?
解决思路:
此问题的本质为计算向量在某个方向的投影。
1 在特定方向的投影
根据向量投影的定义,速度向量 v 在任意向量 n 上的投影 vn 计算公式为:

linear format 1: v_n=(v ⃗∙n ⃗)/|n ⃗ | =v ⃗∙(n_e ) ⃗
linear format 2: (v_n ) ⃗=v_n∙(n_e ) ⃗
上式运算:
- 向量 vn 和 向量 n 平行
- 数值结果其绝对值表示向量 vn 的模
- 数值结果为负号表示 vn 和 n 反向。
在 Fluent 中,计算 vn 可利用表达式,根据投影的定义计算投影,其表达式如图所示:

文字版:(Velocity.x*ne_x+Velocity.y*ne_y+Velocity.z*ne_z)/(1 [m])
上式中,ne_x、ne_y、ne_z分别为基于表达式定义的向量 ne 的坐标,包含长度单位,表达式计算结果的单位为速度单位 m/s。
对应的可计算 vn 的向量各坐标
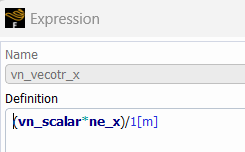
文字版:(vn_scalar*ne_x)/1[m]
2 在平面的投影
对于以向量 n 为法向的平面 p,速度向量 v 在平面 p 的投影 vp 和 vn 垂直。
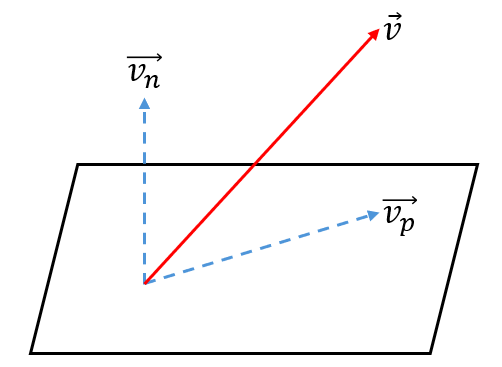
计算 vp 的操作称为 rejection,目前无公认的中文称呼。
vp和vn之间满足:

linear format: (v_p ) ⃗=v ⃗-(v_n ) ⃗
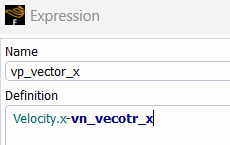
在Fluent中,可类似获得 vp 的向量各坐标
备注:向量点乘结果为数值,其计算公式:
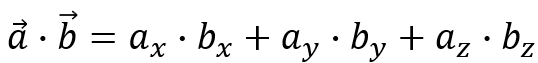
linear format: a ⃗∙b ⃗=a_x∙b_x+a_y∙b_y+a_z∙b_z
这篇关于Fluent后处理:获取任意方向的速度分量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



