165.乐理基础-关系大小调、同主音调、小调的调号判断

本文主要是介绍165.乐理基础-关系大小调、同主音调、小调的调号判断，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

如果到这五线谱还没记住还不认识的话去看102.五线谱-高音谱号与103.五线谱-低音谱号这两个里，这里面有五线谱对应的音名，对比着看

如果不认识调号去看112.五线谱的调号（一）113.五线谱的调号（二）114.快速识别五线谱的谱号

如果一章没落下，看到这里，但是看不懂什么意思，那就强行下看，看着看着指不定在某一个点就能全懂了

内容参考于：三分钟音乐社

上一个内容：164.和声小调、旋律小调

关系大小调：

关系大小调这个词有另外两个称呼，一个是平行大小调，一个是同音列大小调，这三个名字用的都很多，都是一样的意思

但是平行大小调这个词有一点歧义，这个歧义放在最后写，现在先用关系大小调这个词

关系大小调的意义，使用相同调号的大调与小调，或者说使用相同音名的大调与小调

比如C大调使用的音是CDEFGAB，A小调使用的是ABCDEFG，它们使用的音名都是一样的，只是主音不同，C为主音就是C大调、A为主音就是a小调，这就是使用相同音名的大调与小调，然后它们的调号也都是一样的，C大调与a小调都不会用到升降音，所以调号都是0升0降

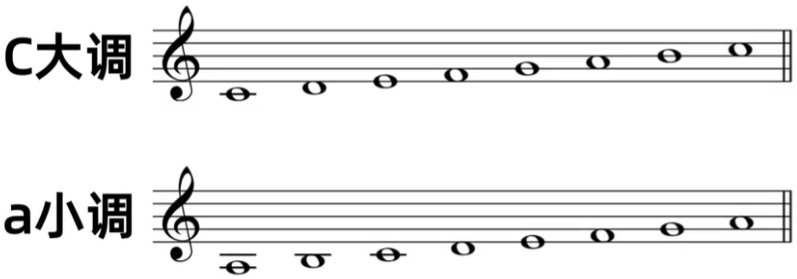
然后就可以说C大调是a小调的关系大调，a小调是C大调的关系小调，C大调与a小调互为关系大小调

然后再一个例子，D大调与b小调，D大调用的是DE升FGAB升C，b小调用的是B升CDE升FGA，它俩用的音名一样，也只是主音不一样，D为主音的就是D大调，b为主音的就是b小调，它们的调号也都是一样的，都涉及到升F与升C，其它5个音就没有涉及升降号，所以D大调与b小调就是一样的调号，也就是2个升号

然后怎么判断某个大调是和哪个小调形成关系大小调呢？这个是有规律的，下图是C大调与a小调

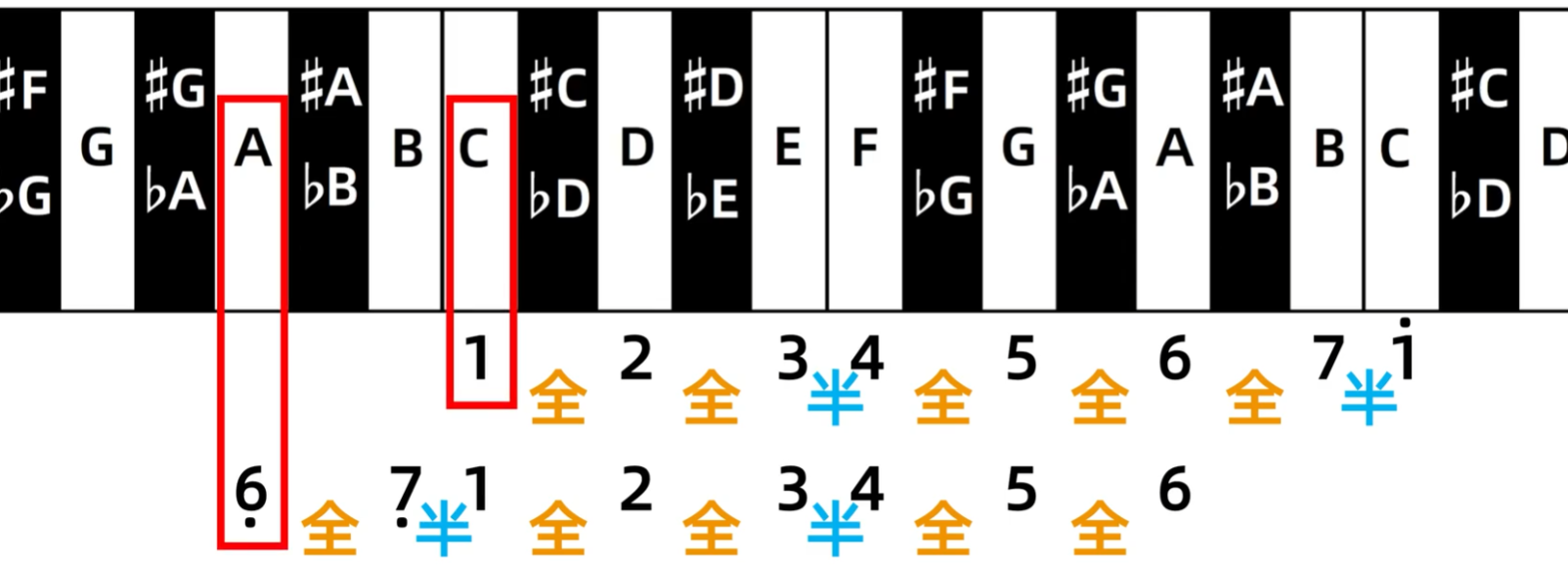
然后直接平移音名，就变成了b小调与D大调

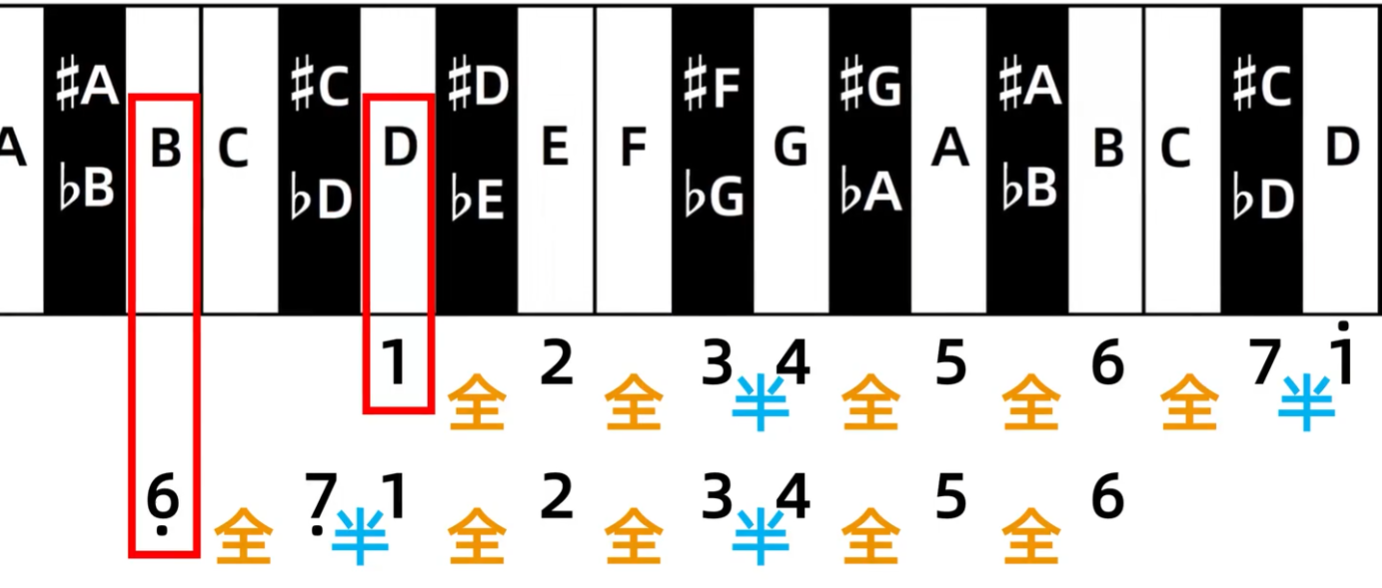
再平移e小调与G大调，G大调与e小调使用的音名一样，所以就互为关系大小调

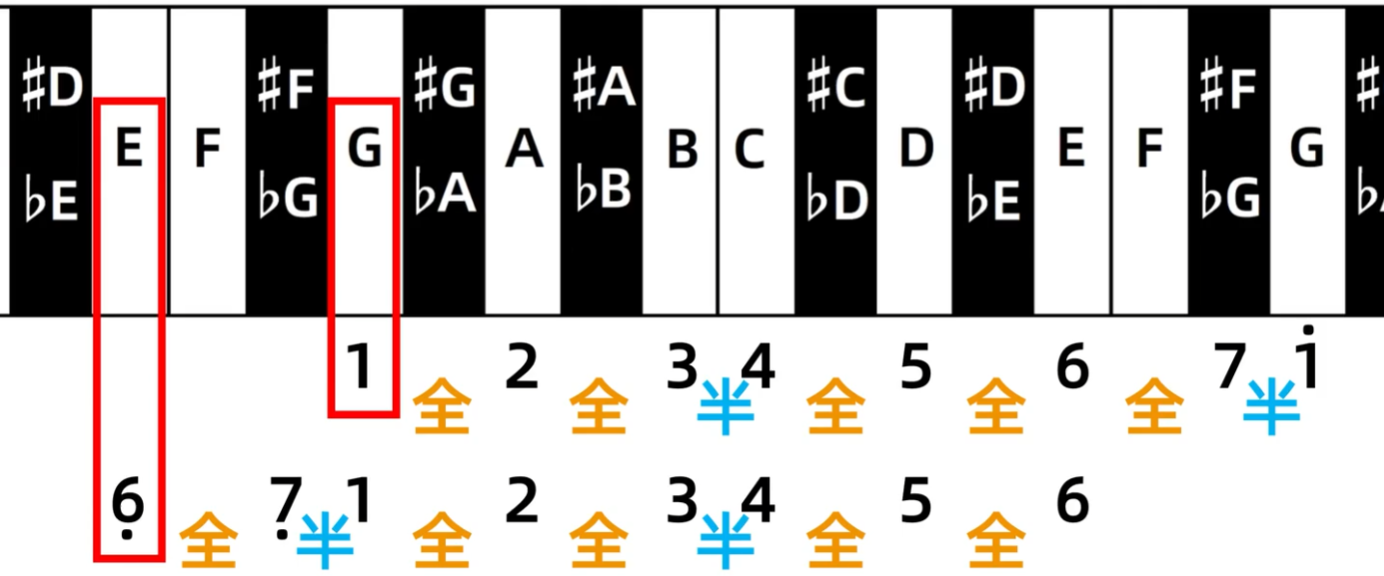
它们的主音都相差小三度，并且是大调的主音比关系小调的主音高小三度，从这一点中可以知道小调的调号是怎样来的了

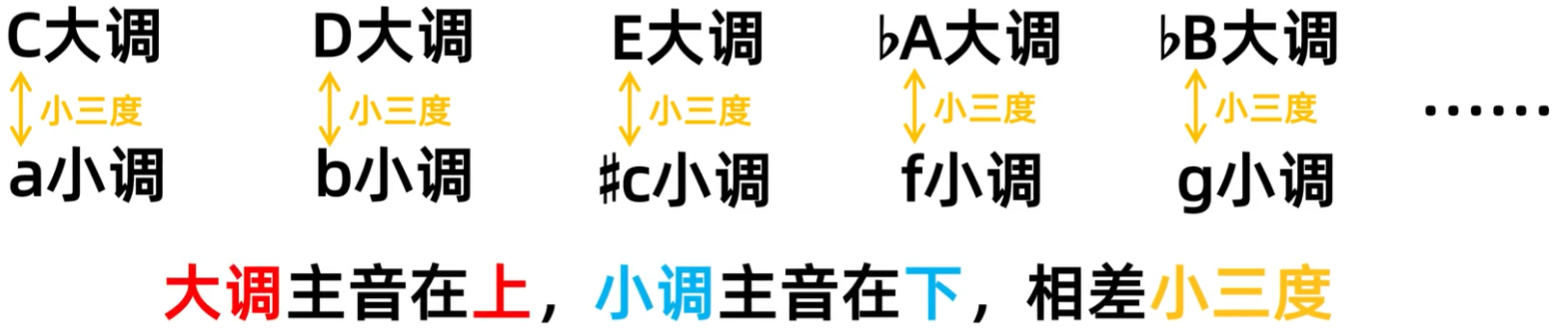
现在要保证搞懂了112.五线谱的调号（一）、113.五线谱的调号（二）、114.快速识别五线谱的谱号，它们三个里面是写的判断大调的方式

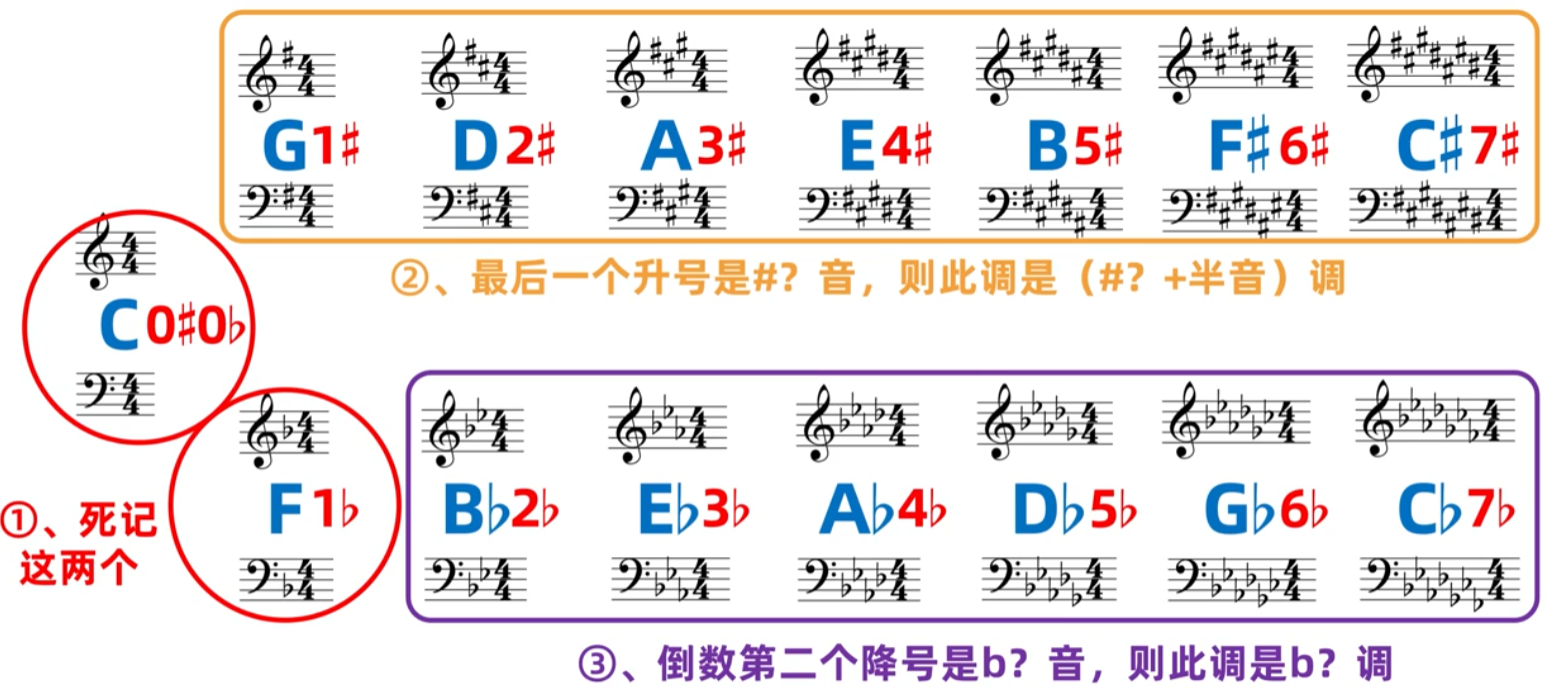
然后比如一个降号下图是F大调的调号，根据上方的内容就要知道，一个降号可能是F大调，也可能是F下方小三度的d，也就是d小调的调号

再比如三个升号，也就是A大调，根据上方的内容，也要知道它也可能是A下方小三度的升f小调的调号

然后只要记得大调主音往下小三度就是它的关系小调，然后在通过大调在五线谱上的形式，就可以知道小调是在五线谱上的形式是什么了

然后一个调号有可能是大调，有可能是小调，那该怎样判断是大调还是小调，调式的准确判断要结合和声，没学和声很难写的明白，也很难做到百分之百判断准确，不知道和声之前，可以去看乐谱的结束音（最后一个音）是什么，如下图，结束音是F那就是F大调，结束音是d就是d小调，如果中途有转调的话这个方法就没法用了，对于全曲都是一个调的来说，看结束音是谁，至少有百分之八十的准确性，然后再看一下全曲的起始音如果和结束音一样，那准确率在百分之九十左右，如果起始音和结束音不一样，那就看结束音

总结：

同主音调：

同主音调的同主音就是主音必须相同，如下图以C为主音的调式，只要主音一样那就是互为同主音调

以D为主音的调式

如果仅仅只说大调与小调这两种调式的话，可以把同主音调称为同主音大小调

关系大小调与同主音调在创作中实际运用与技巧需要学和声

平行大小调的歧义：

我们的音乐理论有很大一部分是从前苏联传过来的，前苏联的教材翻译成中文的平行大小调指的是现代的关系大小调，在我们国家平行大小调这个词，百分之九十五的人都会认为就是关系大小调，其它的人接触到的是欧美的教材，欧美教材翻译成中文的平行大小调指的是同主音大小调，因为它们是用parallel这个词来表示同主音大小调的，这个英文有平行的意思，所以从教材翻译的问题导致中文意义上有一些歧义