1236. 递增三元组：做题笔记

本文主要是介绍1236. 递增三元组：做题笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

暴力

代码

二分

代码

前缀和

代码

推荐视频讲解

暴力

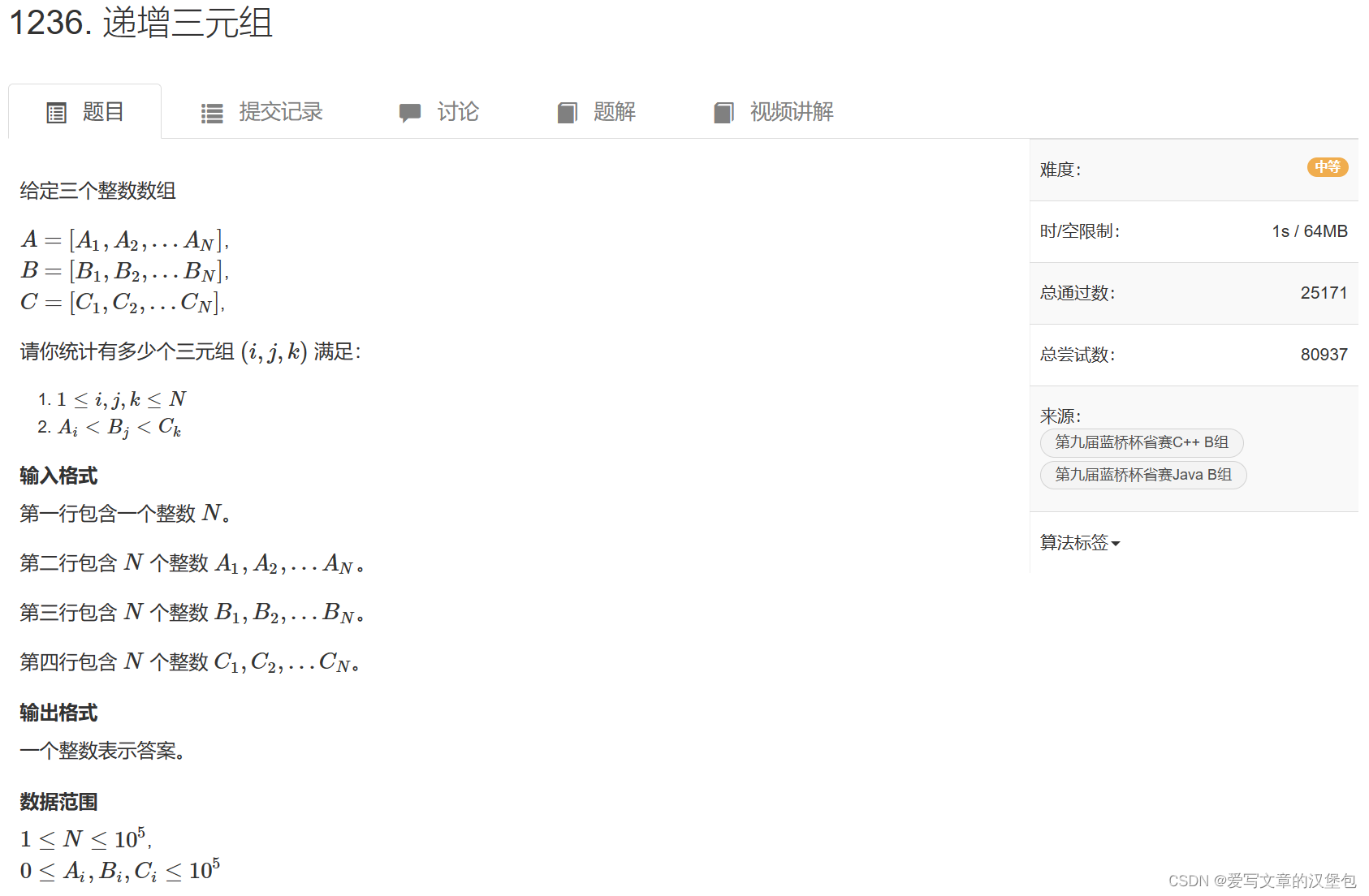
这道题说的是有三个元素数量相同的数组，想知道有多少个三元组满足：三个数分别来自 A B C数组且呈现递增。

我想的是既然要求递增，那就先把数组数据都排一下序，直接sort函数用起来。因为排了序的话就说明在某个数之后的所有数都是满足条件的，直接进行累加就可以。

第一个数A数组肯定要先遍历一下的(是的我当时做的时候压根没想到其他的)，我就想着我们既然想利用排完序的好处，那就从这想。

在第一层循环的基础上，在对第二层数据挑选的时候，就可以利用二分找到我们上面所说的“某个数”，这里的某个数其实也就是当前B数组里第一个大于当前外层循环正在处理的A数组的这个元素，我们知道在这个数之后的B数组中的数都是一种选择的可能。同理，到了最内层对从C数组中选的第三个数的可能性也就是在前两个数确定的这种情况下满足条件的可能性。

这样就枚举了所有可能性，肯定超时的。且这样的写法一个数据都过不了呜呜😭

我就没想到到底怎么优化掉第二层循环，，

代码

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=1e5+10;
int a[N],b[N],c[N],b1[N],c1[N];
int n;
int find(int q[],int x)
{int l=0,r=n;while(l<r){int mid=(l+r)/2;if(q[mid]>x)r=mid-1;else l=mid;}if(q[l]>x)return l;else if(q[l]==x)return l+1;else return -1;
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=0;i<n;i++)cin>>a[i];for(int i=0;i<n;i++)cin>>b[i];for(int i=0;i<n;i++)cin>>c[i];sort(a, a+n);sort(b, b+n);sort(c, c+n);int cnt=0;for(int i=0;i<n;i++){for(int j=find(b,a[i]);j<n;j++){//第三层循环还是好优化的(不过没什么卵用，因为双层循环仍然tle😜)/*for(int k=find(c,b[j]);k<n && k!=-1;k++){cnt++;}*/int k=find(c,b[j]);cnt+=n-k;}}cout<<cnt;return 0;}

二分

就是看了讲解才知道我们想降成一层循环，那留下来的这层循环就必须是中间的B数组。

因为A B C 三元组想递增嘛，那 A<B,C>B。遍历B数组每个元素，可以通过二分找到A数组中第一个大于当前B数组中元素的数的位置，和C数组中第一个大于当前B数组中元素的数的位置，通过元素总数与该位置的相减，得到其中间的元素个数。

我们可以写二分模板，也可以使用 lower_bound和upper_bound 函数，感觉直接用函数很方便。就像那个sort函数一样。

由于这两个函数的操作对象应该是有序的，我们需要对数组进行排序。

补充一下这两个函数的用法：

lower_bound(begin, end, value)：在从小到大排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个大于或等于value的数，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound(begin, end, value)：在从小到大排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个大于value的数，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

这两个函数的时间复杂度都是O(logN)，其中N是搜索空间中的元素数量。

代码

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=1e5+10;
int a[N],b[N],c[N];
int n;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=0;i<n;i++)cin>>a[i];for(int i=0;i<n;i++)cin>>b[i];for(int i=0;i<n;i++)cin>>c[i];sort(a, a+n);sort(b, b+n);sort(c, c+n);int cnt=0;for(int i=0;i<n;i++){int l=lower_bound(a,a+n,b[i])-a,r=n-(upper_bound(c,c+n,b[i])-c);cnt+=l*r;}cout<<cnt;return 0;}

l 是数组 a 中小于 b[i] 的元素的数量，r 是数组 c 中大于 b[i] 的元素的数量。

前缀和

这里前缀和的思路也是以B数组的遍历为主。

记录下所有数字出现的次数，预处理出前缀和，对A C数组进行排序，与B数组当前处理的元素进行比较，通过前缀和的运算得到A数组小于当前元素的个数，和C数组大于当前元素的个数，将这两个数相乘，并随着B数组的遍历对每一种情况进行累加得到最终结果。

关于前缀和的运算：A数组想得到小于当前元素的个数，直接b[i]-1的前缀和得到的就是想要的区间的前缀和 ( sa[b[i]-1] )

C数组想得到大于当前元素的个数，用 N 处的前缀和减去b[i]当前元素的前缀和即可( sc[N]-sc[b[i]] )

需要注意的是，由于数组中每个元素的数据范围是0-1e5，因此在前缀和计算中要从0开始，循环1e5次，关于数组越界问题：

代码

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=1e5+10;
int a[N],b[N],c[N];
int a1[N],c1[N];//存放每个数出现次数
int sa[N],sc[N];//计算a1,c1的前缀和
int as[N],cs[N];//通过前缀和的运算处理出所有可能的情况
//as代表比b[i]小的数的个数  cs代表比b[i]大的数的个数
int n;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=0;i<n;i++)cin>>a[i];for(int i=0;i<n;i++)cin>>b[i];for(int i=0;i<n;i++)cin>>c[i];for(int i=0;i<n;i++)a1[a[i]]++;for(int i=0;i<=N;i++)sa[i]=sa[i-1]+a1[i];for(int i=0;i<n;i++)as[i]=sa[b[i]-1];for(int i=0;i<n;i++)c1[c[i]]++;for(int i=0;i<=N;i++)sc[i]=sc[i-1]+c1[i];for(int i=0;i<n;i++)cs[i]=sc[N]-sc[b[i]];int cnt=0;for(int i=0;i<n;i++){cnt+=as[i]*cs[i];}cout<<cnt;return 0;}