本文主要是介绍【博弈论——2探究纳什均衡】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.纳什均衡
纳什均衡(Nash Equilibrium),由美国数学家约翰·纳什(John Nash)提出,是博弈论中的一个重要概念,用来描述在一个非合作博弈中,各个参与者在考虑了其他所有参与者策略的前提下,找不到单方面改变自己策略就能增加自己收益的动机时所形成的一种相对稳定的策略组合状态。
具体来说,如果在一场博弈中,每个参与者都选择了自己的最优策略,而且这些策略形成了一个组合,在这个策略组合下,任何一个参与者若单独改变其策略,其收益都不会提高,则称这种策略组合为一个纳什均衡点。这意味着,在纳什均衡状态下,没有任何一个参与者有动机偏离当前的策略选择。
例如,在著名的“囚徒困境”博弈中,存在一个纳什均衡,即两个囚犯都选择背叛对方,尽管从全局角度来看,如果双方都能信任对方并合作保持沉默,他们的总刑期会更短,但由于信息不对称和个体理性的驱使,最终形成的均衡就是两者都背叛。
1.1 占优策略
占优策略(Dominant Strategy)是博弈论中的核心概念之一,指的是在博弈中,某个参与者不论其他参与者选择何种策略,选择该策略始终对自己是最优的。换言之,即使不知道对手的具体策略,只要采用占优策略,参与者就可以保证自己的结果不会因为对手的选择而变得更差。
不过,并非所有的博弈都存在占优策略。在很多情况下,参与者需要根据对手可能的选择进行复杂的分析才能找到最优策略。
1.2 占优策略均衡
占优策略均衡(Dominant Strategy Equilibrium)是博弈论中的一个概念,它是指在一个博弈中,每个参与者都拥有各自的占优策略,并且当所有参与者都遵循这些占优策略时,整个博弈达到一种均衡状态。
1.3 纳什均衡
同上
1.4 合作均衡
合作均衡强调的是博弈参与者之间通过某种形式的合作(如签订合约或形成联盟)来提高整体的效益,而不是单纯追求个体利益最大化。一个博弈达到合作均衡意味着参与者组成的联盟达成了一个契约,使得没有人愿意脱离这个联盟去寻求更高的收益,也就是说,在契约约束下,所有参与者都能接受并且执行约定的策略组合,这样整体的效益相较于无组织的合作或非合作博弈状态更高。
在合作博弈论中,合作均衡的一个重要概念是核(Core),它代表了一个契约集合,使得任何联盟都不具备动力去破坏这个契约另起炉灶,即留在原契约中的收益大于任何可能的拆分联盟的收益分配。
另外,还有像夏普利值(Shapley value)和贝叶斯谈判解决方案(Bargaining Solution)等方法来衡量和分配合作博弈中的收益,这些也可以导致合作均衡的达成。
2. 烟草广告博弈
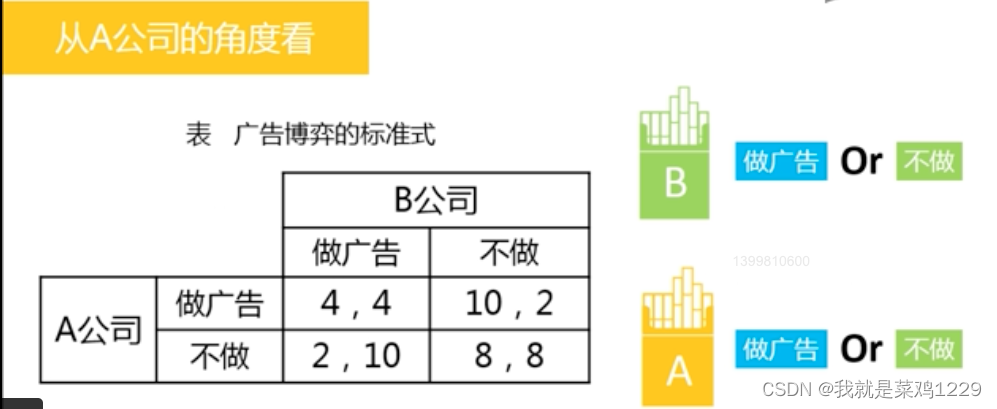
做广告是占优策略。
占优测量均衡为(做广告,做广告)
合作均衡(不做广告,不做广告),这个合作均衡需要外界强有力的干预。
3. 不存在占优策略的博弈
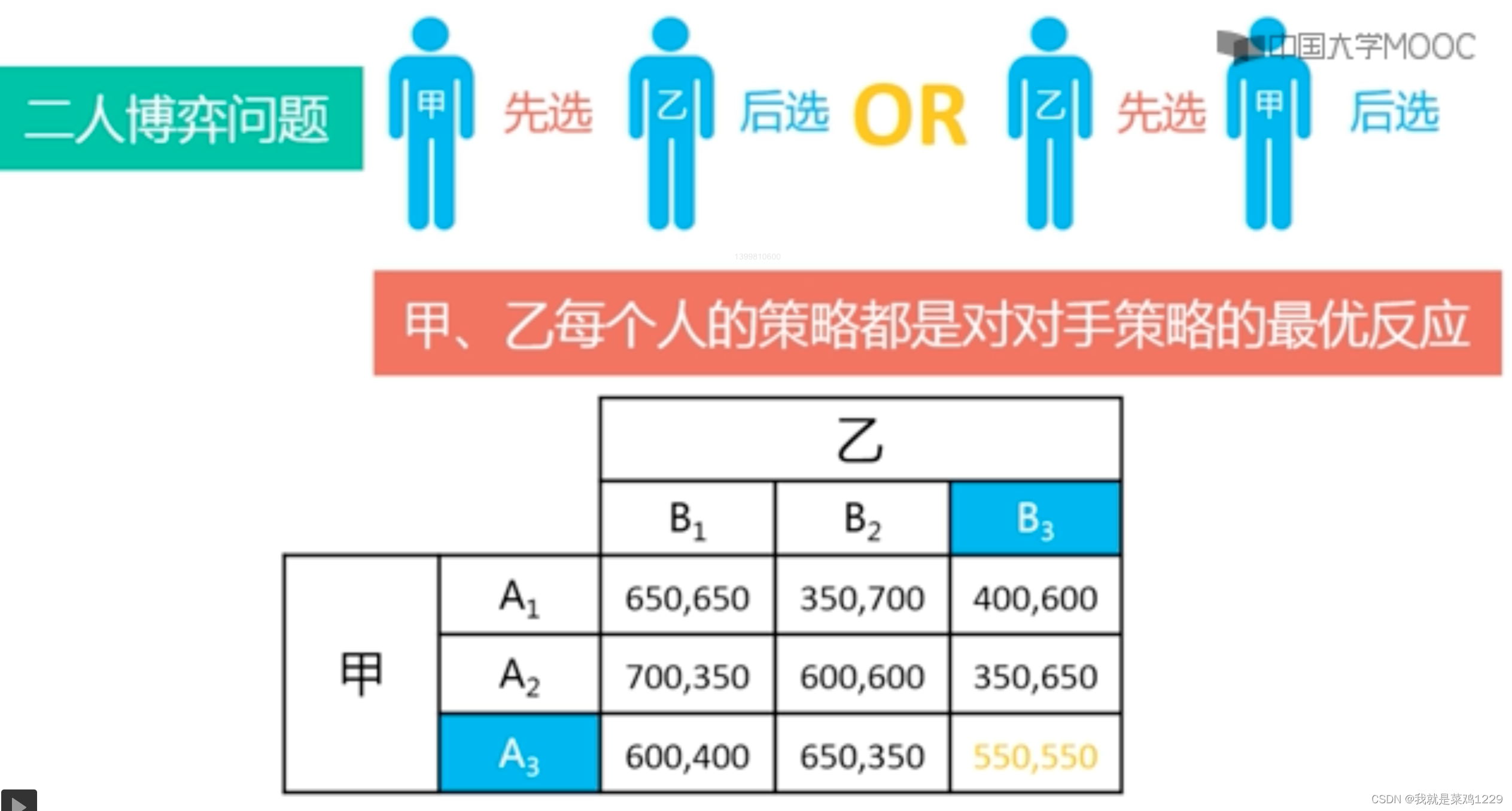
4. 非合作博弈几种均衡概念之间关系
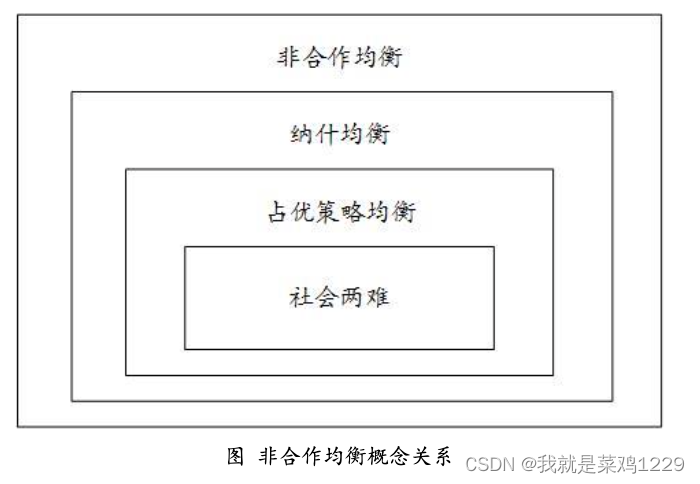
5. 如何寻找纳什均衡
划线法:将收益矩阵中与每一策略的最优反应策略相对应的收益数字标注下划线,如果一个方框中的两个数字都被标注了下划线,这个方框对应的策略组合就上该博弈的一个纳什均衡。
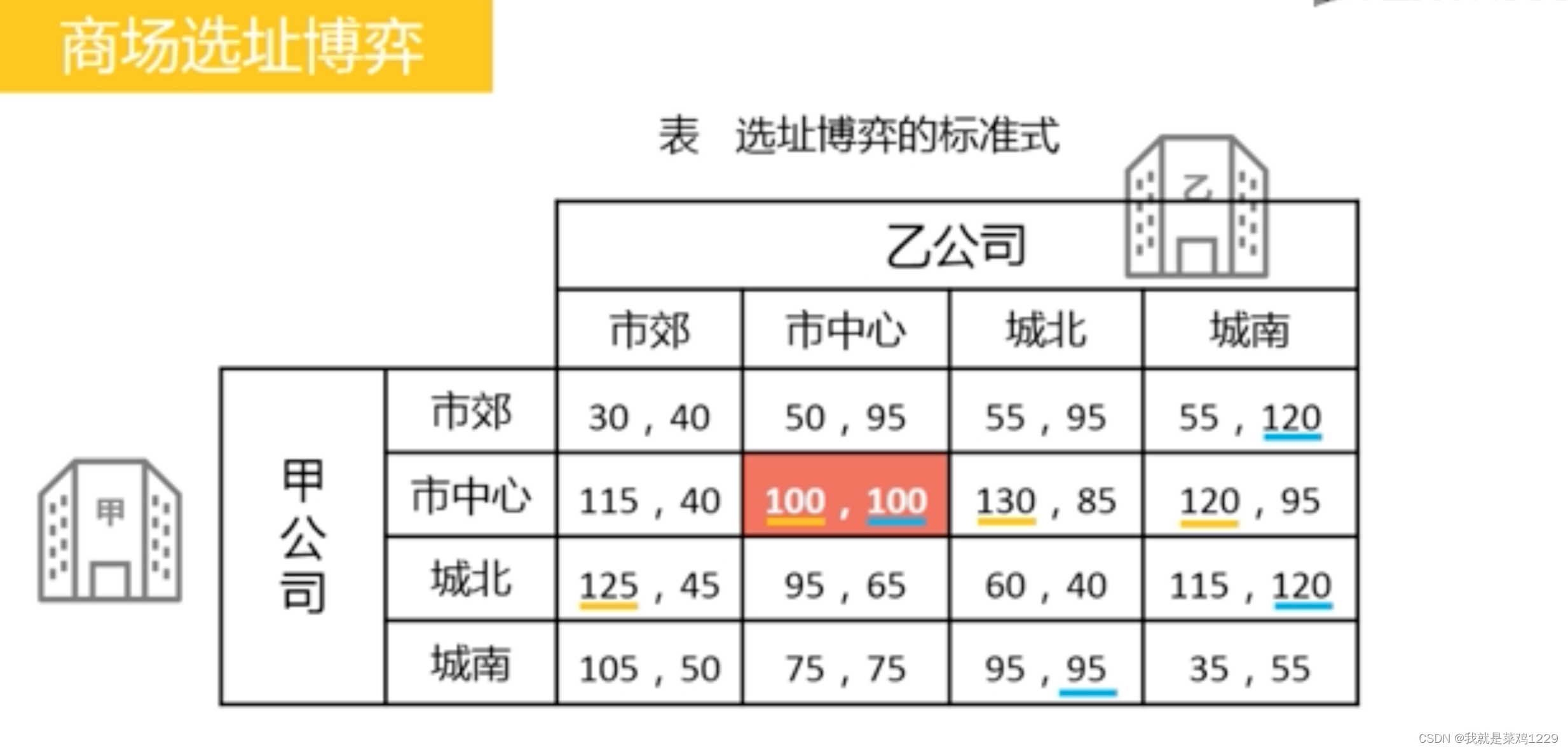
6.多重纳什均衡
当一局博弈存在两个或两个以上的纳什均衡,我们就称这句博弈存在多重纳什均衡。
对于那些有多个纳什均衡存在的博弈而言,我们无法肯定地证明这个博弈的纳什均衡一定会出现,这也是博弈分析中真正的难题,通常称这个问题为“纳什均衡的多重性问题”。
解决方案()
- 聚点均衡
- 帕累托最优标准
- 风险优势标准
- 相关均衡
- 子博弈完美均衡
- 抗共谋均衡
- 颤抖手完美均衡

7.谢林点
谢林点(Schelling Point)是由美国经济学家托马斯·谢林(Thomas Schelling)在其1960年的著作《冲突的战略》(The Strategy of Conflict)中提出的概念。在博弈论中,谢林点指的是在缺乏充分沟通或信息的情况下,人们倾向于选择的、基于某些共同预期或显著特征的策略或行动点。它是一个“聚焦点”,是参与者们在不明确的情况下可能会自然而然地聚集到一起的决策位置。
- 在特定情况下,惯例和传统能够帮助我们确定博弈的多重纳什均衡中哪个更可能出现
- 协调博弈中的纳什均衡可以解释:为什么习俗和管理看似很随意,实际却很稳定,因为它们都是纳什均衡,能够自我强化。
8.双寡头市场结构的古诺模型
古诺模型是“囚徒博弈”的变种
在古诺模型中,假设有两个完全相同的厂商,它们生产同质产品并在市场上进行竞争。每个厂商面临以下特点:
- 成本函数:厂商生产的边际成本(marginal cost)是常数,表示每增加一单位产品的生产所带来的额外成本不变,记为 c。
- 市场需求:市场需求曲线是线性的,总市场的需求量 Q 会随着市场价格 p 下降而上升,可表达为 P = a - bQ,其中 a 表示市场需求的价格弹性系数,b 表示需求的价格敏感度。
- 产量决策:每个厂商独立决定自己的产量 q1 和 q2,但它们都知道对方也会做同样的决策。
- 市场竞争:价格由市场上的总供应量决定,即总供应量等于两个厂商的产量之和,即 P = c + (a - bq1 - bq2) / 2,其中市场的总需求减去总供给后除以2是因为假定厂商把市场分割平均。
每个厂商的目标是最大化自己的利润,利润函数可以表示为 πi = P * qi - c * qi,其中 i∈{1,2} 表示厂商编号。
在古诺模型中,每个厂商通过计算自身的反应函数(best response function)来确定最优产量,即在已知竞争对手产量的情况下,寻找能使自己利润最大的产量水平。最终的均衡状态是两个厂商分别确定的产量水平,这两个产量水平构成了一个纳什均衡,即在给定对方产量的情况下,没有厂商愿意单独改变自己的产量。
在均衡状态下,每个厂商的产量都不是无限大,而是低于完全竞争条件下厂商会提供的产量,这是因为厂商考虑到增加产量会导致市场价格下降,从而减少每单位产品的利润。因此,古诺模型显示了寡头市场中,厂商之间的相互依赖性如何影响市场产量和价格。
这篇关于【博弈论——2探究纳什均衡】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







