本文主要是介绍代码随想录算法训练营第二十四天|回溯算法基础理论, 77. 组合,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
回溯法
什么是回溯法?
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
回溯是递归的副产品,只要有递归就会有回溯。
回溯位于递归的下方。
回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案(纯暴力的搜索)。
回溯法解决的问题
回溯法,一般可以解决如下几种问题:
1、组合问题:N个数里面按一定规则找出k个数的集合;
2、切割问题:一个字符串按一定规则有几种切割方式;
3、子集问题:一个N个数的集合里有多少符合条件的子集;
4、排列问题:N个数按一定规则全排列,有几种排列方式;
5、棋盘问题:N皇后,解数独等等。
注意:组合是不强调元素顺序的,排列是强调元素顺序
如何理解回溯法
回溯法都可以抽象为一个树形结构。
因为回溯法解决的都是在集合中递归查找子集,集合的大小构成了树的宽度,递归的深度构成了树的深度。
回溯法的模板
1、回溯法函数的参数和返回值
一般返回值为void,参数可能较多,可以在后续使用中随时更新参数,基本形式如下:
void backtracking(参数)
2、回溯函数的终止条件
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
if (终止条件) {存放结果;return;
}
3、回溯函数单层搜索的逻辑
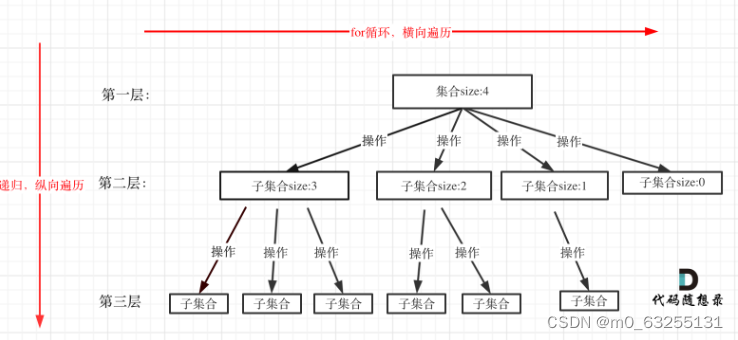
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次
总结,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
题目:77.组合
给定两个整数 n 和 k,返回范围[1, n]中所有可能的 k 个数的组合。
你可以按任何顺序返回答案。

题目链接/文章讲解:https://programmercarl.com/0077.%E7%BB%84%E5%90%88.html
视频讲解:https://www.bilibili.com/video/BV1ti4y1L7cv
剪枝操作:https://www.bilibili.com/video/BV1wi4y157er
思路
把组合问题抽象成树形结构:

树的叶子节点就是要的结果
解题
class Solution {
private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {result.clear(); // 可以不写path.clear(); // 可以不写backtracking(n, k, 1);return result;}
};
对组合回溯进行剪枝
去重多余的搜索操作
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方path.push_back(i); // 处理节点backtracking(n, k, i + 1);path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};
这篇关于代码随想录算法训练营第二十四天|回溯算法基础理论, 77. 组合的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





