【算法】活用双指针完成--字符串相乘（双指针，图例详解！！！）

本文主要是介绍【算法】活用双指针完成--字符串相乘（双指针，图例详解！！！），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、前言

二、字符串相乘

✨方法一：普通竖式法

✨方法二：优化竖式法

三、共勉

一、前言

最近春招已经开始，看周围的同学都在投递一些大厂的实习，某为的手撕代码 --- 字符串相乘，某讯的手撕代码 --- 字符串相减等。

于是专门去 Leetcode 上搜索了一下，发现这类题目是面试常考的题目。只要我们熟练的 掌握四则运算，熟练的掌握字符串的处理，就可以迎刃而解啦！

常考算法面试题分为：字符串（大数）相加、字符串（大数）相乘、字符串（大数）相减。本次博客主要通过图例和双指针来讲解 ---- 字符串（大数）相乘
如果想看字符串相乘可以看这篇文章：字符串相加

二、字符串相乘

题目链接： 43. 字符串相乘 - 力扣（LeetCode）

题目分析：

✨方法一：普通竖式法

该方法基于我们平常的乘法运算，我们一般在草稿纸上列竖式，用乘数的每一位分别乘以被乘数，然后将这些结果加起来得到最终结果，只不过要注意的是：用乘数的各个位与被乘数相乘所得到的这些数在相加时，需要错位相加。

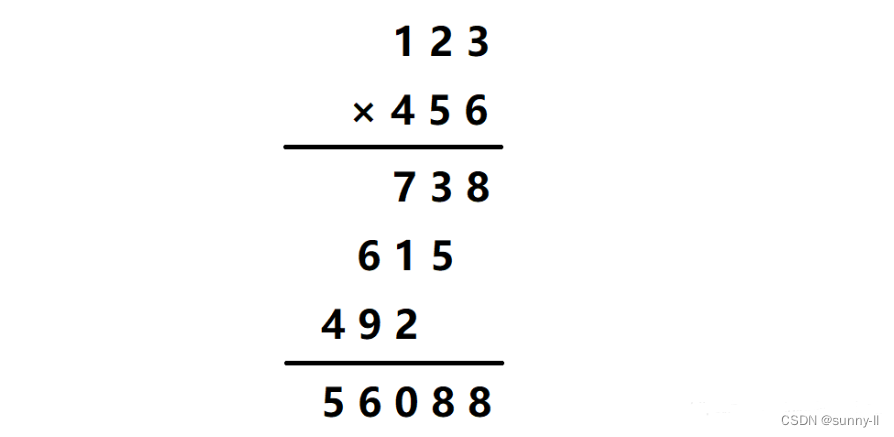
实际上我们可以将这些错位看成是在数字的后面添上了数字0，这样一来就有规律可循了。在乘数的最后一位（个位）与被乘数相乘的结果后面添上零个0，在乘数的倒数第二位（十位）与被乘数相乘的结果后面添上一个0，在乘数的倒数第三位（百位）与被乘数相乘的结果后面添上两个0，最后将这些结果相加就得到了最终结果。

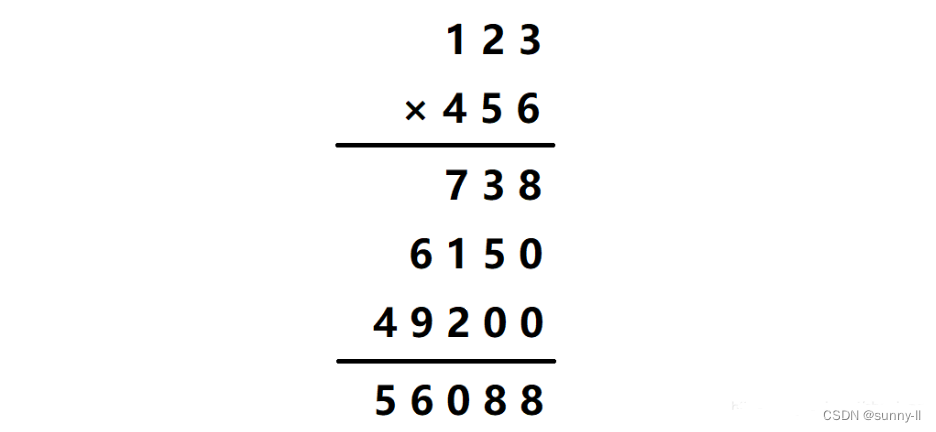
结论如下： 将乘数的每一位分别与被乘数相乘，并且在乘数的倒数第n位与被乘数相乘的结果后添上n-1个0，再将这些结果相加，即可得到最终结果。

class Solution {
public://字符串相乘string multiply(string num1, string num2) {if (num1 == "0" || num2 == "0")return "0";string retArr; //相乘后的字符串int flag = 0; //标识需要添加的0的个数for (int i = num2.size() - 1; i >= 0; i--) //依次取乘数的倒数第一位、倒数第二位、...{int count = num2[i] - '0'; //乘数当中待与被乘数相乘的那一位的数字string tmp; //存储乘数该位与被乘数相乘后的结果（此时为空）//数count与被乘数相乘，相当于将被乘数加count次到tmp当中for (int j = 0; j < count; j++){tmp = addStrings(tmp, num1);}//在字符串tmp后添上flag个0for (int k = 0; k < flag; k++)tmp.push_back('0');retArr = addStrings(retArr, tmp); //将字符串tmp加到结果字符串retArr当中flag++; //下一次tmp字符串后面需要添加的0的个数增加}return retArr; //返回相乘后的字符串}//字符串相加string addStrings(string s1, string s2) {int next = 0; //标识进位int end1 = s1.size() - 1, end2 = s2.size() - 1;string retArr; //相加后的字符串while (end1 >= 0 || end2 >= 0) //只要有一个字符串未遍历完毕就继续{int num1 = 0; //第一个字符串待相加的数字if (end1 >= 0){num1 = s1[end1] - '0';end1--;}int num2 = 0; //第二个字符串待相加的数字if (end2 >= 0){num2 = s2[end2] - '0';end2--;}int sum = num1 + num2 + next; //两个待相加数字相加后的结果（注意加上进位next）if (sum > 9) //需要进位{next = 1; //标识进位sum -= 10; //进位后该位置的数字}else //无需进位next = 0;retArr.push_back(sum + '0'); //尾插到结果字符串retArr当中}if (next == 1) //还需进位retArr.push_back('1'); //将字符1尾插到结果字符串retArr当中reverse(retArr.begin(), retArr.end()); //逆置字符串retArrreturn retArr; //返回相加后的字符串}
};

✨方法二：优化竖式法

方法一的做法是将乘数的每一位分别与被乘数相乘（实际上是将被乘数加若干次到空字符串当中），并且在乘数的倒数第n位与被乘数相乘的结果后添上n-1个0，再将这些结果字符串相加，从而得到最终结果。但是整个过程中涉及到较多字符串相加的操作，如果我们使用数组代替字符串存储结果，则可以减少对字符串的操作。

首先，我们取乘数的每一位分别与被乘数的每一位相乘，相乘的结果放在对应位置，但是不进行进位操作，后面统一进行。

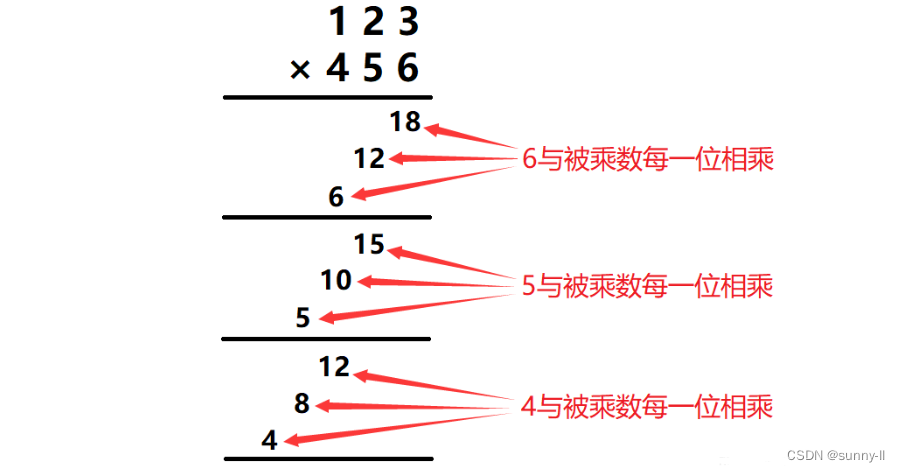
到这里先解决一个问题：数组arr应该开辟多大空间才足矣容纳这两个数的乘积？

我们假设被乘数num1的长度为m，乘数num2的长度为n，并且它们均不为0，那么它们乘积的长度为m+n-1或m+n。
证明如下：

如果num1和num2都取最小值，即 num1 = 10m-1，num2 = 10n-1，那么num1和num2的乘积就为10m+n-2，即乘积的长度为m+n-1。
如果num1和num2都取最大值，即num1 = 10m-1，num2 = 10n-1，那么num1和num2的乘积就为10m+n-10m-10n+1，该结果是小于10m+n而大于10m+n-1的，即乘积的长度为m+n。

综上所述：长度分别为m和n的数相乘后的乘积长度为m+n-1或m+n。

开辟可容纳6个元素的数组arr，然后将对应位置相同的结果相加，相加后的结果放在数组arr的对应位置。

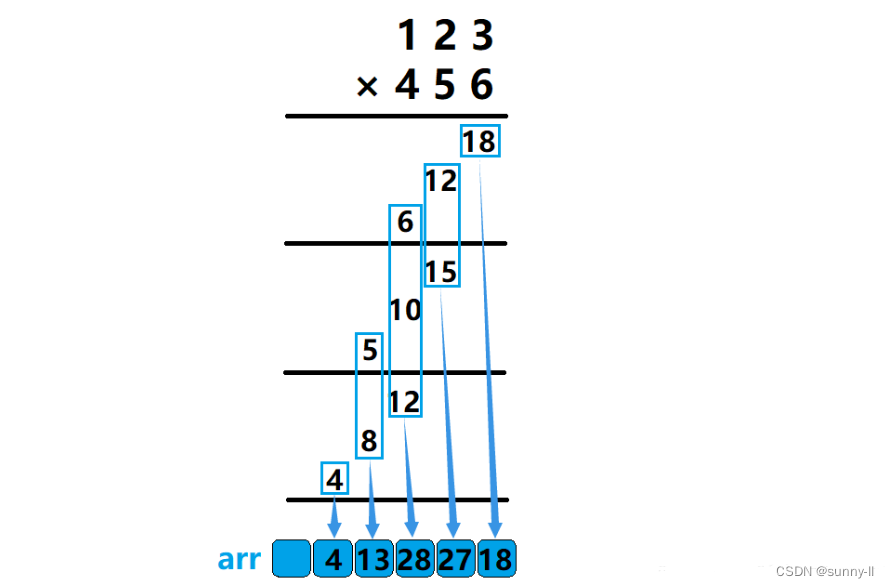
这里不需要在任何结果后面添0，那我们是如何做到将对应位置相加的结果放在数组arr的对应位置的呢？

稍作观察，我们可以发现其规律所在，我们只需要将乘数的第 i 位与被乘数的第 j 位相乘的结果加到数组arr中下标为 i+j+1 的位置即可。例如，乘数的5（第1位与）被乘数的3（第2位）相乘的结果应该加到数组arr中下标为4（1+2+1）的位置即可。

然后我们对数组arr当中的数据从后往前进行进位操作，最终数组当中的数据就是这两个数的乘积。

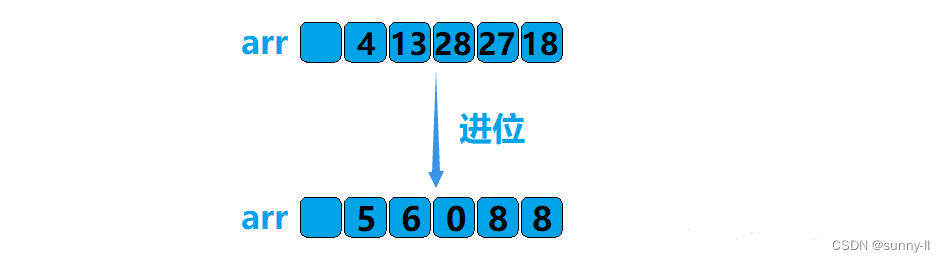
我们将数组当中的数一个个尾插到空字符串当中，该字符串当中存储的便是这两个数的乘积。但是我们应该从数组的第几个位置开始进行尾插呢？

我们默认从数组中下标为1的位置开始尾插，但如果通过判断发现数组arr当中下标为0的位置的数不为0，那么我们应该从数组当中下标为0的位置开始进行尾插。

class Solution {
public:string multiply(string num1, string num2) {if (num1 == "0" || num2 == "0")return "0";int m = num1.size(), n = num2.size();vector<int> arr(m + n, 0); //开辟数组arr的大小为m+n，并且全部初始化为0for (int i = n - 1; i >= 0; i--) //取乘数的每一位{int a = num2[i] - '0';for (int j = m - 1; j >= 0; j--) //取被乘数的每一位{int b = num1[j] - '0';arr[i + j + 1] += a*b; //乘数的第i位与被乘数的第j位相乘后的结果放在数组arr中下标为i+j+1的位置}}//从后往前对数组arr进行进位操作int end = m + n - 1;while (end > 0){arr[end - 1] += arr[end] / 10; //进位arr[end] %= 10; //当前位进位后的数end--; //从后往前进行迭代}int flag = 1; //默认有效值从数组arr当中下标为1的位置开始if (arr[0] != 0)flag = 0; //若数组arr当中下标为0的位置的数据不为0，则从第0位开始为有效数据string retArr; //相乘后的字符串//依次将数据尾插到字符串retArr当中for (int i = flag; i < m + n; i++){retArr.push_back(arr[i] + '0');}return retArr; //返回相乘后的字符串}
};