算法打卡day31|贪心算法篇05|Leetcode 435. 无重叠区间、763.划分字母区间、56. 合并区间

本文主要是介绍算法打卡day31|贪心算法篇05|Leetcode 435. 无重叠区间、763.划分字母区间、56. 合并区间，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

算法题

Leetcode 435. 无重叠区间

题目链接:435. 无重叠区间

大佬视频讲解：无重叠区间视频讲解

个人思路

和昨日的最少箭扎气球有些类似，先按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了

解法

贪心法

首先区间1，2，3，4，5，6都按照右边界排好序。

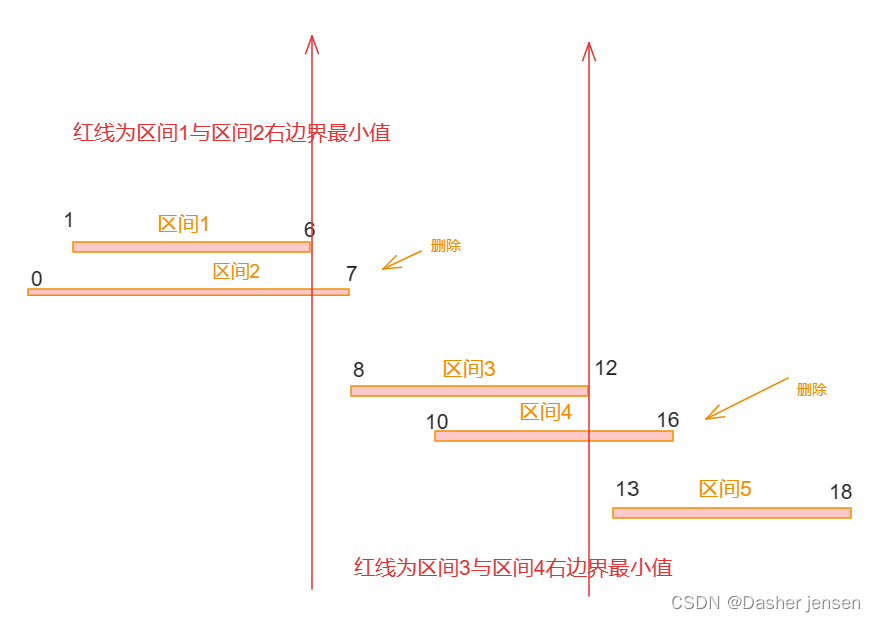
取区间1 右边界a和区间2左边界b，如果区间a>b时，说明区间交叉，需要删除一个重叠区间，重新找右边界，取区间a和b中的最小右边界，继续往后遍历。若a<b，说明区间不交叉，数量加1.

总共区间个数为5，减去非交叉区间的个数3,移除区间的最小数量就是2。

class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals, (a,b)-> {//按右边界排序return Integer.compare(a[0],b[0]);});int count = 1;for(int i = 1;i < intervals.length;i++){if(intervals[i][0] < intervals[i-1][1]){intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);//选择小的右边continue;}else{count++;//非交叉区间数加1}    }return intervals.length - count;//需要删除的区间数}
}

时间复杂度:O(n logN)；（排序数组）

空间复杂度:O( logN);（java所使用的内置函数用的是快速排序需要 logN 的空间）

Leetcode 763.划分字母区间

题目链接:763.划分字母区间

大佬视频讲解：划分字母区间视频讲解

个人思路

这道题有些技巧，但这个技巧我不知道...

解法

贪心法

在遍历的过程中相当于是要找每一个字母的边界，当找到之前遍历过的所有字母的最远边界，也就找到了分割点。此时前面出现过所有字母，最远也就到这个边界了。

所以步骤为

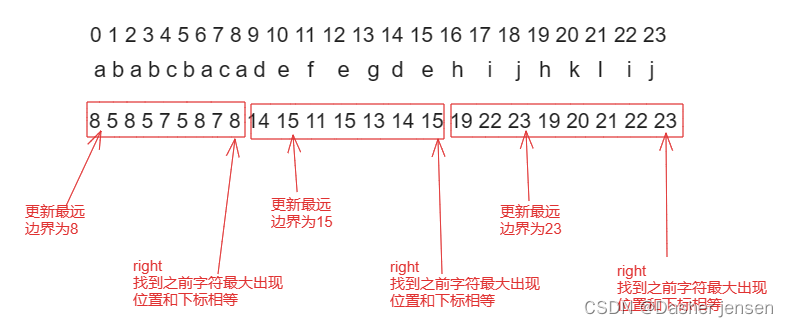
统计每一个字符最后出现的位置
从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

class Solution {public List<Integer> partitionLabels(String S) {List<Integer> list = new LinkedList<>();int[] edge = new int[26];//边界数组char[] chars = S.toCharArray();//字符串转字符串数组for (int i = 0; i < chars.length; i++) {//更新字母的最远边界edge[chars[i] - 'a'] = i;}int idx = 0;int last = -1;for (int i = 0; i < chars.length; i++) {//遍历数组idx = Math.max(idx,edge[chars[i] - 'a']);if (i == idx) {//找到最远边界后分割，收集字符串长度list.add(i - last);last = i;}}return list;}
}

时间复杂度:O(n )；（遍历数组）

空间复杂度:O(1);（hash数组是固定大小）

Leetcode 56. 合并区间

题目链接:56. 合并区间

大佬视频讲解：合并区间视频讲解

个人思路

这道题和无重叠区间，最少箭射气球，都是判断区间重叠。区别就是判断区间重叠后的逻辑，这道题是判断区间重叠后要进行区间合并，因此还是贪心，先排序再处理。

解法

贪心法

先拿题目例子画个图 intervals = [[1,3],[2,6],[8,10],[15,18]]

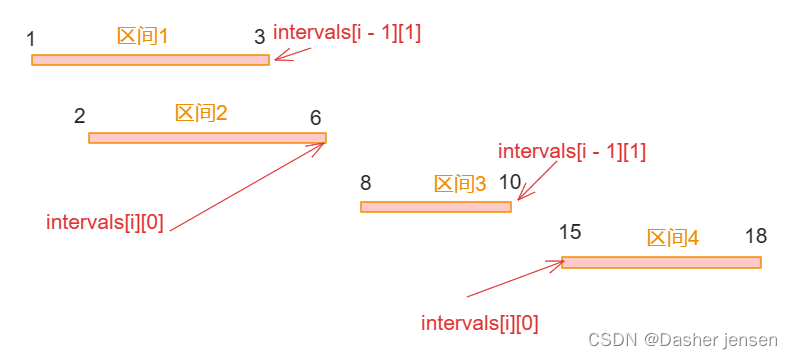
先按照左边界从小到大排序，然后如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重爹，所以是<=）

将重叠区间合并，合并后取最小左边界和最大右边界，作为一个新的区间，加入到result数组。如果没有合并就把原区间加入到result数组。


class Solution {public int[][] merge(int[][] intervals) {List<int[]> res = new LinkedList<>();Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));//按照左边界排序int start = intervals[0][0];//最小左边界int rightmost= intervals[0][1];//最大右边界for (int i = 1; i < intervals.length; i++) {//如果左边界大于最大右边界if (intervals[i][0] > rightmost) {res.add(new int[]{start, rightmost});//加入区间start = intervals[i][0];//更新startrightmost= intervals[i][1];} else {rightmost= Math.max(rightmost, intervals[i][1]);//更新最大右边界}}res.add(new int[]{start, rightmost});return res.toArray(new int[res.size()][]);}
}