本文主要是介绍【蓝桥杯】 第九届国赛 第四题 测试次数(动态规划),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第九届国赛 第四题 测试次数
问题描述
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。某次测试的塔高为1000层,如果我们总是采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数。
注意:需要填写的是一个整数,不要填写任何多余内容。
---分割线---
思路一(编程角度):
首先需要注意:本题中的手机是没有后效性的,即:没有扔坏的话可以当作新的继续扔
然后这道题明显存在着某种递归关系
仔细看题目中很关键的一句话“总是采用最佳策略,在最坏的运气下最多需要测试多少次”
好了,看到这句话基本可以确定的是这是一个dp(动态规划)
那么我们需要先确定一下dp的元素:楼层数、手机数
一. 根据变量制表:
图中白色空格中内容为(仅有i层楼时利用j个手机在最佳策略但运气最坏下的)摔手机次数
表格中红色部分即为题目要求解,数量过大不可能人脑推算,只能编程,为此我们先人工填表找规律
对应数据结构就是一个二维数组:int dp[1001][4] (从1开始)
二.完善表格:
- 手机数量为1时:
在手机仅有一个时,为了保证能够测试出耐摔指数就只能一层一层的摔,所以有几层就要摔几次,并且测试方法只能是从第一层楼逐渐往上摔,直到手机摔碎或者到顶。即第一行的表格只能填写为:

对应代码如下:
for(int i = 1 ; i<=1000 ; i++)dp[i][1] = i;
- 手机数量为2时:
1层楼时,情况和手机数为1时一致(均为1)。
2层楼时,由于总是遇到最坏的运气,何谓最坏的运气?这么给你解释吧,现在两层楼两个手机让你测试耐摔指数。你有两个方案:
1.先从1楼开始测试;
2.先从2楼开始测试(注意:这里是因为总楼层低(只有2层)你才可以从2楼先扔,要是楼层高了,你从大于2的楼层开始扔是不能保证能测试出手机的耐摔指数的,换言之这里(楼层数<=2)你先从2楼扔是一种特殊情形)
现在假设从1楼开始测试,由于你运气不好,那么意思就是你还要再测试一次(也就是说在1楼扔下去没有摔坏,你还需要再去2楼测试一次)。至于最后的结果如何我们不关心,总之你需要测试两次
同样地,假设现在你从2楼开始测试,那么由于运气不好,同样地你也要再测试一次(也就是说在2楼扔下去摔坏了,那么你需要换另一个手机再去1楼测试一次)。同样地这之后的结果如何我们不关心,反正总的你要测试两次。
总结看来,这个最坏的运气就是指你总是在往着测试次数更多的方向发展。
于是通过以上分析可以先得到以下表:

这时候来看当存在3楼时的情况
首先要知道,前面2部手机2层楼时,是一定可以保证你能得到手机的耐摔指数的
现在是2部手机3层楼,那么我们是可以在前面的结论的基础上进行测试的
也就是说,假设前面先测试第1层楼,运气最坏嘛,那就要继续测试,也就是说在1楼没坏,那接着测试第2层楼;同样地,运气最坏嘛,那就不能坏,继续摔,于是接着测试第3层楼。共3次。
显然,上面的这个分析给出了一个关系:
当多一层楼时,dp[i][j]总是存在一个最差关系,即dp[i][j]=dp[i-1][j]+1(反正前面楼的测试结果为dp[i-1][j]嘛,那么现在多一层楼,我最差的情况也就仅仅比这个情况多测试一次(因为最坏运气的原因,必定让你再多上一层楼),即dp[i][j]=dp[i-1][j]+1),也就是说3楼2手机的空格位置处可以填的最大值为3,那么最小值呢?
实际上,我们知道当多一层楼时,也许会有一个更优的方案(有这种可能,但也可能没有)
比如现在(接着这个情况分析:2部手机3层楼),由于我有两部手机,那我可以冒险一点不用一层一层的扔。之前必须一层一层的扔是因为当时只有一部手机,如果你不一层一层扔,那么当某次扔下去坏了,而你又是从中间某个位置扔的,那么你就不知道手机的耐摔指数到底是多少。(比如50层楼,你从25层扔下去,摔坏了,那你也不知道这个手机的耐摔指数是多少了)。因此必须一层一层扔。
可现在你有两部手机,那么情况就不一样了:你是可以从中间某个位置去扔以降低测试次数。
现在的问题便是,从中间哪个位置才合适呢?
你想,为了让你发挥出具有两个手机的优势,你一定会存在的保障是:当第一部手机摔坏了,此时第二部手机能够从刚才摔坏的位置继续执行任务。不同的是,这一次你必须保证能测试出其耐摔指数。那么这时你仅剩下一部手机,不是和之前只有一部手机时的情况如出一辙么?也就是只能一层一层的测试了。
那也就是说,当你有两部手机时,每次测试时你只需保证与已经测试了的楼层有2层楼的间隔,以保证当这一次摔坏了,只剩下中间一层时,你仍然能完成测试任务(这时你只需要测试中间这一楼就一定可测出)。这也就是我们所采用的最优策略了。
回到3层楼这里(2部手机),那么我们就直接测试第2层楼
如果坏了,那么我们就测试1楼,共测试两次(不关心最后测试坏还是没坏,反正能得出总的测试结果)
如果没坏,那么我们就测试3楼,共测试两次(不关心最后测试坏还是没坏,反正能得出总的测试结果)
于是可以得到以下表格:

三.总结规律:
①每个空的最大值(即保证每个空至少能有一个测试次数,不至于空着没答案):由于我们可以确定每个空的最大值为其前一楼层次数+1(例如:求2个手机,3层楼时的测试次数时,在已测试出了两层楼的测试次数的前提下,在3楼再摔一次一定可以得到3楼的次数) 即 每个dp[i][j]的最大值总是满足dp[i][j]= dp[i-1][j]+1
②每个空的最优值(也许会和最大值相等):当采用最优策略时(在中间某层(设为k)扔)会有两种情况:
1.损坏:说明楼层过高,接下来应尝试当前层下面的k-1层,但手机数-1: dp[i][j]=dp[k-1][j-1]+1
2.未损坏:说明楼层不够高,接下来应尝试当前层上面共n-k层(假设总楼层数为n),此时手机数没变:dp[i][j]=dp[n-k][j]+1
这时候,到底选那种情况呢?题目说了:总是遇到最坏的运气!
而前面我也说了,最坏的运气,在我们的程序中体现为接下来测试的次数会更多。
即我们的代码应该是:dp[i][j] = max(损坏,未损坏)= max(dp[k-1][j-1]+1,dp[n-k][i]+1)
这也就是我们的递推式子了
下面给出本题完整代码:
#include<iostream>
using namespace std;
int main()
{int dp[1010][5]={0}; //dp[i][j]:在仅有i层楼时使用j个手机需要摔的最大次数for(int i=1;i<=1000;i++) //只有一个手机时,几层楼就要摔几次(确保能测出耐摔指数)dp[i][1]=i;for(int i=2;i<=3;i++)for(int j=1;j<=1000;j++){dp[j][i]=dp[j-1][i]+1; //赋最大初值(楼层每增加一层,其需要摔的次数一定会小于等于其楼层数减一的次数+1) for(int k=2;k<j;k++) //最优策略(在中间楼层逐个寻找,以找到测试次数最多的那个)dp[j][i]=min(dp[j][i],max(dp[k-1][i-1],dp[j-k][i])+1);//外部的min表示着采用最优策略,而内部的max则是指每一个最优策略都是在受到最坏运气的影响下得到}cout<<dp[1000][3]<<endl;return 0;}
思路二(纯数学角度):
参考自博客:https://blog.csdn.net/nka_kun/article/details/79789511
要知道这是一道填空题,无论什么手段,只要能得到答案就行!!!
这种具有很浓烈的数学味道的题(况且还是填空题),大多数情况下,我们的第一反应都应该是想能不能以纯数学的方法来求解。
在分析这道题之前,我们先引入一个100层楼扔两个鸡蛋的问题
两个软硬程度一样但未知的鸡蛋,它们有可能都在一楼就摔碎,也可能从一百层楼摔下来没事
有座100层的建筑,要你用这两个鸡蛋确定哪一层是鸡蛋可以安全落下的最高位置。可以摔碎两个鸡蛋
最少需要几次测试,才能得到摔碎鸡蛋的楼层?方案如何?
对这个问题,原始问题——【两个鸡蛋100层楼,最少需要几次测试,才能得到摔碎鸡蛋的楼层】
直接考虑不容易考虑,但是,如果将这个问题进行一种等价的转换,这个问题将会变得非常容易解答。
个人认为,这个转换是解决这个问题的核心,这个转换是:
转换问题——【两个鸡蛋,进行k次测试,最多可以测试几层楼】
如果大家能想到将“原始问题”变为“转换问题”,其实就已经解决了一半
现在我们以“转换问题”为模板进行考虑,有两个鸡蛋,第一个鸡蛋如果破碎,第二个鸡蛋就必须只能一层一层的测试了,并且我们要求,进行k次测试就一定能将摔碎鸡蛋的楼层找到
考虑第一次测试。第一次测试的时候,第一个鸡蛋放置的楼层不能太高了,否则,如果第一个鸡蛋破碎,第二个鸡蛋可能不能在k次测试后得到结果。但是也不能放置的矮了,因为如果放置的矮了,第一个鸡蛋破碎了还好说,如果没破,我们浪费了一次测试机会,也不能说是完全浪费了,不过至少是让效用没有最大化。所以,第一次测试的时候必须让第一个鸡蛋的放置位置不高不矮。
不高不矮是多高?
高到如果第一个鸡蛋破碎后,第二个鸡蛋刚好能在剩下的k-1次中将这剩余的楼层数量测试出。由此可知,第一次测试所在的楼层高度就应该刚好为k。这样一来如果第一次测试第一枚鸡蛋破碎,则剩下k-1层楼,一层一层的试,k-1次内一定能完成目标(因为刚好剩下k-1次机会嘛),这样就使得每一次的机会都最大化了其效用。
如果第一次测试,第一枚鸡蛋没有破碎,则我们现在只有k-1次测试机会了,但却测试出了k楼及其以下都是安全的。我们消耗了一次测试机会,但是一次就测试了k层楼。
然后只有k-1次机会了,第二次测试,我们可以在k层的基础上再增加k-1层了,注意,这个时候由于我们只有k-1次机会,所以这次只能再增加k-1层,以保证测试的时候第一枚鸡蛋破碎的情况下仍然能完成任务。
于是,重复上述过程,直到最后一次机会,那么我们总共测试的楼层数就为:
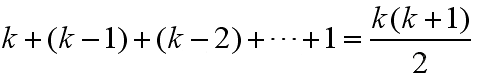
然后,再回到“原始问题”,100层楼,如果需要k次测试才能测试完成,则必须有:
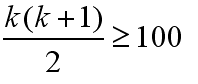
则可以得到,k≥14
也就是至少需要14次测试才能得到结果,而且这个过程也将测试方案一并得出来,就是第一次在14楼测试,如果第一枚蛋碎,则剩余13次机会,13层未知楼层,恰好。如果没碎,则第二次在14+13=27楼测试,如此循环。
如果不是100层,而是N层,需要的测试次数为k,则有

然后,这个问题此时就可以扩展了:如果我们有三个鸡蛋,有k次机会,我们最大可以测试多少层楼?
思路同前面一样,第一次测试,不能太高也能太矮,必须恰到好处,也就是第一枚鸡蛋如果破碎,剩余k-1次机会能将剩余楼层给测试完。
由上面结论,两个鸡蛋,k-1次机会最多可以测试k(k-1)/2层楼,所以第一次在k(k-1)/2+1层楼,第一次如果第一枚鸡蛋不碎,第二次在此基础上增加(k-1)(k-2)/2+1层楼,于是,三个鸡蛋k次机会总共测试楼层数为:

至于四个鸡蛋,五个鸡蛋,以至于M个鸡蛋,可以以此类推,方法同上。
再回到本题中来,3个鸡蛋,1000层楼
那么我们直接带上面已经推出来的公式,即:
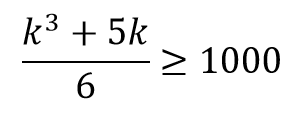
解之即可(可以验证,两种思路下得到的结果均一致,为19)
这篇关于【蓝桥杯】 第九届国赛 第四题 测试次数(动态规划)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



