透彻理解“对数”概念及其在量化交易中的意义

本文主要是介绍透彻理解“对数”概念及其在量化交易中的意义，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

透视一个数学概念，目前看需要从三个层面：数学史、数学概念、数学意义。

学校教育，不教数学史，不教其实际意义，只教概念，完全是混蛋无赖做法。

• 对数的发展史

对数之前是等差、等比数列。

1. 15世纪，法国数学家N.Chuquet(1445-1488)在其《算学三部》中给出双数列的对应关系。

1 2 4 8 16 32 64 128 ... # 数列一：等比数列
0 1 2 3 4  5  6   7 ...  # 数列二：等差数列

等比数列中的乘除关系，对应等差数列中的加减关系

例如 2 * 8 = 16 对应 1 + 3 = 4

2. 16世纪，德国数学家M.stifel(1487-1567)明确提出等比数列的乘、除、乘方、开方四种运算法则，但当时没有指数概念，并未产生实际物理推动意义
3. 1614年，苏格兰数学家J.Napier(1550-1617)出版《奇妙的对数定理说明书》，对数概念正式诞生
4. 随后，伦敦数学家H.Briggs(1561-1630)建议改进Napier的对数，使1的对数为0,10的对数为1。出版更简便的常用对数表。
5. 17世纪，R.Descartes(1596-1650)发明幂的记号，指数概念顺势诞生。
6. 17世纪末，对数可以定义为幂指数，被发现。
7. 随后，L.Euler(1707-1783)深刻揭示了指数与对数之间的密切联系，并创用了$Lo{g}_{a}N$这一记号。

• 对数的概念

古巴比伦复利问题，年息20%，几年后本金能变成2。

$1.2^x=2$，$x=?$

J.Napier之前，世人没有办法表示x的结果，J.Napier将其称为’logarithm’(这个词源自希腊文logos（比）和arithmos（数）组合而成．后来，数学家又把它简化成符号“log”).

因此，x便有了新的表示方法：

$x=lo{g}_{1.2}2$

推广到一般情况，就有了对数的定义：

若$a^b=N$（a > 0, a != 1），则数$b$叫做以$a$为底$N$ 的对数，记作
$$b={\log }_{a}N$$
其中$a$为底数，$N$为真数，读做以$a$为底$N$的对数

• 对数的意义

对数的发明是计算的革命，法国数学家与天文学家P.S.Laplace(1749-1827)：“对数倍增了天文学家的寿命，因为省时省力”。

数学家们感慨：“没有什么比大数的乘、除、开平方或开立方运算更让数学工作者头痛、更阻碍计算者的了．这不仅浪费时间，而且容易出错”。

没有计算器的时代，天文学家要计算一个空间距离，需要耗费巨大的时间，因为都是大数（光速：299792.468Km/s，一年秒数31,536,000 s）。

对数的出现，让大数的乘、除工作转变为小数据的加、减工作，极大降低计算能耗。

• 对数坐标系

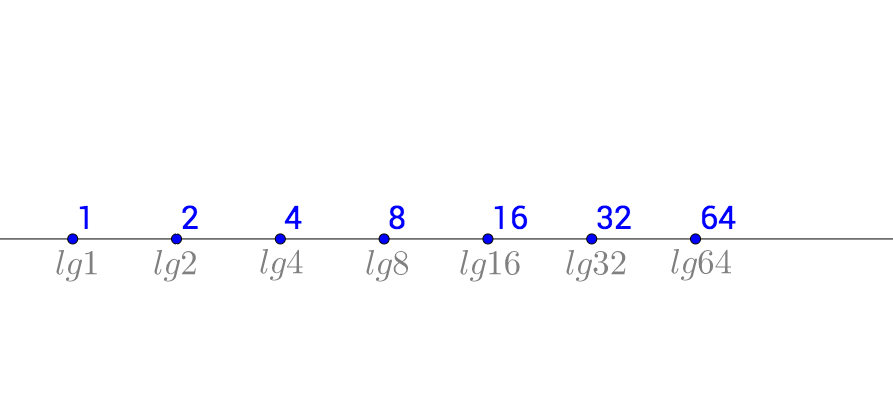
对数坐标系是将数轴进行强力缩放，一亿左右经对数缩放后也不过是8，这样在常规坐标系下巨大数据就可以在对数坐标系中简单表示，最典型的的应用就是天文学中绘图，如果按常规比例，怎么画太阳到地图、水星、金星等行星到一张图中？有了对数坐标系就很简单。

将大数实现小额化、归一化。这就是对数坐标系的价值。也是对数，最重要的意义。

• 参考

1. 钟萍,汪晓勤. 对数概念:从历史到课堂[J]. 中学数学月刊,2015(5):50-53.
2. 知乎-如何理解对数

.
.
.
2019-03-18 16:34:32写于上海

这篇关于透彻理解“对数”概念及其在量化交易中的意义的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---