本文主要是介绍【优选算法】双指针 -- 快乐数 和 盛最多水的容器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
前言：
🎯个人博客：Dream_Chaser
🎈刷题专栏：优选算法篇
📚本篇内容：03快乐数 和 04盛最多水的容器
目录
一、快乐数（medium）
1. 题⽬链接：202. 快乐数
2. 题⽬描述：
3. 题⽬分析:
4.算法原理
二、盛最多水的容器
1. 题⽬链接：11.盛最多水的容器 - 力扣（LeetCode）
2. 题⽬描述：
3. 解法⼀（暴⼒求解）（会超时）：
4. 解法⼆（对撞指针）：
一、快乐数（medium）
1. 题⽬链接：202. 快乐数
2. 题⽬描述：
编写⼀个算法来判断⼀个数 n 是不是快乐数。
「快乐数」 定义为：
◦ 对于⼀个正整数，每⼀次将该数替换为它每个位置上的数字的平⽅和。
◦ 然后重复这个过程直到这个数变为 1，也可能是⽆限循环但始终变不到 1 。
◦ 如果这个过程 结果为 1 ，那么这个数就是快乐数。
◦ 如果 n 是 快乐数 就返回 true ；不是，则返回 false 。
⽰例 1：
输⼊： n = 19
输出： true
解释：
19 -> 1 * 1 + 9 * 9 = 82
82 -> 8 * 8 + 2 * 2 = 68
68 -> 6 * 6 + 8 * 8 = 100
100 -> 1 * 1 + 0 * 0 + 0 * 0 = 1
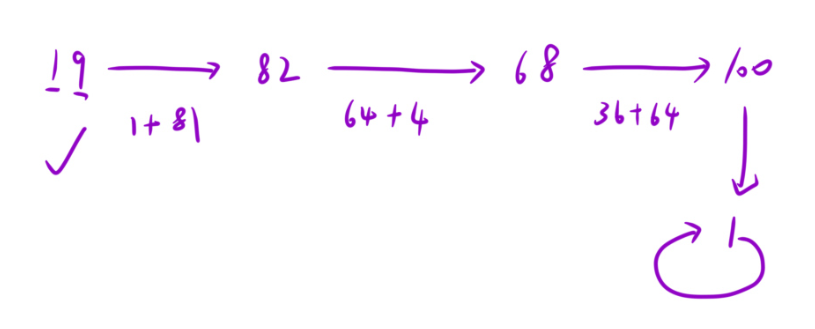
⽰例 2：
输⼊： n = 2
输出： false
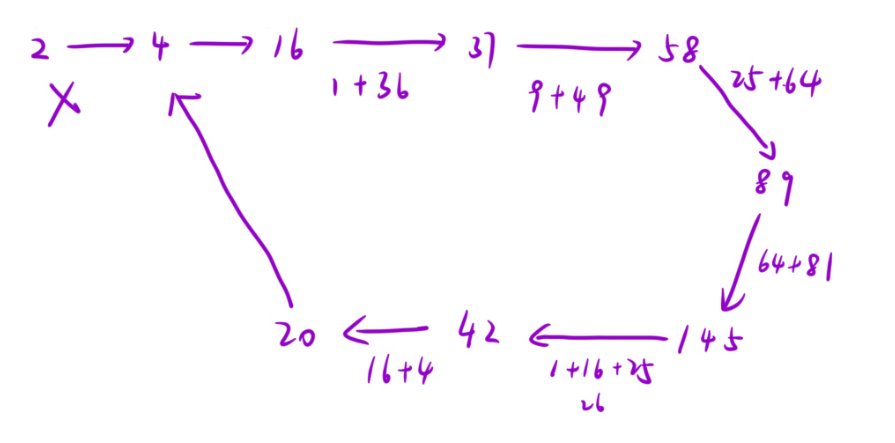
2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4 -> 16
3. 题⽬分析:
为了⽅便叙述，将「对于⼀个正整数，每⼀次将该数替换为它每个位置上的数字的平⽅和」这⼀个操作记为 f 操作；
题⽬告诉我们，当我们不断重复 f 操作的时候，计算⼀定会「死循环」，死的⽅式有两种：
▪ 情况⼀：⼀直在 1 中死循环，即 1 -> 1 -> 1 -> 1......
▪ 情况⼆：在历史的数据中死循环，但始终变不到 1
由于上述两种情况只会出现⼀种，因此，只要我们能确定循环是在「情况⼀」中进⾏，还是在「情况⼆」中进⾏，就能得到结果。
那么有没有可能有第三种情况，这个数在不段变化之中，不能达到死循环，但是以一种不断变化的方式呈现下去呢？
为了证明上述情况不存在，这里就需要说一下鸽巢原理：
简单证明：
a.经过⼀次变化之后的最⼤值 9^2 * 10 = 810 ( 2^31-1=2147483647 。选⼀个更⼤的最⼤ 9999999999 )，也就是变化的区间在 [1, 810] 之间；
b. 根据「鸽巢原理」，⼀个数变化 811 次之后，必然会形成⼀个循环；
c. 因此，变化的过程最终会⾛到⼀个圈⾥⾯，因此可以⽤「快慢指针」来解决。
4.算法原理
根据上述的题⽬分析，我们可以知道，当重复执⾏ x 的时候，数据会陷⼊到⼀个「循环」之中。 ⽽「快慢指针」有⼀个特性，就是在⼀个圆圈中，快指针总是会追上慢指针的，也就是说他们总会相遇在⼀个位置上。如果相遇位置的值是 1 ，那么这个数⼀定是快乐数；如果相遇位置不是 1 的话，那么就不是快乐数
补充知识：如何求⼀个数 n 每个位置上的数字的平⽅和。
a. 把数 n 每⼀位的数提取出来：
循环迭代下⾯步骤：
i. int t = n % 10 提取个位；
ii. n /= 10 ⼲掉个位；
直到 n 的值变为 0 ；
b. 提取每⼀位的时候，⽤⼀个变量 tmp 记录这⼀位的平⽅与之前提取位数的平⽅和
▪ tmp = tmp + t * t
代码实现：
class Solution {
public:int bitSum(int n){int sum = 0;//把数 n 每⼀位的数提取出来：while(n){ int t= n%10; // 提取个位//提取每⼀位的时候，//⽤⼀个变量 sum 记录这⼀位的平⽅与之前提取位数的平⽅和sum += t*t;n/=10; //n /= 10 ⼲掉个位；}return sum;}bool isHappy(int n) {int slow = n ,fast = bitSum(n);//快指针在下一个位置while(slow != fast){slow = bitSum(slow);//慢指针一次走一步fast = bitSum(bitSum(fast));//快指针一次走两步}return slow == 1;}
};
二、盛最多水的容器
1. 题⽬链接：11.盛最多水的容器 - 力扣（LeetCode）
2. 题⽬描述：
给定⼀个⻓度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的⽔。 返回容器可以储存的最⼤⽔量。
说明：你不能倾斜容器。
⽰例 1：
输⼊： [1,8,6,2,5,4,8,3,7]
输出： 49
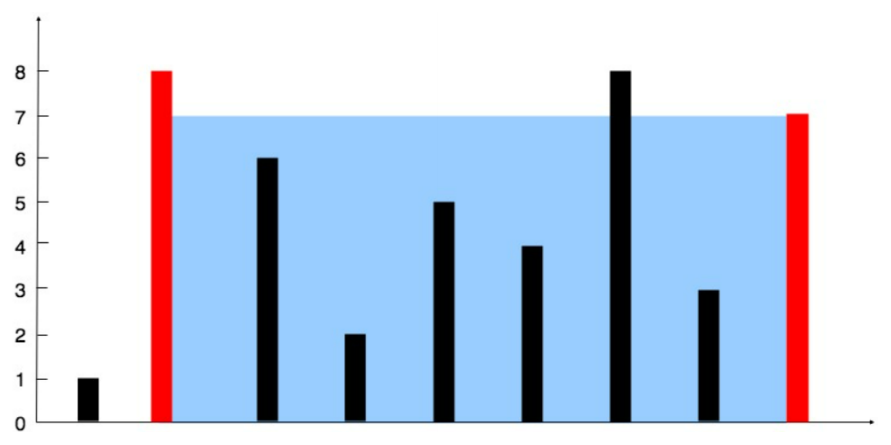解释：图中垂直线代表输⼊数组 [1,8,6,2,5,4,8,3,7] 。在此情况下，容器能够容纳⽔（表⽰为蓝⾊部分）的最⼤值为 49
3. 解法⼀（暴⼒求解）（会超时）：
算法思路：
枚举出能构成的所有容器，找出其中容积最⼤的值。
◦ 容器容积的计算⽅式：
设两指针 i , j ，分别指向⽔槽板的最左端以及最右端，此时容器的宽度为 j - i 。由于容器的⾼度由两板中的短板决定，因此可得容积公式 ： v = (j - i) * min(height[i], height[j])
算法代码：
class Solution {
public:
int maxArea(vector<int>& height)
{int n = height.size();int ret = 0;// 两层 for 枚举出所有可能出现的情况for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++){// 计算容积，找出最⼤的那⼀个ret = max(ret, min(height[i], height[j]) * (j - i));}}return ret;
}
};4. 解法⼆（对撞指针）：
算法思路：
设两个指针 left ， right 分别指向容器的左右两个端点，此时容器的容积 :
v = (right - left) * min( height[right], height[left])
容器的左边界为 height[left] ，右边界为 height[right] 。
为了⽅便叙述，我们假设「左边边界」⼩于「右边边界」。
如果此时我们固定⼀个边界，改变另⼀个边界，⽔的容积会有如下变化形式：
◦ 容器的宽度⼀定变⼩。
◦ 由于左边界较⼩，决定了⽔的⾼度。如果改变左边界，新的⽔⾯⾼度不确定，但是⼀定不会超过右边的柱⼦⾼度，因此容器的容积可能会增⼤。
◦ 如果改变右边界，⽆论右边界移动到哪⾥，新的⽔⾯的⾼度⼀定不会超过左边界，也就是不会超过现在的⽔⾯⾼度，但是由于容器的宽度减⼩，因此容器的容积⼀定会变⼩的。
由此可⻅，左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界，继续去判断下⼀个左右边界。
当我们不断重复上述过程，每次都可以舍去⼤量不必要的枚举过程，直到 left 与 right 相遇。期间产⽣的所有的容积⾥⾯的最⼤值，就是最终答案。
首先我们看看这个数组：
从数组中取出一部分分析：
其实最重要的一点我们需要理清楚的是，我们要求的是在这么多体积之中求最大值，所以在两指针遍历过程中把高度较小那个干掉就行：
类似这样。
代码实现：
class Solution {
public:int maxArea(vector<int>& height) {int left = 0,right =height.size()-1,ret=0;while(left<right){int v = min(height[left],height[right])*(right-left);ret = max(ret,v);if(height[left]<height[right]){left++;}else{right--;}}return ret;}
};
本篇完。
🔧本文修改次数：0
🧭更新时间：2024年3月26日
这篇关于【优选算法】双指针 -- 快乐数 和 盛最多水的容器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
