距离首都距离

本文主要是介绍距离首都距离，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

路径数组转化为统计数组

距离首都距离

给定一个路径数组paths，表示一张图。
paths[i]==j代表城市i连向城市j，
  如果 paths[i]==i，则表示i城市是首都;
  一张图里只会有一个首都且图中除首都指向自己之外不会有环。

nums[i]==j代表距离首都为i的城市有j座。
要求实现一个void类型的函数，输入一个路径数组paths，直接在原数组上调整，使之变为nums数组。
若paths长度为N，请达到时间复杂度为O（N），额外空间复杂度为O（1）。

举例：
paths = [9, 1, 4, 9, 0, 4, 8, 9, 0, 1]
如下图所示。

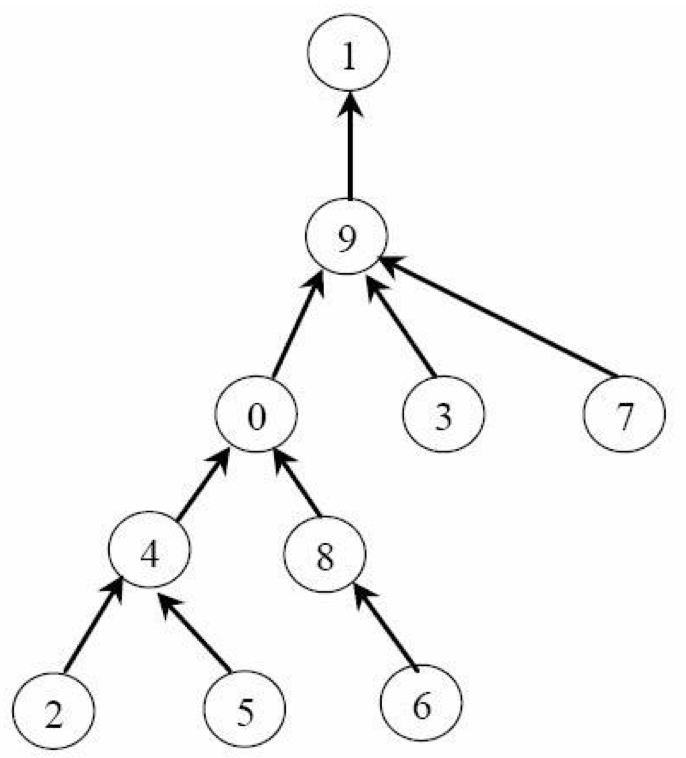
根据题意，首都为1，以首都为原点，计算每个城市与之的距离。
  0距离1为2，1距离1为0，2距离1为4，3距离1为2，4距离1为3，5距离1为4，
  6距离1为4，7距离1为2，8距离1为3，9距离1为1。
因此统计距离首都的城市数量的统计数组为：
  nums = [1, 1, 3, 2, 3, 0, 0, 0, 0, 0]

算法思路

第一步是将路径数组转换为距离数组：[9, 1, 4, 9, 0, 4, 8, 9, 0, 1] -> [-2, 0, -4, -2, -3, -4, -4, -2, -3, -1]
第二步是将距离数组转换为统计数组：[-2, 0, -4, -2, -3, -4, -4, -2, -3, -1] -> [1, 1, 3, 2, 3, 0, 0, 0, 0, 0]

注意：
生成距离数组的时候，值设置为负数，可以标记状态，更便于转换成统计数组。
路径转成距离数组的过程中，每一个城市只经历跳出去和跳回来两个过程，距离数组转成统计数组的过程也是如此，所以时间复杂度为$O（N）$，
整个过程没有使用额外的数据结构，只使用了有限几个变量，所以额外空间复杂度为$O（1）$。

相应代码

# 路径数组转换为距离数组
# 距离以负数表示
def pathsToDistances(paths):for i in range(0, len(paths)):if paths[i] == i:cap = ielif paths[i] >= 0:index = paths[i]paths[i] = -1pre_index = i# 向前跳while paths[index] >= 0 and paths[index] != index:next_index = paths[index]paths[index] = pre_indexpre_index = indexindex = next_indexif paths[index] == index:dis = 0else:dis = paths[index]# 往回跳index = pre_indexwhile paths[index] != -1:pre_index = paths[index]dis = dis - 1paths[index] = disindex = pre_indexdis = dis - 1paths[index] = dispaths[index] = dis# 首都距离为0paths[cap] = 0# 距离数组转换为统计数组
def distancesToStatistic(paths):for i in range(len(paths)):# 负数为未统计值if paths[i] < 0:index = -paths[i]paths[i] = 0  # 可以设置值# index向前统计while paths[index] < 0:next_index = -paths[index]paths[index] = 1index = next_indexpaths[index] += 1paths[0] = 1def pathsToStatistic(paths):pathsToDistances(paths)distancesToStatistic(paths)# 简单测试
if __name__ == '__main__':paths = [9, 1, 4, 9, 0, 4, 8, 9, 0, 1]pathsToStatistic(paths)print(paths)

有任何疑问和建议，欢迎在评论区留言和指正！

感谢您所花费的时间与精力！

这篇关于距离首都距离的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---