统计学的描述统计

本文主要是介绍统计学的描述统计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

统计学的描述统计

1.0 描述统计

1.1 峰度、偏度

均值 < 中位数 ，左偏
中位数 < 均值 ，右偏

1.2 相关性分析

1.2.1 单变量分析

1.2.2 双变量分析

皮尔逊相关系数（person）
（强调的是可能性）

• 目的：
  计算两个数值型数据之间的线性关系，当两个变量之间的关系是非线性时，相关系数为0.

• 取值范围：
  [-1,1]，正数代表正相关，负数代表负相关。

• 相关系数分类：
  0.8 - 1.0（极强相关）；
  0.6 - 0.8（强相关）；
  0.4 - 0.6（中等程度相关）；
  0.2 - 0.4（弱相关）；
  0 - 0.2（极弱相关或无相关）

• 皮尔逊相关系数的约束：
  1、两个变量有线性关系；
  2、变量是数值型变量（数值）；
  3、异常值较少；
  4、样本数最好大于30；
  5、变量标准差不能为0

斯皮尔曼相关系数（Spearman）

• 目的：是根据等级资料研究两个变量间相关关系的方法。

• 缺点：若变量为线性时，精确的没有皮尔逊高，效率比皮尔逊低（排序）
  优点：可以处理非线性关系，对异常值不敏感，可用于定序型离散值变量

相关和因果

相关：是两个或多个变量之间互相影响程度，核心点互为相关，同时存在，没有先后顺序。

因果：前一个事件对后一个事件的作用与强度，核心点是有先后顺序的。

举个例子——怎么判断相关和因果：
例子：定期接受体检就能长寿吗？，这是相关还是因果？
我们可以用5步方式来尝试判断

• 第一步，将要素套入到“原因”与“结果”中，依据经验看是否合理；比如这里，因为我们去体检了，所以我们长寿了。
• 第二步，查看此事是否纯属巧合？如果是，那就不能判为因果
• 第三步，是否存在同时影响原因和结果的第三变量？
• 第四步，否存在逆向因果关系。
• 第五步、制造反事实——如果不定期体检，健康会不会变差？寿命会不会明显变短？如果否，那就不能判为因果

1.3 异常检测

1.3.1 Ksigma法

1.3.2 切比雪夫定理：（5sigma法）

在任意一个数据集中
所有数据中，至少有3/4（或75%）的数据位于平均数2个标准差范围内。

所有数据中，至少有8/9（或88.9%）的数据位于平均数3个标准差范围内。

所有数据中，至少有24/25（或96%)的数据位于平均数5个标准差范围内

1.3.3 经验法则：(3sigma法）

当该数据集符合正态分布
那么有68.3%的数据位于平均数1个标准差范围内。

那么有95.5%的数据位于平均数2个标准差范围内。

那么有99.7%的数据位于平均数3个标准差范围内。

存在的缺点：

1. 需要数据服从正态分布或近正态分布。
   2.输出的正常区间容易受异常值影响而导致不准确。

1.3.4 Numeric Outlier（箱线图法）

1、计算第一四分位数（Q1）及第三四分位数（Q3）
2、计算IQR （IQR = Q3 - Q1）
3、输出正常区间[Q1-1.5IQR，Q3+1.5IQR]

比起3sigma，Numeric Outlier无需符合正态分布也能使用，并且能够避免异常值的影响，输出结果更精确。

2.0 概率

条件概率、贝叶斯、全概率公式

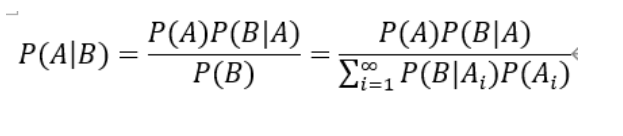
3.0 总结

这篇关于统计学的描述统计的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---