308. 区域和检索 - 数组可修改——从具体案例中讲解线段树的构造、更新

本文主要是介绍308. 区域和检索 - 数组可修改——从具体案例中讲解线段树的构造、更新，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

给你一个数组 nums ，请你完成两类查询。

1. 其中一类查询要求 更新 数组 nums 下标对应的值
2. 另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 用整数数组 nums 初始化对象
• void update(int index, int val) 将 nums[index] 的值 更新 为 val
• int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], ..., nums[right]）

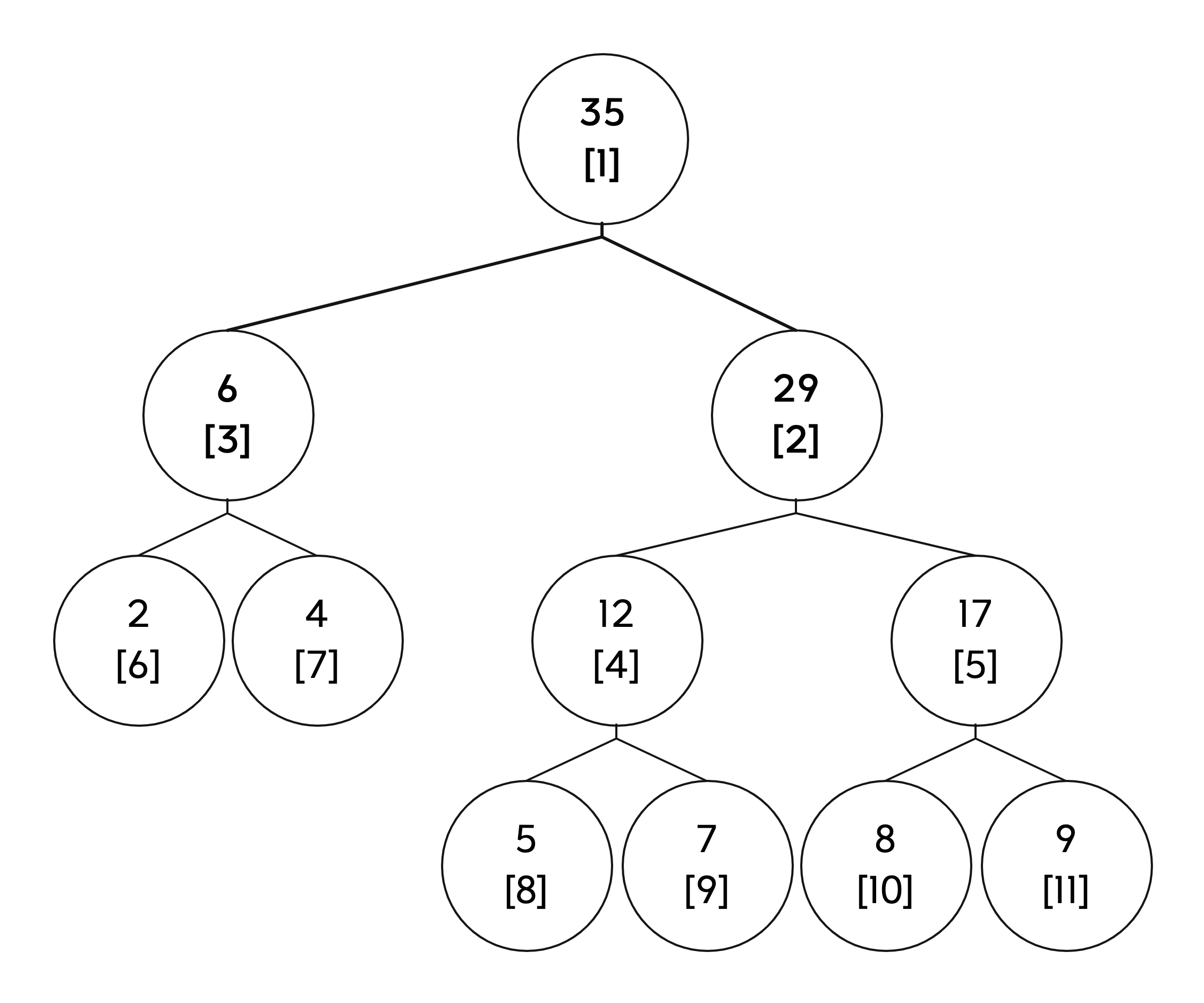
首先是线段树的构建如图所示：

步骤1：将原数组中的元素排列到新数组的后半部分

        for(int i = size, j = 0; i < 2 * size; ++i, ++j){tree[i] = nums[j];}

步骤2：两两计算父节点的值，由序号 / 2决定是否父节点相同
例如：6 / 2 == 7 / 2，所以元素2和元素4属于同一个父节点（新增的元素6）
下方虽然有三个图，但其实都属于同一个循环中的代码

        for(int i = size - 1; i > 0; --i){  //tree[0]不使用tree[i] = tree[i * 2] + tree[i * 2 + 1];}

接下来是线段树的更新：

同样采用从最底层进行更新，例如我们把样例中的元素8改为元素10

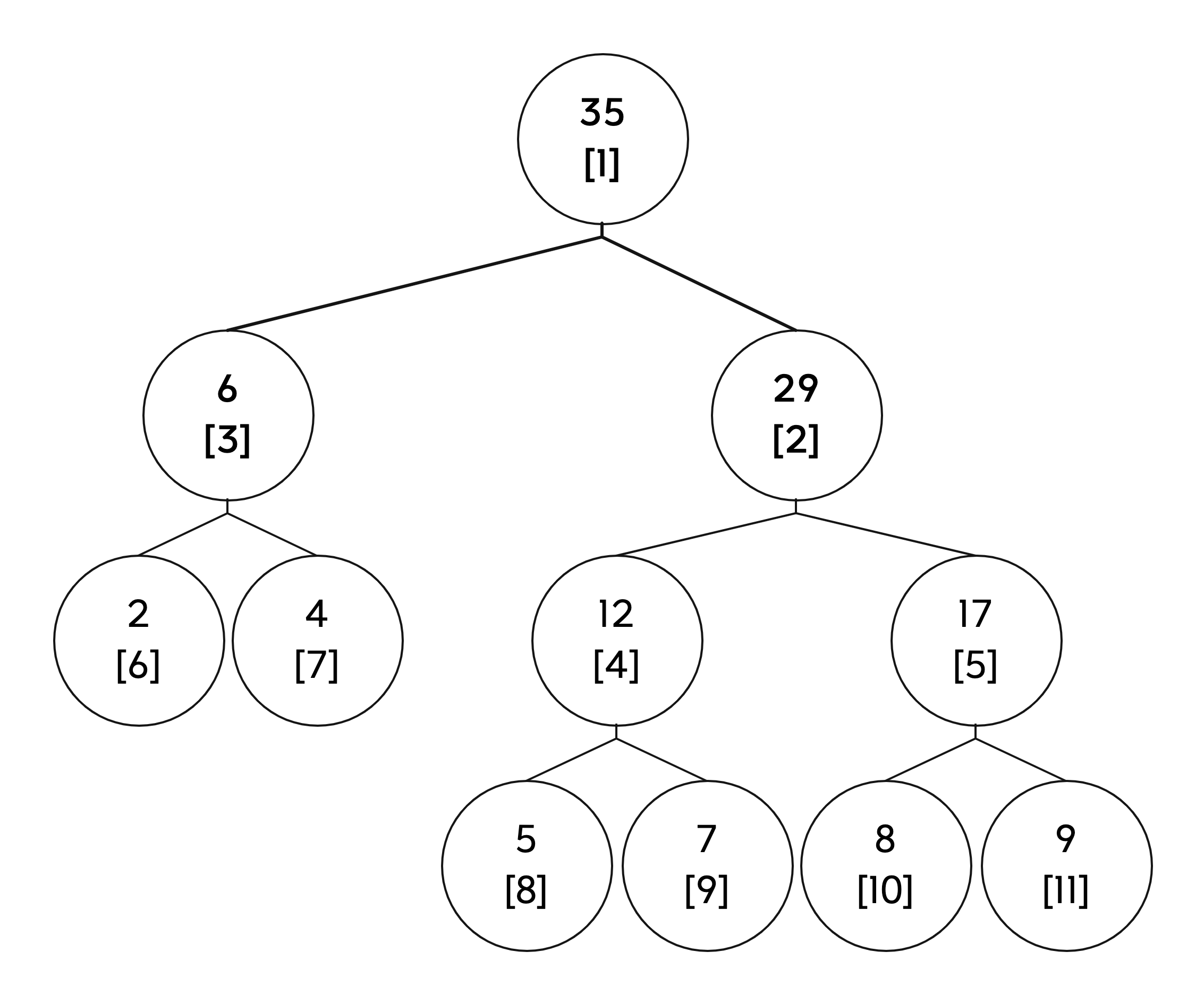
如图所示，对元素8及其父节点的值都进行了更新。
但是我们会面临2个问题：

1. 如何对元素8进行更新

   元素8其实很容易更新，因为样例中会告诉我们8在原数组中所在的位置index以及我们可以计算出原数组长度size，本样例中，8的序号为10 = index(4,从零开始) + size(6)。

2. 如何对父节点进行更新

   线段树很容易看出是一个类完全二叉树，即子节点与父节点之间存在倍数关系(n,2n,2n+1)。

   那么我们只需要对序号不断的除以2，可能遍历所有父节点，采用右移更加快速。

   此处其实还有一个小分叉口，我看到许多方法是tree[n] = tree[n * 2] + tree[n * 2 + 1]才更新父节点的值，但我觉得算出更新元素的差值，然后让父节点们与差值进行相加更快一点。

    void update(int index, int val) {int n = index + size;int diff = val - tree[n];tree[n] = val;//不断更新父节点while(n >> 1 > 0){n >>= 1;tree[n] += diff;}}

最后是算出范围内的元素总和

我们已经构建好线段树了，那么只需要找到各个所在子树中最高的节点进行相加即可。

例如在图示中求[1,4]的和，即4+5+7+8。我们找到各个所在子树中最高的节点，在此处是4+12+8。

即同时包含左右孩子节点的时候，去找他们父节点。

那么算法是怎么进行的呢？

我们可以发现，只有最左端和最右端可能存在他们的父节点只有一个孩子的情况。

            //如果左序号%2 == 1说明只包含该部分子树的右节点//那么就不能通过父节点来计算和，只能直接加该节点的和if(left % 2 == 1){sum += tree[left];left++; //上面已经将该部分子树唯一的节点已经加上了，直接右移看右半边的子树}//如果右序号%2 == 0说明只包含该部分子树的左节点//同理只能直接加该节点的和if(right % 2 == 0){sum += tree[right];right--;    //同理直接看左半边子树}

先将单节点的值加入总和，然后左节点向右移动、右节点向左移动（分情况而定）

这样可以在不疏忽单节点的情况下保证接下来在[left, right]之间是两两配对的

            left >>= 1;right >>= 1;

然后进入他们的父节点重复上述操作，最后就能得到各个所在子树中最高的节点的和了

最后附上全部的代码：

class NumArray {
public:vector<int> tree;int size;   //nums有n个元素，那么树的节点应该有2n - 1个//线段树的构造//线段树是完全二叉树NumArray(vector<int>& nums) {size = nums.size();tree.resize(2 * size);//先处理最后一层for(int i = size, j = 0; i < 2 * size; ++i, ++j){tree[i] = nums[j];}//然后慢慢更新父节点//可以参考完全二叉树的构建中父节点与子节点的关系，第222题for(int i = size - 1; i > 0; --i){  //tree[0]不使用tree[i] = tree[i * 2] + tree[i * 2 + 1];}}//更新值void update(int index, int val) {int n = index + size;int diff = val - tree[n];tree[n] = val;//不断更新父节点while(n >> 1 > 0){n >>= 1;tree[n] += diff;}}//返回总和int sumRange(int left, int right) {int sum = 0;left += size;right += size;while(left <= right){//如果左序号%2 == 1说明只包含该部分子树的右节点//那么就不能通过父节点来计算和，只能直接加该节点的和if(left % 2 == 1){sum += tree[left];left++; //上面已经将该部分子树唯一的节点已经加上了，直接右移看右半边的子树}//如果右序号%2 == 0说明只包含该部分子树的左节点//同理只能直接加该节点的和if(right % 2 == 0){sum += tree[right];right--;    //同理直接看左半边子树}left >>= 1;right >>= 1;}return sum;}
};

这篇关于308. 区域和检索 - 数组可修改——从具体案例中讲解线段树的构造、更新的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---