本文主要是介绍代码随想录算法训练营第36天|738.单调递增的数字|968.监控二叉树|总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
代码随想录算法训练营第36天|738.单调递增的数字|968.监控二叉树|总结
738.单调递增的数字
https://programmercarl.com/0738.%E5%8D%95%E8%B0%83%E9%80%92%E5%A2%9E%E7%9A%84%E6%95%B0%E5%AD%97.html
class Solution {
public:int monotoneIncreasingDigits(int n) {string strnum=to_string(n);// flag用来标记赋值9从哪里开始// 设置为这个默认值,为了防止第二个for循环在flag没有被赋值的情况下执行int flag=strnum.size();for(int i=strnum.size()-1;i>0;i--){if(strnum[i]<strnum[i-1]){flag=i;strnum[i-1]--;}}for(int i=flag;i<strnum.size();i++){strnum[i]='9';}return stoi(strnum);}
};
总结
就是从后往前遍历,然后依次把前大值降数,然后把cur数计flag以来放9。
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
确定了遍历顺序之后,那么此时局部最优就可以推出全局,找不出反例,试试贪心。
其中的flag初值需要注意应该是strnum.size()。
968.监控二叉树 (可以跳过)
本题是贪心和二叉树的一个结合,比较难,一刷大家就跳过吧。
https://programmercarl.com/0968.%E7%9B%91%E6%8E%A7%E4%BA%8C%E5%8F%89%E6%A0%91.html
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int result=0;int traversal(TreeNode* node){if(node==NULL) return 2;int left=traversal(node->left);// 左int right=traversal(node->right);// 右if(left==2 &&right==2) return 0;else if(left==0||right==0) {result++;return 1;}else return 2;}int minCameraCover(TreeNode* root) {// root 无覆盖if(traversal(root)==0) result++;return result;}
};
总结
通过二叉树的性质来运用贪心算法,把结点4个情况处理完成,然后遍历全部整个树最后,以局部最优来达成全局最优。
有如下三种:
该节点无覆盖
本节点有摄像头
本节点有覆盖
我们分别有三个数字来表示:
0:该节点无覆盖
1:本节点有摄像头
2:本节点有覆盖
情况1:左右节点都有覆盖
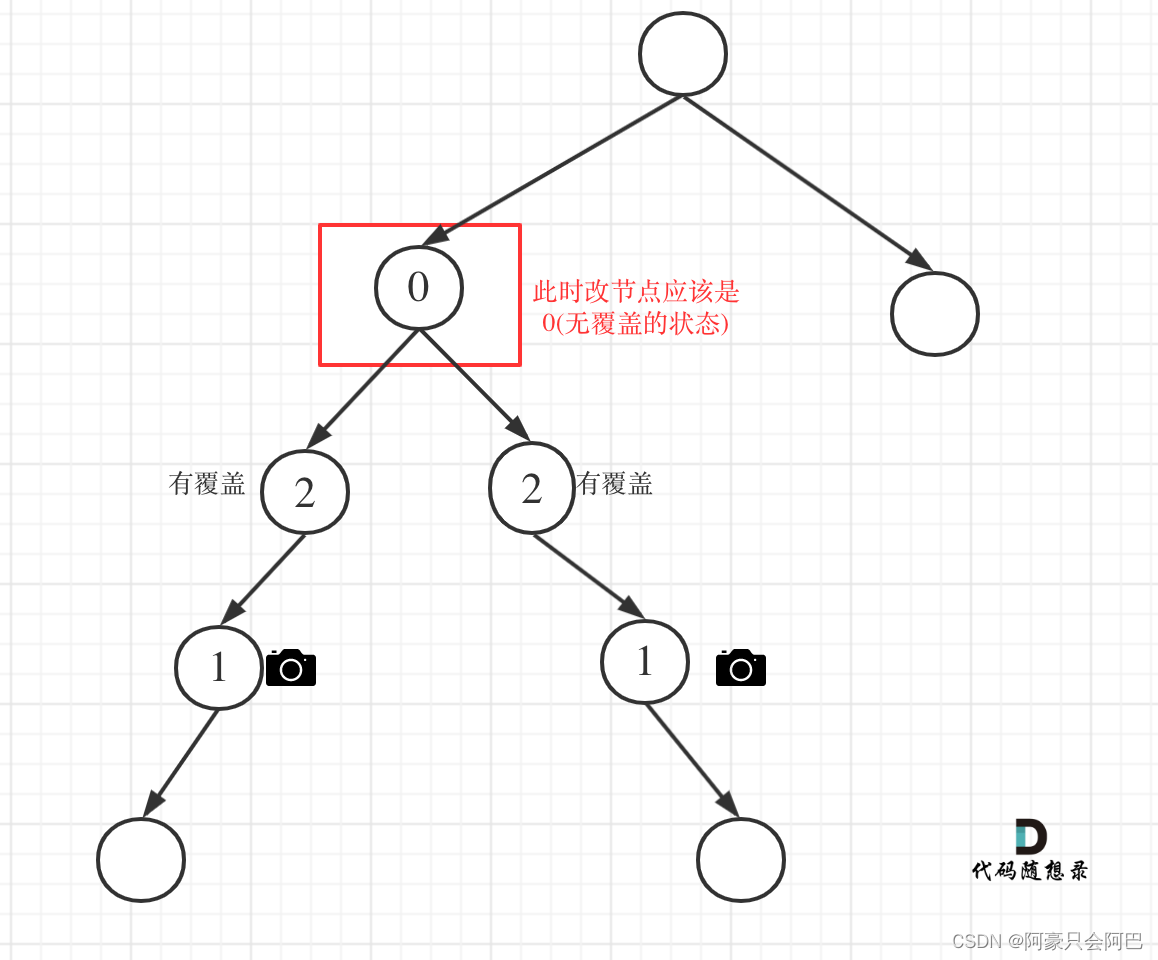
情况2:左右节点至少有一个无覆盖的情况
left == 0 && right == 0 左右节点无覆盖
left == 1 && right == 0 左节点有摄像头,右节点无覆盖
left == 0 && right == 1 左节点有无覆盖,右节点摄像头
left == 0 && right == 2 左节点无覆盖,右节点覆盖
left == 2 && right == 0 左节点覆盖,右节点无覆盖
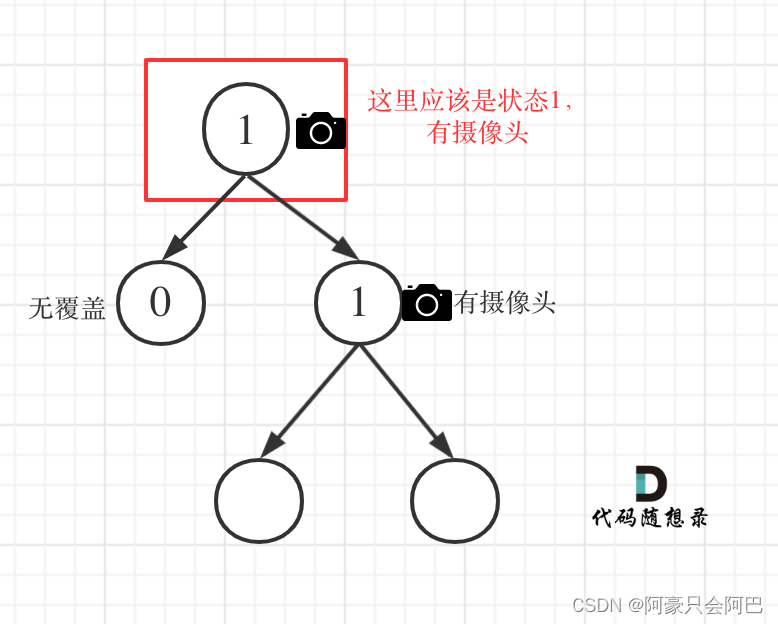
情况3:左右节点至少有一个有摄像头
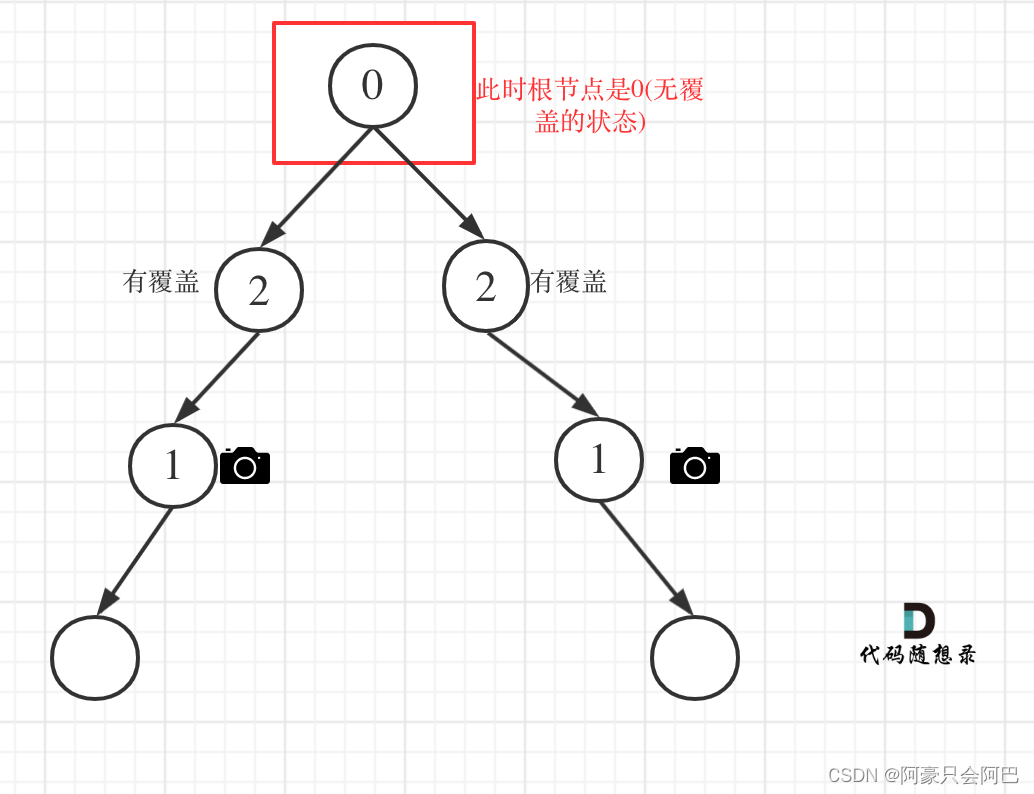
情况4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图:
总结
可以看看贪心算法的总结,贪心本来就没啥规律,能写出个总结篇真的不容易了。
https://programmercarl.com/%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95%E6%80%BB%E7%BB%93%E7%AF%87.html
这篇关于代码随想录算法训练营第36天|738.单调递增的数字|968.监控二叉树|总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






