本文主要是介绍卷积网络调参，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1、调参技巧
1.1、优化算法
在神经网络训练中，我们希望每次训练使损失值更小，即通过优化算法调整参数使得模型向损失更小的方向发展。
梯度下降算法：通过求偏导找到函数值减小的方向，从而使参数朝该方向移动
其中Θ为需要调整的参数，L(x,y)为函数值，通过dL/dΘ求出使L减小的方向（即梯度），再与学习率α相乘，得到参数调整的值，再用当前的Θ减去该值，得到新的参数Θ。类似于一个下山的过程，Θ为当前位置，dL/dΘ为找到下山最快的方向，α为朝该方向移动的距离，由当前位置朝下山方向移动一个距离便得到新的、离山下更近的位置。α如果太小，则“下山”速度太慢，无法尽快得到最值。如果α过大，则会越过最低点，无法到达最值点。
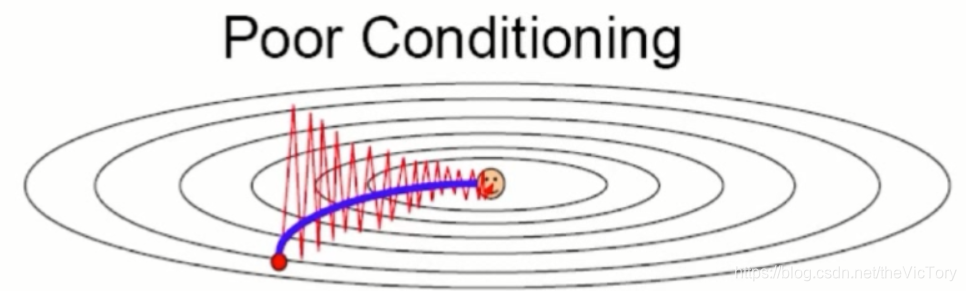
如果每次都在整个数据集上计算损失和梯度会带来庞大的计算量，当数据量过于庞大时机器无法承载。这是可以采用随机梯度下降法(Stochastic Gradient Descent,SGD)，每次只采用一个样本计算梯度。但这样的样本无法代表整体数据信息，这时使用Mini Batch梯度下降法，随机从整体中选取一部分数据作为样本。梯度下降是依赖于导数寻找优化方向的，当导数为0时，梯度下降便失去了作用。例如下图左边的局部最优解是由于函数的一阶导数为0造成的，右边的鞍点是由于二阶导数为0造成的。这两种情况由于导数为0，不会继续优化寻找最优解。
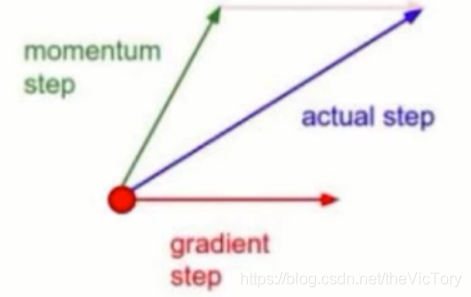
动量梯度下降法的前进方向是由之前的方向与当前方向的矢量相加而来的，由于存在之前累积的前进方向，当梯度的导数为0时，仍然会继续前进，跳过导数为0的陷阱寻找最优解。而且在避免梯度方向改变时，相反方向的矢量相加避免剧烈震荡，而在梯度方向一致时，同方向矢量相加，可以加速前进。
以上两种梯度下降算法的缺点是受到初始学习率的影响很大，而且无法个性化地为每一个维度指定不同的学习率。AdaGrade算法根据之前梯度的平方和得到一个积累值，以此作为学习率的分母，从而使学习率不断衰减，摆脱了对学习率初始值的依赖。在训练前期，积累值比较小，从而学习率很大，加速学习过程。而在训练后期，积累值变大，学习率随之减小，可以更好地去寻找最优解。把累计平方梯度变为平均平方梯度便得到了RMSProp算法，它解决了AdaGrade后期由于积累值过大学习率过小而提前结束学习的问题。
Adam算法结合了动量梯度下降算法和AdaGrade算法的优点，只需要设置好初始学习率，它会自动调整并寻找最优值。当需要训练较深较复杂的网络且需要快速收敛时可以使用。
1.2、激活函数
常见的激活函数如下图所示：
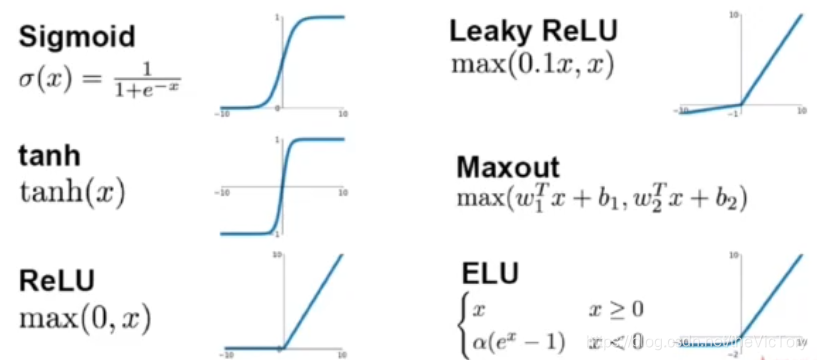
Sigmoid函数：从其图像上可以看出Sigmoid函数在输入绝对值增大时，输出变化趋于平缓，而且输出均值为正。从其表达式可以看出其计算较为复杂，对其求导可知，当神经网络变深时，会出现梯度消失。
梯度消失与爆炸：神经网络在反向传播时需要对每层参数求导，由链式求导法则，需要将每层的求导值相乘。比如求导值为0.1，当网络层数过多时，多个小数相乘会趋于0，这就是梯度消失。相反，如果导数值较大，多个相乘会导致梯度爆炸。
tanh函数在输入绝对值变大时输出梯度也会消失，其输出的均值为0，计算复杂
ReLU函数在输入小于0时输出0，大于0时输出原值。不会出现梯度消失，计算量小，收敛速度快，在其出现之后取代了Sigmoid称为使用最多的激活函数。其缺点是当神经元的输入存在负值时，输出0，没有导数，因此无法激活，神经元不会更新。为了解决这个问题，提出了Leaky ReLU函数，即在输入为负时不是输出0，而是乘以一个很小的系数后再输出。ELU函数是对小于0的输入坐指数处理，从而使输出的均值接近于0，从而其计算量变大。Maxout函数也是ReLU的泛化，对于输入的正和负，分别采用两套参数计算后输出。
1.3、网络初始化
一个初始化好的网络不仅训练得快，而且可以达到更好的效果。一个好的初始化值在经过激活函数后的值会分布在固定的区间内。如果都集中在某个值上，则初始化的值不好。
一个简单的初始化方法就是将所有参数都初始化为0，这仅适用于单层网络模型，多层网络会造成梯度消失，无法训练。
也可以使用正态分布作为初始化值，不同的的均值和方差对于不同的激活函数结果也不同。
为了使数据分布在固定的区间内，引入了批归一化（batch normalizing）操作，它可以将每一批的数据在每一层的输出控制在均值为0，方差为1的标准正态分布上。
1.4、其他技巧
在网络调参中，还有其他一些技巧：采用更多的训练数据和进行更多次的叠代，采用更多的GPU来加速训练。首先在简单的网络上实现训练，再逐步增加网络层次，提高准确率。
可以将网络先在一些标准数据集上进行测试，以保证网络模型是正确的， 也可以与其他标准数据集上的模型作对比。如果数据集过大，可以先在一小部分数据集上达到过拟合的效果，然后再跑大数据。可以使用现有的调整好的模型，在预训练好的网络模型上进行微调（Fine tuning）
1.5、代码调整
在代码中一般将卷积层封装为convert()函数，然后将使用的激活函数activation、初始化函数initializer作为参数传入，具体每层的卷积函数等于这两个参数。这样在调用convert()函数时，便可以只更改一个调用名，而修改所有卷积层的激活、初始化函数。
def convert(input,activation,initializer): # 将激活函数、初始化函数作为参数传入# 卷积层1_1conv1_1=tf.layers.conv2d(input,32,(3,3),padding='same',activation=activation, #激活函数kernel_initializer=initializer, # 初始化方法name='conv1_1' )# VggNet两个卷积层，一个池化层conv1_2=tf.layers.conv2d(conv1_1,32,(3,3),padding='same',activation=activation,kernel_initializer=initializer,name='conv1_2')# 池化层pool1=tf.layers.max_pooling2d(conv1_2, (2,2), (2,2), name='pool1')# 卷积层2_1、2_2与第二个池化层conv2_1=tf.layers.conv2d(pool1,32,(3,3),padding='same',activation=activation,kernel_initializer=initializer,name='conv2_1')conv2_2=tf.layers.conv2d(conv2_1,32,(3,3),padding='same',activation=activation,kernel_initializer=initializer,name='conv2_2')pool2=tf.layers.max_pooling2d(conv2_2,(2,2),(2,2),name='pool2') # 卷积层3_1、3_2与第三个池化层conv3_1=tf.layers.conv2d(pool2,32,(3,3),padding='same',activation=activation,kernel_initializer=initializer,name='conv3_1')conv3_2=tf.layers.conv2d(conv3_1,32,(3,3),padding='same',activation=activation,kernel_initializer=initializer,name='conv3_2')pool3=tf.layers.max_pooling2d(conv3_2,(2,2),(2,2),name='pool3')# 将卷积结果返回return pool3在调用convert()时传入具体的方法名
# 调用封装的卷积方法
res=convert(x_img,tf.nn.relu,tf.truncated_normal_initializer(stddev=0.02))还有其他的激活函数如tf.nn.sigmoid，其他的初始化方法tf.glorot_normal_initializer 、tf.keras.initializers.he_normal
优化方法的修改直接在定义优化方法时进行修改，例如采用AdamOptimizer：
#定义优化方法
with tf.name_scope('train_op'):train_op=tf.train.AdamOptimizer(1e-3).minimize(loss)# 之后在训练时传入train_op方法
loss_val,acc_val,_=sess.run([loss,accuracy,train_op],feed_dict={x:batch_data,y:batch_labels})还可以定义优化方法为梯度下降和动量优化法：
tf.train.GradientDescentOptimizer(1e-4).minimize(loss)
tf.train.MomentumOptimizer(learning_rate=1e-4,momentum=0.9).minimize(loss)2、参数可视化
可以借助于可视化工具来查看网络中间参数的状态，例如损失、梯度、准确率、学习率。
2.1、曲线分析
如下图为损失值的曲线图，其中黄色为测试集上的损失，蓝色为训练集上的
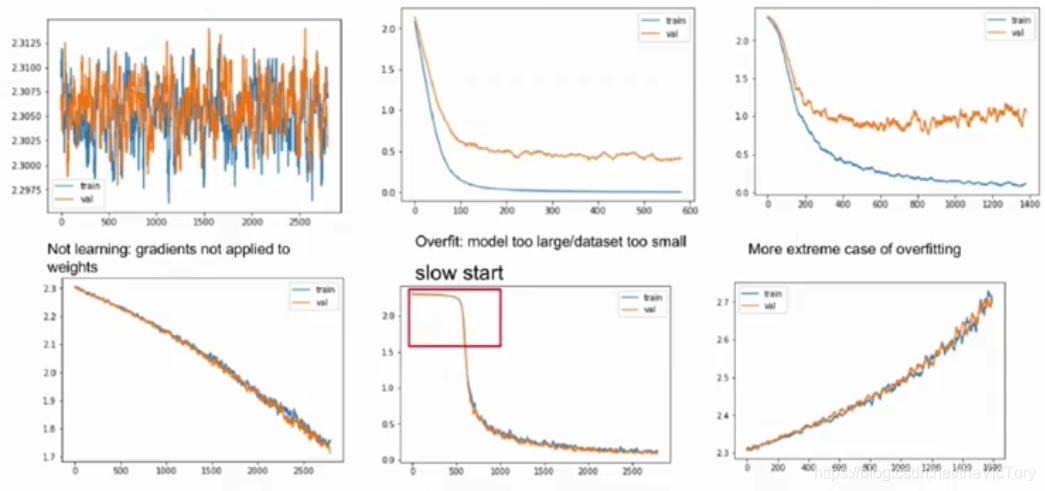
从第一幅图中可以看到损失值一直在震荡，说明模型没有拟合，可能由于学习率过大，导致模型反复越过最值点而无法达到该点。
第二幅图虽然在训练集上的损失已经降到很低且趋于稳定，但是在测试集上损失依然较大，这是由于模型出现了过拟合。第三幅图也是过拟合，训练集损失下降，测试集上的损失反而在上升。
第四幅图虽然训练集和测试集上的损失都在下降，但是与第二、第三幅相比可以看到其下降的趋势非常缓慢，这是由于学习率设置过小，导致拟合速度太慢，可以适当增大学习率。而且其损失曲线仍然具有下降的趋势，可以增加训练轮数，继续训练。
第五幅图可以看到在初始阶段曲线下降非常平缓，后来陡然增大，说明其初始化做得不太好。
第六幅图损失不降反增，可能是梯度方向弄错了
2.2、Tensor Board使用
使用步骤：
- 首先定义需要可视化的参数，最后将这些信息聚合
- 定义日志文件的保存路径
- 定义日志写入对象，并在训练过程中将日志信息写入文件
- 通过命令行运行Tensor Board：tensorboard --logdir=日志文件路径
之后就可以在浏览器内查看可视化结果，默认为localhost:6006
# TensorBoard可视化参数
# 1、首先定义需要显示的变量
loss_summary=tf.summary.scalar('loss',loss)
accuracy_summary=tf.summary.scalar('accuracy',accuracy)
# 将输入的图片作逆归一化处理，还原图像值
source_image=(x_img+1)*127.5
input_image=tf.summary.image('input_image',source_image)
# 将所有要显示的信息聚合
merged_train_summary=tf.summary.merge_all()
merged_test_summary=tf.summary.merge([loss_summary,accuracy_summary])# 2、指定日志保存路径
LOG_DIR='./TensorBoard_VGG_LOG'
if not os.path.exists(LOG_DIR):print('mkdir log')os.mkdir(LOG_DIR)
train_log_dir=os.path.join(LOG_DIR,'train')
test_log_dir=os.path.join(LOG_DIR,'test')
if not os.path.exists(train_log_dir):os.mkdir(train_log_dir)
if not os.path.exists(test_log_dir):os.mkdir(test_log_dir)init=tf.global_variables_initializer()
batch_size=20
train_steps=5000
test_steps=100with tf.Session() as sess:sess.run(init)# 3、定义日志写入对象，可以选择将模型图也写入train_writer=tf.summary.FileWriter(train_log_dir,sess.graph)test_writer=tf.summary.FileWriter(test_log_dir)# 保存一份固定的测试集数据fixed_test_data,fixed_test_labels=test_data.next_batch(batch_size)for i in range(train_steps):batch_data,batch_labels=train_data.next_batch(batch_size)loss_val,acc_val,_=sess.run([loss,accuracy,train_op],feed_dict={x:batch_data,y:batch_labels})# 每训练100次，执行summary操作并将结果写入日志文件if (i+1) % 100 ==0:train_summary_str=sess.run(merged_train_summary,feed_dict={x:batch_data,y:batch_labels})train_writer.add_summary(train_summary_str,i+1)test_summary_str=sess.run(merged_test_summary,feed_dict={x:fixed_test_data,y:fixed_test_labels})test_writer.add_summary(test_summary_str,i+1)if (i+1) % 500==0:print("第%d步：损失：%.5f，精确度：%.5f"%(i,loss_val,acc_val))#每训练1000次，在test数据集上进行一次测试if (i+1)%1000==0:# 定义测试集数据对象test_data=CifarData(test_file,False) all_acc=[]for j in range(test_steps):test_batch_data,test_batch_labels=test_data.next_batch(batch_size)test_acc=sess.run([accuracy],feed_dict={x:test_batch_data,y:test_batch_labels})all_acc.append(test_acc)# 将测得的多个准确率求均值test_acc_mean=np.mean(all_acc)print("第%d步测试集准确率%.4f"%(i,test_acc_mean))运行的结果如下图所示
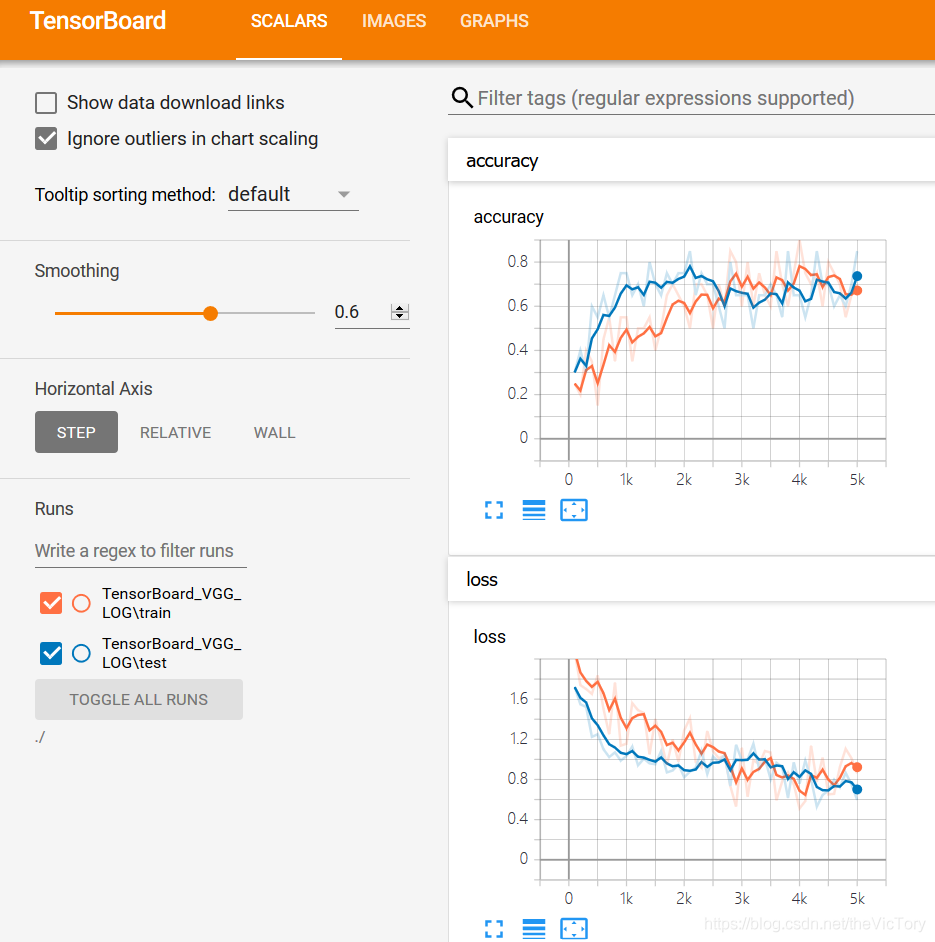
3、批归一化
随着神经网络训练层数的加深，每层网络的输出（在激活函数之前）分布逐渐往非线性函数取值区间的上下限两端靠近，从而导致反向传播时低层神经网络的梯度消失，造成神经网络收敛速度变慢。批归一化(Batch Normalization)就是将越来越偏的分布经过处理变为比较标准的分布，使得激活输入值落在非线性函数对输入比较敏感的区域，让梯度变大，避免梯度消失问题产生，加快学习收敛速度和训练速度。
- 归一化（Normalization）是把数据变为（0，1）之间的小数，主要是为了方便数据处理，因为将数据映射到0~1范围之内，可以使处理过程更加便捷、快速。最大最小归一化公式为：
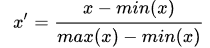，均值归一化：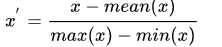
- 标准化（Standarlization）是为了方便数据的下一步处理，而进行的数据缩放等变换，并不是为了方便与其他数据一同处理或比较，比如数据经过0-1均值标准化后，更利于使用标准正态分布的性质进行处理；
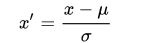其中 μ和 σ 分别是样本数据的均值（mean）和标准差（std） - 正则化（Regularization）是利用先验知识，在处理过程中引入正则化因子（regulator）,增加引导约束的作用，比如在逻辑回归中使用正则化，可以有效降低过拟合的现象。
把每个卷积操作封装为一个函数，在卷积时先不做激活操作，将卷积的结果通过tf.nn.batch_normalization()函数进行批归一化处理，之后再经过卷积函数将结果返回。
def convert_wrapper(x_input,name,train_flag,activation=tf.nn.relu,initializer=None):conv = tf.layers.conv2d(x_input, #输入32, #输出通道数(3,3), #卷积核大小padding='same', #填充使图小大小不变activation=None, #激活函数kernel_initializer=initializer, # 初始化方法name=name )bn = tf.layers.batch_normalization(conv,training=train_flag)# 将归一化的结果经激活函数后返回return activation(bn)def pooling_wrapper(x_input,name):return tf.layers.max_pooling2d(x_input, #输入(2,2), #池化核(2,2), #步长name=name)# 卷积层1_1
conv1_1=convert_wrapper(img_input, 'conv1_1',train_flag)
conv1_2=convert_wrapper(conv1_1,'conv1_2',train_flag)
conv1_3=convert_wrapper(conv1_2,'conv1_3',train_flag)
pool1=pooling_wrapper(conv1_3,'pool1')
# 卷积层2_1、2_2与第二个池化层
conv2_1=convert_wrapper(pool1,'conv2_1',train_flag)
conv2_2=convert_wrapper(conv2_1,'conv2_2',train_flag)
conv2_3=convert_wrapper(conv2_2,'conv2_3',train_flag)
pool2=pooling_wrapper(conv2_2,'pool2')
# 卷积层3_1、3_2与第三个池化层
conv3_1=convert_wrapper(pool2,'conv3_1',train_flag)
conv3_2=convert_wrapper(conv3_1,'conv3_2',train_flag)
conv3_3=convert_wrapper(conv3_2,'conv3_3',train_flag)
pool3=pooling_wrapper(conv3_2,'pool3')可以设置training参数控制是否进行批归一化，在训练数据集上进行归一化，在测试数据集上不需要，通过placeholder值train_flag来进行控制。
train_flag=tf.placeholder(tf.bool,[])
...
# 训练集
for i in range(train_steps):batch_data,batch_labels=train_data.next_batch(batch_size)loss_val,acc_val,_=sess.run([loss,accuracy,train_op],feed_dict={x:batch_data,y:batch_labels,train_flag:True})
# 测试集
test_acc=sess.run([accuracy],feed_dict={x:test_batch_data,y:test_batch_labels,train_flag:False})
这篇关于卷积网络调参的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
