1470 Closest Common Ancestors（简单的LCA算法）

本文主要是介绍1470 Closest Common Ancestors（简单的LCA算法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Description

Input

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times
For example, for the following tree:

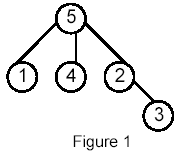
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)(2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Source

下面算法出处：http://blog.csdn.net/u012860428/article/details/38306327

• 该算法利用树中每个节点最多只有一个前驱。
• 寻找A,B的最近祖先，假设C为A的祖先，那么沿着A一定能到C。（B也同样如此）
• 
  因为是从下到上找的，所以最先找到的，就是最近的。

给出节点连接的子节点，根据此来建树，然后再给出一些数对，计算这两个节点的最近的公共节点并计数，最后全部查询完后，输出计数的个数；

[cpp] view plain copy

1. #include <iostream>  
2. #include <stdio.h>  
3. #include <string.h>  
4. #define MAX 1000  
5. using namespace std;  
6. int p[MAX];  
7. int cnt[MAX];  
8. void init(int n)  
9. {  
10.     int i;  
11.     for(i=0; i<=n; i++)  
12.         p[i]=i;  
13. }  
14. int query(int x,int y)  
15. {  
16.     int i,j;  
17.     if(p[x]==y)  
18.         return y;  
19.     if(p[y]==x)  
20.         return x;  
21.     for(i=x; p[i]!=i; i=p[i])//从当前节点开始，分别遍历x，y的父节点查找  
22.     {  
23.         for(j=y; p[j]!=j; j=p[j])  
24.         {  
25.             if(i==j)  
26.             {  
27.                 return j;  
28.             }  
29.         }  
30.     }  
31.     return i;  
32. }  
33. int main()  
34. {  
35.     int node,i,num,n,ccnode,x,y,ans,m;  
36.     //freopen("\\input.txt","r",stdin);  
37.    // freopen("\\output.txt","w",stdout);  
38.     while(~scanf("%d",&n))  
39.     {  
40.         memset(cnt,0,sizeof(cnt));//计数数组置零  
41.         init(n);  
42.         m=n;  
43.         while(n--)  
44.         {  
45.             scanf("\t%d\t:\t(\t%d\t)",&node,&num);  
46.   
47.             for(i=0; i<num; i++)  
48.             {  
49.                 scanf("\t%d\t",&ccnode);//输入节点  
50.                 p[ccnode]=node;//指定节点的父亲节点  
51.             }  
52.         }  
53.         scanf("%d",&n);  
54.         for(i=0; i<n; i++)  
55.         {  
56.             getchar();  
57.             scanf("\t(%d\t %d\t)",&x,&y);  
58.             ans=query(x,y);  
59.             cnt[ans]++;计数  
60.         }  
61.         //printf("%d:%d\n",14,cnt[14]);  
62.         for(i=0; i<=m; i++)//遍历输出  
63.         {  
64.             if(cnt[i]!=0)  
65.                 printf("%d:%d\n",i,cnt[i]);  
66.         }  
67.     }  
68.     return 0;  
69. } 
    

这篇关于1470 Closest Common Ancestors（简单的LCA算法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！