本文主要是介绍冈萨雷斯Matlab版第三章(亮度变换与空间滤波)知识点要点记录,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
术语“空间域”指的是图像平面本身,在空间域内处理图像的方法就是直接对图像的像素进行处理。
1、背景知识
本章中讨论的空间域处理由表达式
g(x, y) = T[f(x, y)]
表示,其中f(x, y)为输入图像,g(x, y)为输出(处理后的)图像,T是对图像f进行处理的操作符,定义在点(x, y)的指定邻域内。此外,T还可以对一组图像进行处理。
2、亮度变换函数
变换T的最简单形式就是领域大小为1*1时,此时(x, y)处的g值仅有f在该点处的亮度决定,T也变成了一个亮度或灰度级变换函数。当处理单色(灰度)图像时,这两个术语可以相互换用,当处理彩色图像时,亮度用来表示某个色彩空间中的一个彩色图像分量。
由于亮度变换函数仅取决于亮度值,所以亮度变换函数通常可以写作
s = T(r)
其中,r表示图像f中相应点(x, y)的亮度,s表示图像g中相应点(x, y)的亮度。
2.1、函数imadjust
函数imadjust是对灰度图像进行亮度变换的基本IPT工具
g = imadjust(f, [low_in high_in], [low_out high_out)], gamma
将图像f中的亮度值映像到g中,输入图像应为uint8类、uint16类或double类图像,输出图像与输入图像类相同。除图像f外,函数的输入指定在0~1之间,若是uint8类,将乘以255决定应用的实际值……, [low_in high_in]或[low_out high_out)]使用[] (空矩阵)得到默认值[0 1],若high_out < low_out输出亮度会翻转。
参数gamma指定了曲线的形状,该曲线用来映射f的亮度值
gamma < 1映射被加权至更高(更亮)的输出值
gamma > 1映射被加权至更低(更暗)的输出值
gamma = 1线性映射,默认值
2.2、对数变换和对比度拉伸变换
对数和对比度拉伸变换是进行动态范围处理的基本工具,对数变换的表达式为
g = c * log(1 + double(f))
其中,c是一个常数。
对数变换的一项主要应用是压缩动态范围,当执行一个对数变换时,我们通常期望将导致的压缩值还原为显示的全范围,对于8比特而言,使用语句
gs = im2uint8(mat2gray(g));
例
f = imread('1.png');
g = im2uint8(mat2gray(log(1 + double(f))));
imshow(g), figure, imshow(f);

下图表示对比度拉伸

阈值变换的函数形式为:
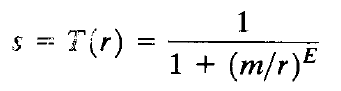
其中,r表示输入图像的亮度,s表示输出图像中的相应亮度值,E控制该函数的斜率,在MATLAB中的语句为:
g = 1 ./ (1 + (m ./ (double(f) + eps)) .^ E)
分母eps为了避免分母为0值时的溢出现象。上图的(a)表示E= 20。
2.3、亮度变换的一些实用M函数
处理可变数量的输入和/输出
检测输入到M函数的参量数目,我们可以使用函数nargin,该函数将返回输入到M函数的参量的实际数目,类似地,函数nargout用于M函数的输出,函数nargchk可用于一个M函数体中,以检测传递的参量数目是否正确,语法是
msg = nargchk(low, high, number)
该函数在number小于low时,返回消息Not enough input parameters,在number大于high时,返回消息Too many input parameters,若位于两者之间,返回空矩阵。
可变数目的输入变量用varargin,可变数目的输出变量用varargout。
亮度变换的自定义多功能函数
在这里,我们定义一个新的函数intrans,实现负片变换、对数变换、gamma变换和对比度拉伸变换。
changeclass函数将图像f转换为有参数newclass指定的类别,并输出图像g,newclass的有效值为'uint8', 'uint16', 'double',语法为:
g = changeclass(newclass, f)
changeclass函数m文件源码见:【MATLAB】图像处理相关函数intrans、changeclass函数
亮度标度的M函数——gscale
gsacle函数的语法为
g = gscale(f, method, low, high)
其中,f是将被标度的图像,method的有效值是'full8'(默认)和'full16',前者将输出标度为全范围[0, 255],后者将输出标度为全范围[0, 65 535],若使用这两个有效值之一,则可以在两种变换中省略参数low, high,method的第三个有效值为'minmax',此时我们给出low, high在范围[0, 1]内的值,然后程序本身会根据输入的类来执行适当的标度,然后将输出转换为与输入相同的类。
函数M文件源码见【MATLAB】图像处理相关函数gscale函数
3、直方图处理与函数绘图
本节重点在于获取、绘图并利用直方图技术进行图像增强
3.1 生成并绘制图像的直方图
一幅数字图像在范围[0, G]内总共有L个灰度级,其直方图定义为离散函数
h(rk) = nk
其中,rk是区间[0, G]内的第k级亮度,nk是灰度级为rk的图像中的像素数。对于uint8类图像, G的值为255 ,对于uint16类图像, G的值为 65535,对于double 类图像,G为 1.0。由于MATLAB中索引不为0,所以,r1相当于灰度级为0。
归一化直方图,即使用所有元素h(rk)除以图像中的像素总数n所得到的图形
p(rk) = h(rk) / n = nk / n
其中,k = 1, 2, ···, L,所以p(rk)表示灰度级rk出现的频数。
核心函数imhist的语法为 :
h = imhist(f, b)
其中,f为输入图像, h为其直方图h(rk),b是用于形成直方图的“收集箱”的个数(即灰度级个数),默认值256.
使用表达式
p = imhist(f, b) / numel (f)
可以得到归一化直方图。函数numel(f)给出数组f中的元素个数(即图像中的像素值)。
3.2 直方图均衡化
假设灰度级为归一化至范围[0, 1]内的连续量,并令pr(r)表示某给定图像中的灰度级的概率密度函数,假设我们对输入灰度级执行如下变换,得到输出灰度级s:
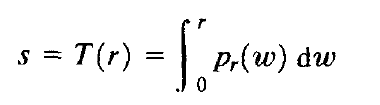
输出灰度级的概率密度函数是均匀的,即

灰度级均衡化处理的最终结果是一幅扩展了动态范围的图像,具有较高的对比度。
对于离散的灰度级,采用求和方式:
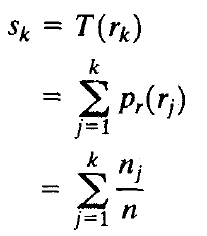
sk表示输出图像的亮度值,对应于输入图像中的亮度值rk。
直方图均衡化函数histeq语法
g = histeq(f, nlev)
其中,f为输入图像,nlev为输出图像指定的灰度级数,默认值64.一般而言,将nlev赋值给灰度级的最大可能数量(通常为256)。
3.3 直方图匹配(规定化)
生成具有指定直方图的图像的方法称为直方图匹配或直方图规定化。
令r和z分别表示输入图像和输出图像的灰度级,输入灰度级的PDF为pr( r ),输出灰度级的PDF为pz(z),我们知道变换为
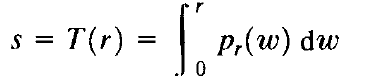
时,导致了有着均衡化概率密度函数ps(s)的灰度级s。现定义一个变量z,表示我们要得到的灰度级为z的输出图像,且具有指定的概率密度函数pz(z)(该直方图具有单位面积且其所有值非负),设该变量满足
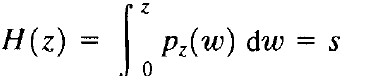
由以上两个等式可得
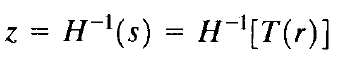
工具箱使用函数histeq的如下形式实现直方图匹配:
g = histeq(f, hspec)
其中,f为输入图像,hspec为指定的直方图(一个由指定值构成的行向量),g为输出图像,其直方图近似于hspec,向量中包含对应于等分空间bin的整数值,histeq的一个特性是在length(hspec)远小于图像f中的灰度级数时,图像g的直方图通常会较好地匹配hspec。
3 空间滤波
3.1 线性空间滤波
使用函数imfilter
imfilter(f, w, filtering_mode, boundary_options, size_options)
其中,f是输入图像,w为滤波掩模,g为滤波结果,filtering_mode用于指定在滤波中使用'corr'(相关)还是'conv'(卷积)。boundary_options用于处理边界充零问题,边界的大小由滤波器大小确定。size_options可以是'same'(保持原来尺寸一样)或'full'(充零之后的尺寸)。
在实现IPT标准线性空间滤波时,会适应到函数imfilter的通用语法:
g = imfilter(f, w, 'replicate')
| 选项 | 描述 |
|---|---|
| 滤波类型 | |
| ‘corr’ | 滤波通过相关完成,默认值 |
| ‘conv’ | 滤波通过卷积完成 |
| 边界选项 | |
| P | 输入图像的边界通过值P来填充扩展,默认值0 |
| ‘replicate’ | 图像大小通过复制外边界的值来扩展 |
| ‘symmetric’ | 图像大小通过镜像反射其边界来扩展 |
| ‘circular’ | 图像大小通过将图像看成是一个二维周期函数的一个周期来扩展 |
| 大小选项 | |
| ‘full’ | 输出图像的大小与被扩展图像的大小相同 |
| ‘same’ | 输出图像的大小与输入图像的大小相同,可以通过将滤波掩模的中心点的偏移限制到原图像中包含的点来实现,默认值 |
3.2 非线性空间滤波
非线性滤波一般有两个函数,nlfilter函数直接执行二维操作,colfilt函数以列的形式组织数据,虽然后者占有更多内存,但是执行速度比前者快,所以更多采用后者,其语法为:
g = colfilt(f, [m, n], 'sliding', @fun, parameters)
其中,m和n也是滤波区域的维数,‘sliding’表示处理过程是在输入图像f中逐个像素地滑动该m*n区域,@fun引用一个函数,parameters表示函数fun可能需要的参数(逗号分隔开)。对于一个大小为M * N的图像f和一个大小为m * n的邻域,函数colfilt生成一个最大尺寸为mn * MN的矩阵A,在该矩阵中,每一列对应于其中心位于图像内某个位置的邻域所包围的像素。
基于矩阵A的组织形式,函数fun
必须分别对矩阵的每一列操作,并返回一个包含所有列的结果的行向量v。v的第k个元素表示的是对A中的第k列进行fun操作后的结果,因而,A中可以有MN列,v的最大维数为1*MN。在使用colfilt之前,输入图像必须经过填充,为此使用函数padarray,语法为:
fp = padarray(f, [r c], method, direction)
其中,f是输入图像,fp是填充后的图像,[r c]用于给出填充f的行数和列数,method和direction的含义如下表:
| 选项 | 描述 |
|---|---|
| method | |
| ‘replicate’ | 图像大小通过复制外边界的值来扩展 |
| ‘symmetric’ | 图像大小通过镜像反射其边界来扩展 |
| ‘circular’ | 图像大小通过将图像看成是一个二维周期函数的一个周期来扩展 |
| direction | |
| ‘pre’ | 在每一维的第一个元素前填充 |
| ‘post’ | 在每一维的最后一个元素后填充 |
| ‘both’ | 在每一维的第一个元素前和最后一个元素后填充,默认值 |
例:
f = [1 2; 3 4];
fp = padarray(f, [3 2], 'replicate', 'post');
得到的fp为

fp = padarray(f, [3 2], 'symmetric', 'post')得到
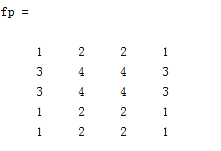
fp = padarray(f, [3 2], 'circular', 'post')得到
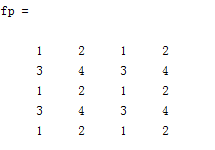
使用例程:
function v = gmean(A)
% V = GMEAN(A)实现对大小为m * n的邻域求几何平均
% 大小为m * n的邻域的几何平均是邻域内亮度值的乘积的 1/mn 次幂
% 使用colfillt实现非线性空间滤波% 返回行数,即获取矩阵A列向量的长度
mn = size(A, 1);
% prod(A, DIM),沿维度DIM进行求乘积,Dim = 1,即对每一列求乘积,相当于prod(A(:,:))
v = prod(A, 1) .^ (1/mn);% 在命令行窗口测试范例
% f = imread('1.jpg');
% f = rgb2gray(f);
% f = im2double(f);
% f = padarray(f, [5 7], 'replicate');
% g = colfilt(f, [5 7], 'sliding', @gmean);
% imshow(f),figure, imshow(g)
4 图像处理工具箱的标准空间滤波器
4.1 线性空间滤波器
fspecial函数,用来生成滤波掩模w,语法是
w = fspecial('type', parameters)
其中,‘type’表示滤波器类型,‘parameters’进一步定义了指定的滤波器,具体如下:
| 类型 | 描述 |
|---|---|
| ‘average’ | fspecial(‘average’, [r c]) 。大小为 rc 的一个矩形平均滤波器。默认值是33,若只有一个数表示[r c]则表示方形滤波器 |
| ‘disk’ | fspecial(‘disk’, r) 。一个圆形平均滤波器(包含在2r+1大小的正方形内),半径为r,默认值5 |
| ‘gaussian’ | fspecial(‘gaussian’, [r c], sig)。一个大小为 r * c 的高斯低通滤波器,标准偏差为sig(正),默认值为 3 * 3 和 0.5 |
| ‘laplacian’ | fspecial(‘laplacian’, alpha)。一个大小为 3 * 3 的拉普拉斯滤波器,其形状由 alpha 指定,范围是 [0, 1] ,默认值0.5 |
| ‘log’ | fspecial(‘log’, [r c], sig)。一个大小为 r * c 的高斯-拉普拉斯滤波器,标准偏差是sig(正),默认值是 5 * 5 和 0.5,若用一个值表示[r c]表示方阵 |
| ‘motion’ | fspecial(‘motion’, len, theta)。围绕一幅有着len个像素的图像线性运动时,输出一个滤波器,运动方向是theta,单位是度,即从水平方向逆时针转动的角度,默认值是9和0,表示沿水平方向9个像素的运动 |
| ‘prewitt’ | fspecial(‘prewitt’)。输出一个大小是 3 * 3 的Prewitt掩模wv,它近似于垂直梯度。水平梯度掩模可以通过置换结果wh = wv ‘ 获得 |
| ‘sobel’ | fspecial(‘sobel’)。输出一个3 * 3 的Sobel掩模sv,它近似于垂直梯度。水平梯度掩模可以通过置换结果sh = sv ‘ 获得 |
| ‘unsharp’ | fsepcial(‘unsharp’, alpha)。输出一个大小为3 * 3的非锐化滤波器,参数alpha控制形状,范围是[0 1],默认值0.2 |
例,下面我们使用一个拉普拉斯滤波器来增强一幅图像,说明 fspecial 和 imfilter 函数的用法。图像 f(x, y)的拉普拉斯算子定义为

该二阶导数的通用数字近似为

因而有
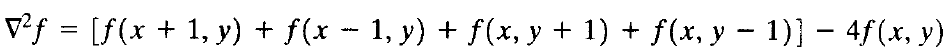
通过对图像和下面的空间掩模做卷积操作
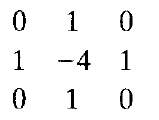
或考虑对角线元素,使用如下掩模
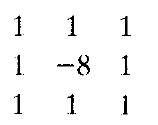
使用拉普拉斯算子增强图像的基本公式有:
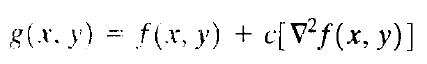
其中f(x, y)为输入图像,g(x, y)为增强后的图像,若掩模的中心系数为正,则c为1,否则为-1。由于拉普拉斯算子是微分操作符,所以它会使图像锐化,并且使常量区域为0,所以在原图像中添加黑色会还原灰度级色调。
函数fspecial(‘laplacian’, alpha)实现一个更为常见的拉普拉斯算子掩模:

该掩模可对增强结果进行精细的调整。
f = imread('1.jpg');
f = im2double(f);
w = fspecial('laplacial', 0);
g = f - imfilter(f, w, 'replicate');
% 原图像减去滤波之后的图像即增强后的图像
imshow(g)4.2 非线性空间滤波
ordfilt2函数用于生成非线性空间滤波器——统计排序滤波器,也称排序滤波器,其响应基于对图像邻域中所包含的像素进行排序,然后使用排序结果确定的值来替代邻域中的中心像素的值。其语法是:
g = orfilt2(f, order, domain)
即,使用邻域的一组排序元素中的第order个元素来替代f中的每个元素,而该邻域则由domain中的非零元素指定。这里,domain是一个由0和1组成的大小为m * n的矩阵,该矩阵指定了将在计算中使用的邻域中的像素位置。
要实现大小为m * n的最小滤波器,可使用语法
g = orfilt2(f, 1, ones(m, n))
在该语句中,1表示mn个样本中的第一个样本,ones(m, n)创建了一个元素值为1、大小为m * n的矩阵,表明邻域内的所有样本都将用于计算。
相应地还有最大滤波器,可用语法:
g = orfilt2(f, m*n, ones(m, n))
中值滤波器语法:
g = ordfilt2(f, median(1:m*n), ones(m, n))
其中median(1:m*n)简单地计算排序序列1,2,···,mn的中值,函数median的通用语法是:
v = median(A, dim)
其中,v是向量,它的元素是A沿着维数dim的中值,例如,当dim = 1时,则v的每个元素都是矩阵A中沿相应列的元素的中值。
二维中值滤波函数:
g = medfilt2(f, [m n], padopt)
数组[m n]定义了一个大小为 m * n 的邻域,默认3 * 3中值就在该邻域上计算,而padopt指定了三个可能的边界填充选项之一:
| 选项 | 描述 |
|---|---|
| ‘zero’ | 默认值,填充0 |
| ‘indexed’ | 若f是double类图像,则以 1来填充,否则以0来填充图像 |
| ‘symmetric’ | 图像大小通过镜像反射其边界来扩展 |
函数默认形式为
g = medfilt2(f)
表示一个大小为3 * 3的邻域来计算中值,并用0来填充图像边界。
这篇关于冈萨雷斯Matlab版第三章(亮度变换与空间滤波)知识点要点记录的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








