【智能算法】流向算法（FDA）原理及实现

本文主要是介绍【智能算法】流向算法（FDA）原理及实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

1.背景

2021年，H Karami等人受到水流运动规律启发，提出了流向算法（Flow Direction Algorithm， FDA）。

2.算法原理

2.1算法思想

FDA受到了流入排水池的水流的启发，模拟了水流朝向排水池最低高度出口的方向流动 (水往低处流~)。首先创建一个初始种群在排水池即问题的搜索空间中，然后考虑了邻近水流及其坡度对水流的影响，最后使水流流向海拔较低的位置，也就是排水池的最低海拔出口点（适应度值度量）。

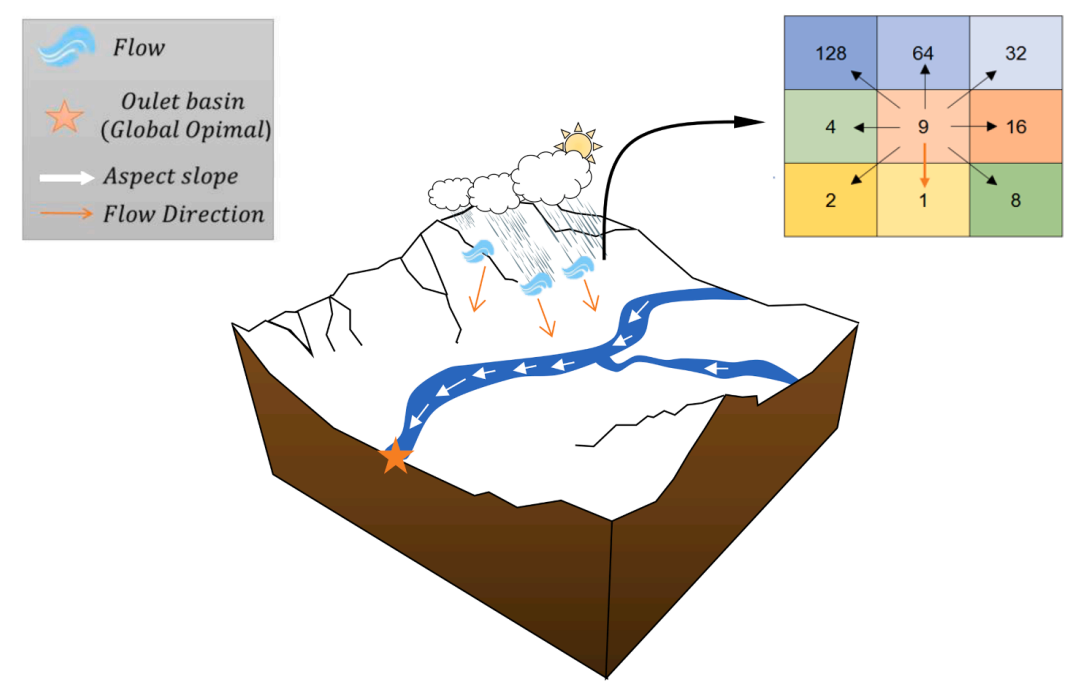
2.2算法过程

创建水流领域：

FDA 假设每个水流附近存在 β 个邻域，则第i个水流的第j个邻居位置为:
$$N\left(j\right)=F\left(i\right)+R_{\mathbb{N}}\times \Delta \text{\hspace{1em}(1)}$$
其中，RN是均值为0，标准差为1的正态分布随机数；Δ 是用来控制算法搜索空间大小的控制参数，其值越小算法搜索范围越小，反之搜索空间越大．Δ的值从一个较大值线性减小到较小值，并朝向随机位置以增加多样性，表述为：
$$\begin{array}{rl}\Delta & =[R\times X_{\mathrm{rand}}-R\times F(i)]\times \Vert X_{\mathrm{best}}-F(i)\Vert \times W\end{array}\text{\hspace{1em}(2)}$$
其中，Xrand为随机水流位置，Xbest为当代最优水流位置，W为非线性权重：
$$W={\left(1-\frac{\tau }{{\tau }_{\max }}\right)}^{2\times R_N}\times \left(R_{\mathrm{u}}\times \frac{\tau }{{\tau }_{\max }}\right)\times R_{\mathrm{u}}\text{\hspace{1em}(3)}$$
其中，τ 和 τmax分别为当前迭代次数和最大迭代次数，Ru为均匀分布的随机向量。
更新水流位置：
FDA算法中水流流向海拔最低的方向，若最优邻居N(k)的适应度fN(k)小于当前水流的适应度fF(i)，则当前水流流向该邻居，此时新的水流位置为：
$${\mathbf{F}}_{\mathrm{new}}(i)=\mathbf{F}(i)+v\frac{\mathbf{F}(i)-\mathbf{N}(k)}{\Vert \mathbf{F}(i)-\mathbf{N}(k)\Vert }\text{\hspace{1em}(4)}$$
其中，k为最优邻居的序号；v为水流速度，与坡度直接相关:
$$v=R_{\text{N}}\times S_0(i,k,D)\text{\hspace{1em}(5)}$$
其中，S0(i,k,D)为最优邻居N(k)和水流F(i)位置之间的斜率为:
$$S_0(i,k,D)=\frac{f_{\mathbf{F}(i)}-f_{\mathbf{N}(k)}}{\Vert F(i,d)-N(k,d)\Vert }\text{\hspace{1em}(6)}$$
如果随机水流的适应度优于当前水流的适应度，那么当前水流将沿着随机水流的方向流动。
$${\mathbf{F}}_{\mathrm{new}}(i)=\mathbf{F}(i)+R_{\mathrm{N}}\times \left[\mathbf{F}(r)-\mathbf{F}(i)\right]\text{\hspace{1em}(7)}$$
如果当前水流的适应度优于其最优邻居的适应度，根据适应度值来决定当前水流是沿着该随机水流的方向移动，还是沿着最优水流的方向移动。
$${\mathbf{F}}_{\mathrm{new}}(i)=\mathbf{F}(i)+2R_{\mathrm{N}}\times \left[{\mathbf{X}}_{\mathrm{best}}-\mathbf{F}(i)\right]\text{\hspace{1em}(8)}$$

流程图：

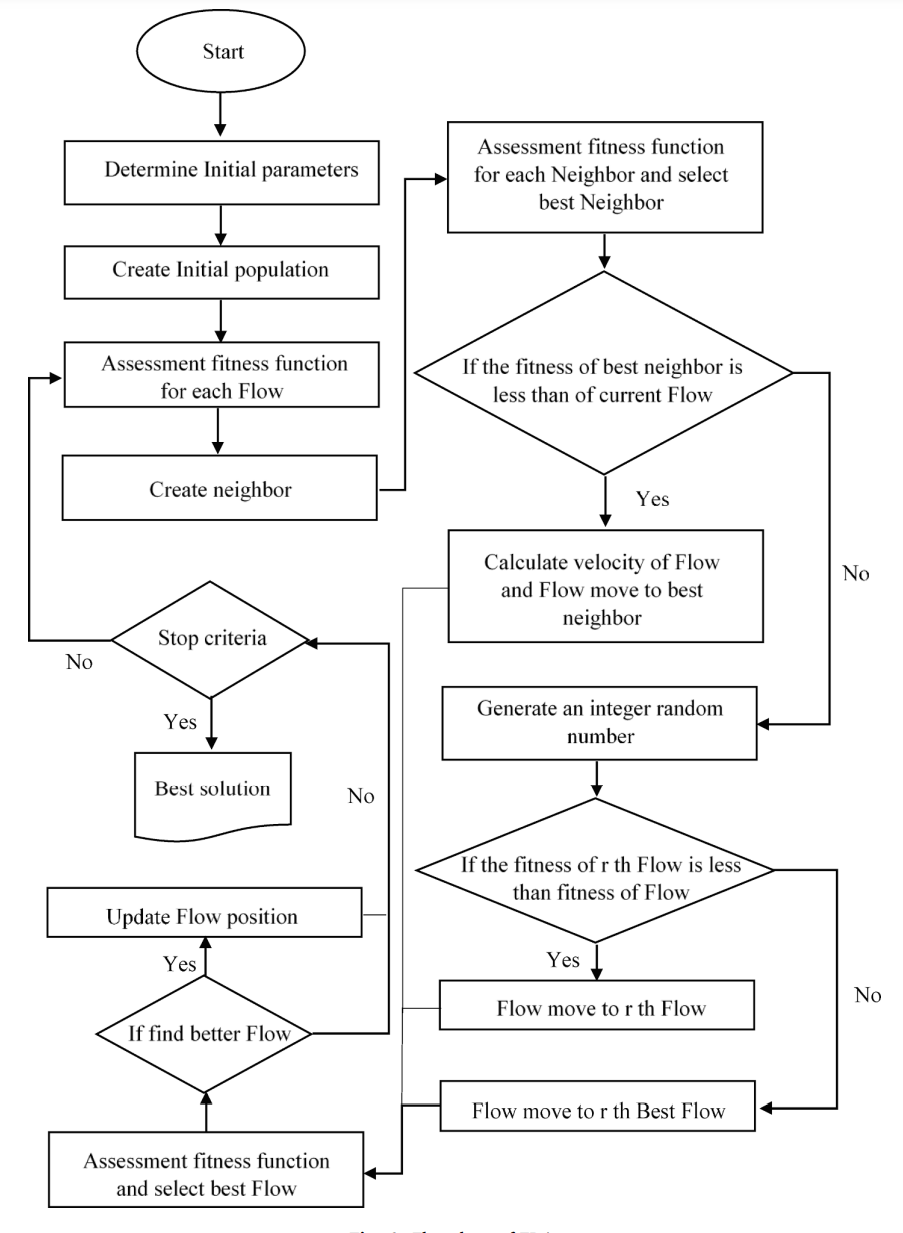
3.结果展示

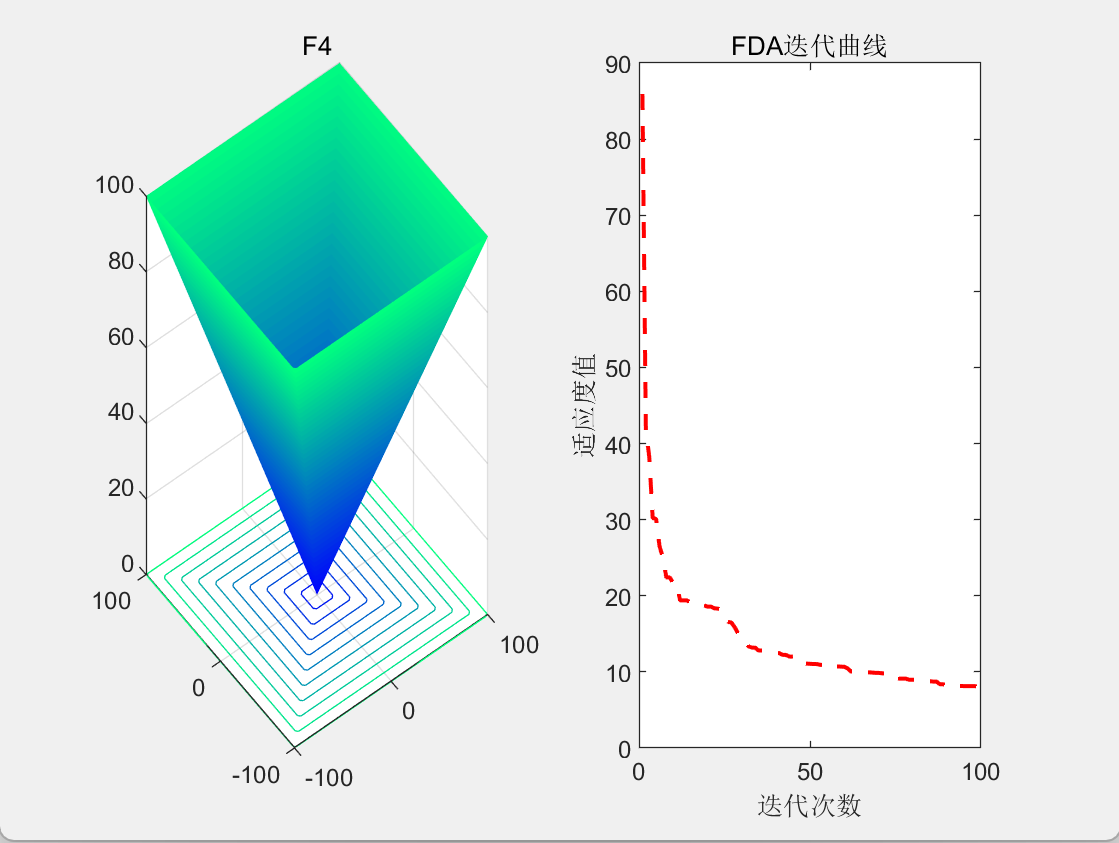
4.参考文献

[1] Karami H, Anaraki M V, Farzin S, et al. Flow direction algorithm (FDA): a novel optimization approach for solving optimization problems[J]. Computers & Industrial Engineering, 2021, 156: 107224.

这篇关于【智能算法】流向算法（FDA）原理及实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---