本文主要是介绍数字IC前端学习笔记:数字乘法器的优化设计(基4布斯编码华莱士树乘法器),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
相关阅读
数字IC前端![]() https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
使用基2布斯乘法器虽然能减少乘数中0的数量,但最终还是无法减少部分积的数量,因此一种更合理的编码方式产生了——基4布斯编码。它可以将部分积的数量减少一半,本文中还会使用华莱士树结构对部分积进行压缩,进一步提高其性能。
基4布斯编码的推导和基2布斯编码类似,首先同样把乘数展开为2的幂之和形式。
基4布斯编码的基系数为,上式可改写为:
编码规则变成了从开始每次检查三位,注意,第二个被检查的位是
,所以设计要求被乘数包括符号位为偶数位,如果不满足,则需要符号拓展一位以适应编码规则。根据上述推导,总结得到的基4布斯编码规则如下表1所示。
表1 补码的基4布斯编码规则
| Xn+1 | Xn | Xn-1 | Code | BRCn+1 | BRCn | 值 | 被乘数操作 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 左移两位 |
| 0 | 0 | 1 | 1 | 0 | 1 | +1 | 相加,左移两位 |
| 0 | 1 | 0 | 2 | 0 | 1 | +1 | 相加,左移两位 |
| 0 | 1 | 1 | 3 | 1 | 0 | +2 | 左移一位,相加,左移一位 |
| 1 | 0 | 0 | 4 | 1 | 0 | -2 | 左移一位,相减,左移一位 |
| 1 | 0 | 1 | 5 | 0 | 1 | -1 | 相减,左移两位 |
| 1 | 1 | 0 | 6 | 0 | 1 | -1 | 相减,左移两位 |
| 1 | 1 | 1 | 7 | 0 | 0 | 0 | 左移两位 |
将相邻三位编码成两位,每位可以是1、1和0,其实也可以编码成一位,这样每位就可以是0、1、2、1、2,最后结果的处理都是一样的。
乘法器每次检查乘数的三个位,并决定执行以下操作之一:
- 被乘数相加并左移两位。
- 被乘数左移一位,相加,再左移一位。
- 被乘数相减(加上被乘数相反数的补码),并左移两位。
- 被乘数左移两位。
作为基4布斯编码的一个例子,下图1给出了十进制-65的基4布斯编码。

图1 十进制数(-65)基4布斯编码
基4布斯编码华莱士树乘法器由三部分组成,基4布斯编码模块、部分积产生模块和最后的华莱士树累加结构。下面分别介绍它们的详细组成。
基4布斯编码模块的接口方框图如图2所示,布斯编码模块对每三位乘数进行布斯编码,因此对于八位的数据宽度,设计需要四个编码模块,输出为四个信号,分别是表示减操作的Neg信号,表示部分积为零、部分积两倍和一倍的Zero、Two和One信号。这些信号被提供给部分积产生模块,随后部分积产生模块将根据这些信息输出正确的部分积。
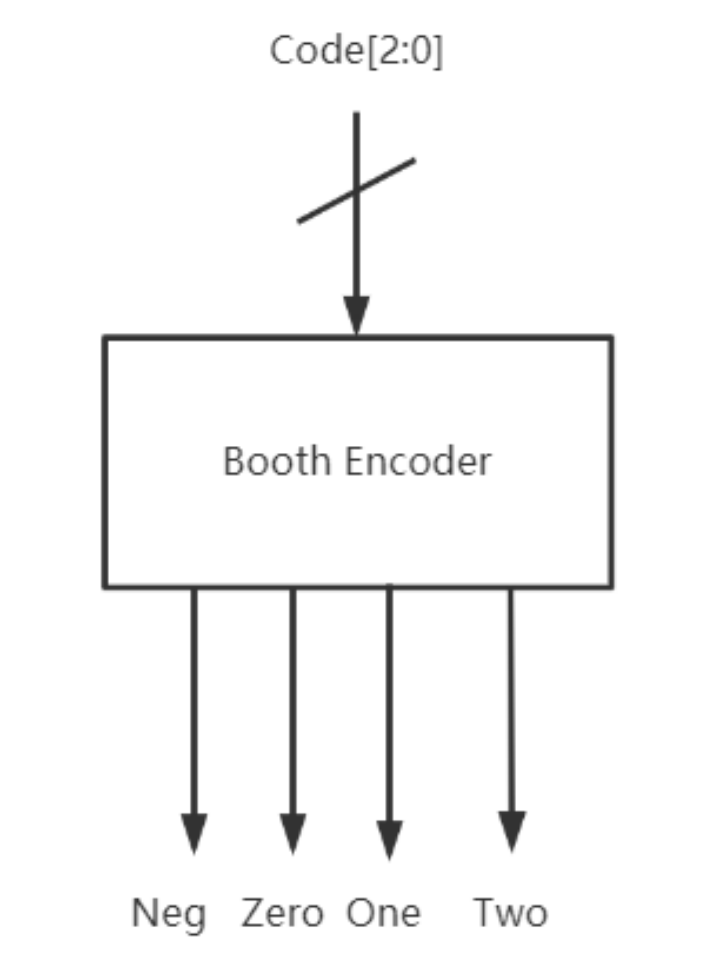
图2 基4布斯编码模块
部分积产生模块的方框接口图如图3所示。部分积产生模块的方框接口图如图3所示。它根据不同的控制信号和被乘数产生特定的部分积形式。注意,作为一种最简单的实现形式,为了保证补码运算的统一性和正确性,设计只需要将所有输入模块的被乘数负号拓展至乘积结果的位宽即可(这其实也可通过一些算法来优化)。

图3 部分积产生模块
注意,这里的部分积只在从乘数的包括最低位在内的间隔一位产生,因此所有部分积的会错开两位,这与之前的部分积的规律不同。
例如表2表示了两个八位数使用基4布斯编码相乘的过程。可以看到对于八位数据,使用基4布斯编码只产生了四行部分积,是不使用编码部分积行数的一般,乘法器的速度很大情况下取决于部分积的深度而不是最后的向量合成。
表2 基4布斯编码的部分积产生和累加过程
| A | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 7 | ||||||||
| ×B | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 9 | |||||||||
| 0 | 1 | -2 | 1 | Radix 4 Booth | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1*2^0*A | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | -2*2^2*A | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1*2^4*A | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0*2^6*A | ||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 63 |
根据华莱士树构建的规则,部分积的构建过程为第一阶段使用两个半加器、十二个全加器压缩前三行部分积,第一行低两位无需压缩直接得到结果低两位,第三列的和也可以直接被当做结果的第三位。第二阶段使用三个半加器,十个全加器对最后的三行压缩,此时乘积的第四位也可得到。最后使用向量合成器对高十二位的两个数进行相加,即可得到最后结果。
具体的Verilog代码实现见附录,Modelsim软件仿真截图如图4所示。使用Synopsis的综合工具Design Compiler综合的结果如图3所示,综合使用了0.13μm工艺库。
 图4 基4布斯编码华莱士树乘法器仿真结果
图4 基4布斯编码华莱士树乘法器仿真结果
 图5 基4布斯编码华莱士树乘法器综合结果
图5 基4布斯编码华莱士树乘法器综合结果
在Design Compiler中使用report_timing命令,可以得到关键路径的延迟,如图6所示,可以看出延迟有4.24ns。

图6 基4布斯编码华莱士树乘法器关键路径报告
在Design Compiler中使用report_area命令,报告所设计电路的面积占用情况,如图7所示。
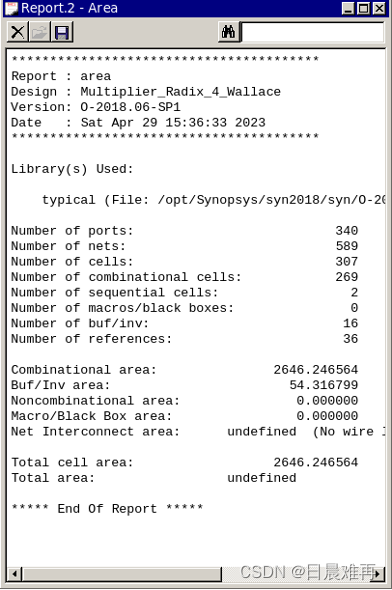
图7 基4布斯编码华莱士树乘法器面积报告
基4布斯编码华莱士树乘法器的Verilog代码如下所示。
module Booth_Encoder(
input [2:0] Code,
output Neg,Zero,One,Two
);assign Neg = Code[2];assign Zero = (Code == 3'b000) || (Code == 3'b111);assign Two = (Code == 3'b100) || (Code == 3'b011);assign One = (!Zero) & (!Two);endmodulemodule Partial_Generater(
input [7:0] Multiplicand,
input Neg,Zero,One,Two,
output [15:0] Partial_Product);reg [15:0]Partial_Tmp;always@(*) beginPartial_Tmp=16'b0;if(Zero)Partial_Tmp=16'b0;else if(One)Partial_Tmp={{8{Multiplicand[7]}},Multiplicand};else if(Two)Partial_Tmp={{7{Multiplicand[7]}},Multiplicand,1'b0};endassign Partial_Product = Neg?(~Partial_Tmp+1'b1) : Partial_Tmp;endmodulemodule Adder_half (input Mult1,input Mult2,output Res,output Carry
);assign Res = Mult1 ^ Mult2;assign Carry = Mult1 & Mult2;endmodulemodule Adder (input Mult1,input Mult2,input I_carry,output Res,output Carry
);assign Res = Mult1 ^ Mult2 ^ I_carry;assign Carry = (Mult1 & Mult2) | ((Mult1 ^ Mult2) & I_carry);endmodulemodule Multiplier_Radix_4_Wallace(input [7:0] A ,input [7:0] B ,output [15:0] Sum
);//A Multiplicand //B Multiplierwire Neg[3:0];wire Zero[3:0];wire One[3:0];wire Two[3:0];wire [15:0]Partial_Product[3:0];wire [15:0]Partial_Product_t[3:0];wire [13:0]Result_0;wire [12:0]Carry_0;wire [12:0]Result_1;wire [12:0]Carry_1;//Booth_EncoderBooth_Encoder Booth_Encoder_0({B[1:0],1'b0},Neg[0],Zero[0],One[0],Two[0]);Booth_Encoder Booth_Encoder_1({B[3:1]},Neg[1],Zero[1],One[1],Two[1]);Booth_Encoder Booth_Encoder_2({B[5:3]},Neg[2],Zero[2],One[2],Two[2]);Booth_Encoder Booth_Encoder_3({B[7:5]},Neg[3],Zero[3],One[3],Two[3]);//Partial_GeneraterPartial_Generater Partial_Generater_0(A,Neg[0],Zero[0],One[0],Two[0],Partial_Product_t[0]);Partial_Generater Partial_Generater_1(A,Neg[1],Zero[1],One[1],Two[1],Partial_Product_t[1]);Partial_Generater Partial_Generater_2(A,Neg[2],Zero[2],One[2],Two[2],Partial_Product_t[2]);Partial_Generater Partial_Generater_3(A,Neg[3],Zero[3],One[3],Two[3],Partial_Product_t[3]);assign Partial_Product[0]=Partial_Product_t[0];assign Partial_Product[1]=Partial_Product_t[1]<<2;assign Partial_Product[2]=Partial_Product_t[2]<<4;assign Partial_Product[3]=Partial_Product_t[3]<<6;//Wallace_Tree//Stage1assign Sum[0]=Partial_Product[0][0];assign Sum[1]=Partial_Product[0][1];Adder_half Adder_half_0(Partial_Product[0][2],Partial_Product[1][2],Result_0[0],Carry_0[0]);Adder_half Adder_half_1(Partial_Product[0][3],Partial_Product[1][3],Result_0[1],Carry_0[1]);Adder Adder_0(Partial_Product[0][4],Partial_Product[1][4],Partial_Product[2][4],Result_0[2],Carry_0[2]);Adder Adder_1(Partial_Product[0][5],Partial_Product[1][5],Partial_Product[2][5],Result_0[3],Carry_0[3]);Adder Adder_2(Partial_Product[0][6],Partial_Product[1][6],Partial_Product[2][6],Result_0[4],Carry_0[4]);Adder Adder_3(Partial_Product[0][7],Partial_Product[1][7],Partial_Product[2][7],Result_0[5],Carry_0[5]);Adder Adder_4(Partial_Product[0][8],Partial_Product[1][8],Partial_Product[2][8],Result_0[6],Carry_0[6]);Adder Adder_5(Partial_Product[0][9],Partial_Product[1][9],Partial_Product[2][9],Result_0[7],Carry_0[7]);Adder Adder_6(Partial_Product[0][10],Partial_Product[1][10],Partial_Product[2][10],Result_0[8],Carry_0[8]);Adder Adder_7(Partial_Product[0][11],Partial_Product[1][11],Partial_Product[2][11],Result_0[9],Carry_0[9]);Adder Adder_8(Partial_Product[0][12],Partial_Product[1][12],Partial_Product[2][12],Result_0[10],Carry_0[10]);Adder Adder_9(Partial_Product[0][13],Partial_Product[1][13],Partial_Product[2][13],Result_0[11],Carry_0[11]);Adder Adder_10(Partial_Product[0][14],Partial_Product[1][14],Partial_Product[2][14],Result_0[12],Carry_0[12]);Adder Adder_11(Partial_Product[0][15],Partial_Product[1][15],Partial_Product[2][15],Result_0[13],);//Stage2assign Sum[2]=Result_0[0];assign Sum[3]=Result_1[0];Adder_half Adder_half_2(Carry_0[0],Result_0[1],Result_1[0],Carry_1[0]);Adder_half Adder_half_3(Carry_0[1],Result_0[2],Result_1[1],Carry_1[1]);Adder_half Adder_half_4(Carry_0[2],Result_0[3],Result_1[2],Carry_1[2]);Adder Adder_12(Carry_0[3],Result_0[4],Partial_Product[3][6],Result_1[3],Carry_1[3]);Adder Adder_13(Carry_0[4],Result_0[5],Partial_Product[3][7],Result_1[4],Carry_1[4]);Adder Adder_14(Carry_0[5],Result_0[6],Partial_Product[3][8],Result_1[5],Carry_1[5]);Adder Adder_15(Carry_0[6],Result_0[7],Partial_Product[3][9],Result_1[6],Carry_1[6]);Adder Adder_16(Carry_0[7],Result_0[8],Partial_Product[3][10],Result_1[7],Carry_1[7]);Adder Adder_17(Carry_0[8],Result_0[9],Partial_Product[3][11],Result_1[8],Carry_1[8]);Adder Adder_18(Carry_0[9],Result_0[10],Partial_Product[3][12],Result_1[9],Carry_1[9]);Adder Adder_19(Carry_0[10],Result_0[11],Partial_Product[3][13],Result_1[10],Carry_1[10]);Adder Adder_20(Carry_0[11],Result_0[12],Partial_Product[3] [14],Result_1[11],Carry_1[11]);Adder Adder_21(Carry_0[12],Result_0[13],Partial_Product[3][15],Result_1[12],);assign Sum[15:4]=Result_1[12:1]+Carry_1[11:0];
endmodule
这篇关于数字IC前端学习笔记:数字乘法器的优化设计(基4布斯编码华莱士树乘法器)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




