本文主要是介绍基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵
目录
前言
一、Givens旋转简介
二、Givens旋转解释
三、Givens旋转进行QR分解
四、Givens旋转进行QR分解数值计算例子
五、求逆矩阵
六、MATLAB仿真
七、参考资料
总结
前言
在进行QR分解时,HouseHolder变换一次将一个向量除第一个元素以外都转化成零。而有一种方法,可以每次将向量的一个元素转化成0,也可以最终达到正交化的目的,它就是Givens旋转。Givens旋转矩阵是正交矩阵,使用Givens旋转很容易就可以将一个向量的某个分量的某个指定分量化为0。本文会通过列举例子说明如何将一个矩阵通过Givens旋转分解为Q矩阵和R矩阵,最后,会用MATLAB进行仿真,当然,代码也会分享出来。
提示:以下是本篇文章正文内容,希望能帮助到各位,转载请附上链接。
一、Givens旋转简介
Givens旋转矩阵是正交矩阵,使用Givens旋转很容易就可以将一个向量的某个分量的某个指定分量化为0。
本文中主要考虑实数的情况。
2×2的Givens旋转矩阵如下:
其中
那么就可以将向量旋转到x轴上面去,如下图所示。当然改变正余弦函数也能旋转到y轴上面去。
即
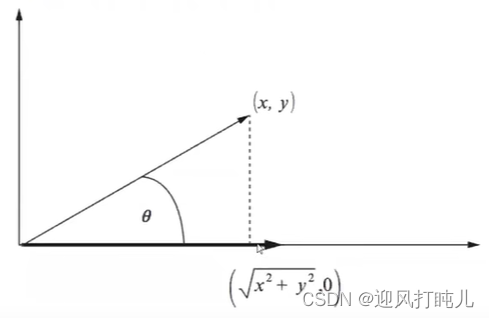
可以把简写三角函数,如下所示
二、Givens旋转解释
我们将向量看成一个复数,即
则
将其也看成一个复数
对比和
,学过复数的话,显然就能看出这是顺时针旋转了
的角度。
三、Givens旋转进行QR分解
下面我们来说明如何通过Givens旋转来实现QR分解。其实原理很简单,就是通过将原矩阵A的主对角线下方的元素都通过Givens旋转置换成0,形成上三角矩阵R,同时左乘的一系列Givens矩阵相乘得到一个正交阵Q。
如下图所示,G(m,n)是Givens旋转矩阵,相当于用某一列的第m个元素去将第n个元素清零。

也可以通过下图来理解,其中×表示没有发生变化的元素,m表示值改变的元素,每一个向右的箭头表示原矩阵左乘了1次Givens矩阵。

由上图我们会发现清一个0时只影响两行,所以对一个高阶矩阵,在清某一列的几个0时可以同时执行,加快计算速度。比如对于4×4阶矩阵,可以在选第1列的第1个元素去将第一列的第2个元素清零的同时,也选择第1列的第3个元素去将第一列的第4个元素清零。
四、Givens旋转进行QR分解数值计算例子
设矩阵,用Givens旋转的方法对其进行QR分解。
解:由于其第1列的第2个元素已经为0了,不用对它进行消0操作,我们首先用第1列的第1个元素对第1列的第3个元素清0。
易求
则Givens矩阵可写为
所以
接下来对上面结果右下角的四个元素进行Givens旋转,用3去将-4消为0。
易求
则Givens矩阵可写为
所以
所以
所以
故
五、求逆矩阵
分解得到Q矩阵和R矩阵后可参考下面两篇文章进行求逆矩阵:
施密特正交化QR分解求逆矩阵与MATLAB仿真:http://t.csdnimg.cn/d1IGR
一种基于约化因子上三角矩阵求逆方法与MATLAB仿真:http://t.csdnimg.cn/uZJkG
六、MATLAB仿真
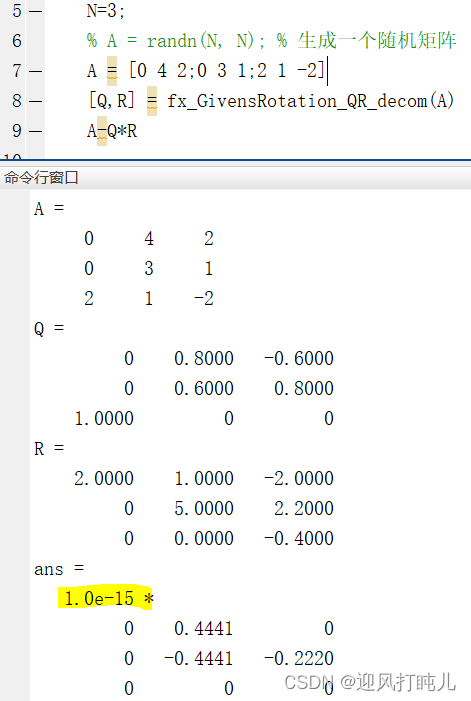
可见,仿真结果和上面的数值计算结果吻合。
七、参考资料
参考资料:https://download.csdn.net/download/m0_66360845/89043215
总结
以上就是今天要讲的内容,本文介绍了Givens旋转,在我理解的基础上讲解了它的几何意义,以及怎样用它将可逆矩阵分解成Q矩阵和R矩阵。同时,也用MATLAB验证了Givens旋转 QR分解算法。
这篇关于基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





