数据结构之二叉树由浅入深(三)

本文主要是介绍数据结构之二叉树由浅入深(三)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题外话

正题

第一题

第一题思路

第一题代码

第二题

第二题思路

第二题代码

第三题

第三题思路

第三题代码

第四题

第四题思路

第四题代码

第五题

第五题思路

第五题代码

第六题

第六题思路

第六题代码

第七题

第七题思路

第七题代码

第八题

第八题思路

第八题代码

小结

题外话

让我们继续回到数据结构二叉树的内容,在我前面数据结构文章中已经讲完了二叉树的概念,性质,还做了一些练习题,今天直接写代码

正题

如果家人们对递归很熟练的话,今天内容将会超级无敌巨简单,话不多说3,2,1让我们,上链接(练习题)!!

第一题

获取二叉树结点个数

第一题思路

和二叉树前序遍历差不多,从根节点开始遍历,然后遍历左子树,右子树,如果结点为空直接返回0就可以.

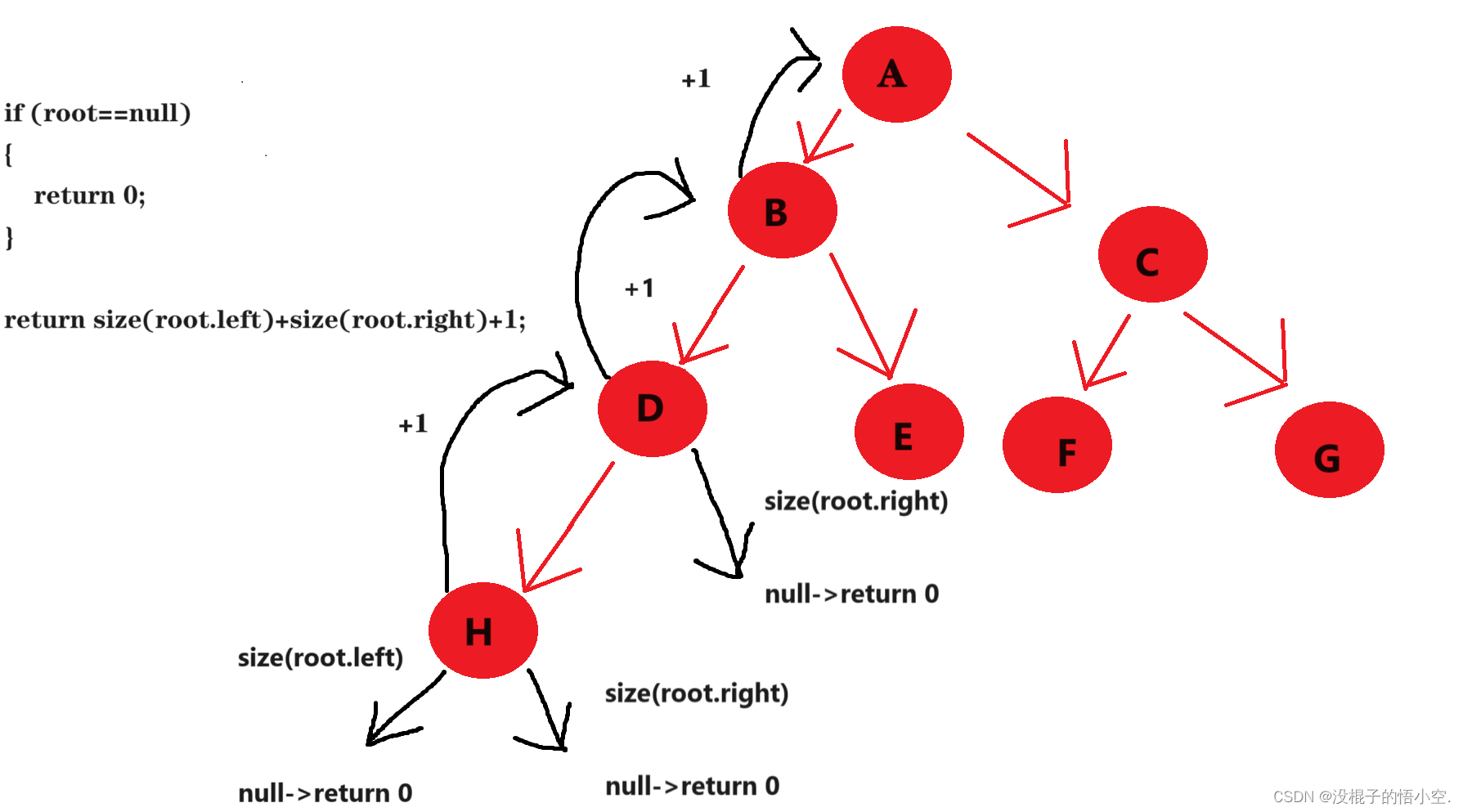
大家可以结合我上面这个图,我画的还是蛮清楚的吧,

左子树右子树走完之后就会+1,很巧妙的一个设计,只要这里理解了,剩下的题都是简简单单

第一题代码

public int size(TreeNode root)
{
//如果结点为空返回0if (root==null){return 0;}
//持续递归,左子树右子树走完就加一return size(root.left)+size(root.right)+1;

}

第二题

获取叶子结点个数

第二题思路

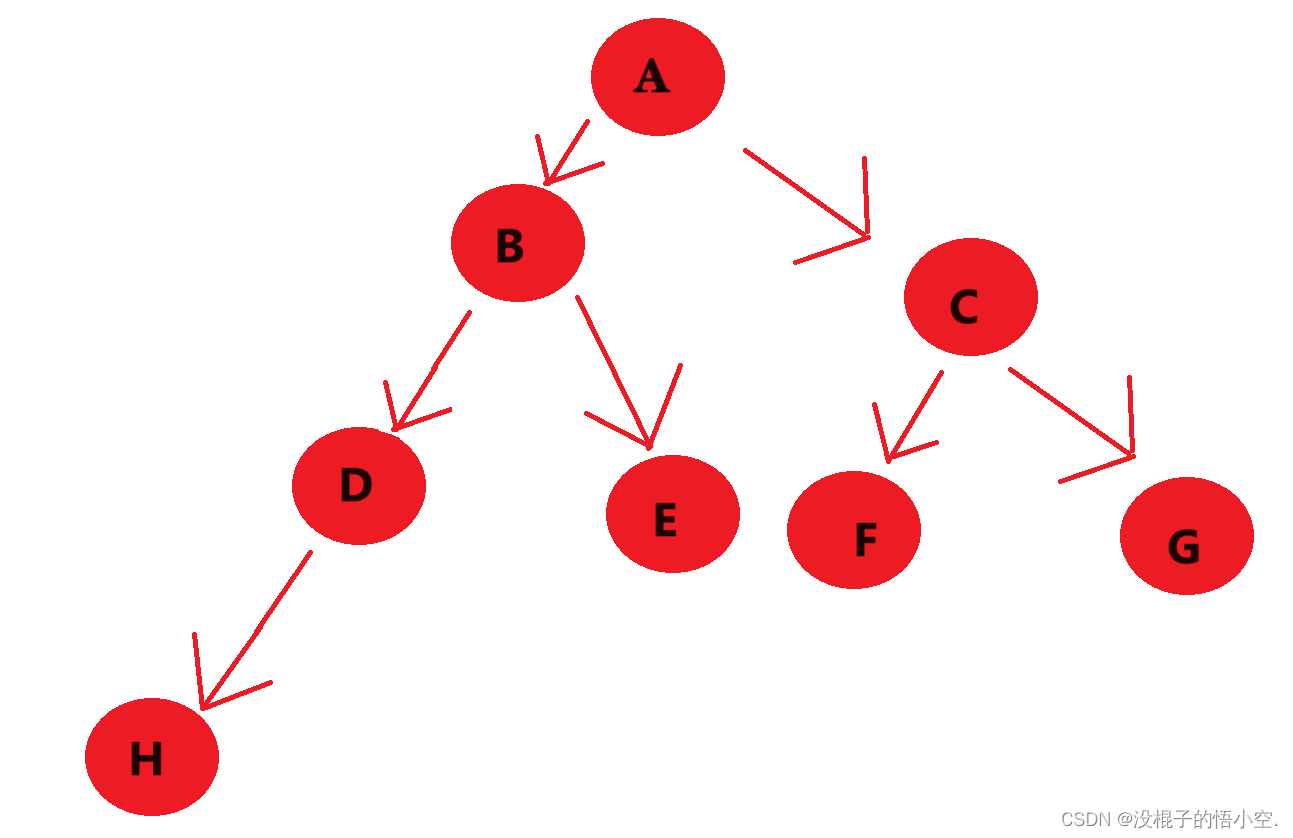
一样是递归的方式,不过可以有两种思路,一种是创建一个计数器,如果一个结点左子树,右子树都为空就让计数器+1,最后返回计数器就可以

另一种更巧妙一点,如果一个结点左子树,右子树都为空,则返回1,最后返回左子树的叶子节点加上右子树的叶子结点即可,如果第一题的递归看懂了,这一题也是手到擒来

我们这里用的是第二种方法

第二题代码

public int getLeafNode(TreeNode root)
{
//如果结点为空返回0if (root==null){return 0;}
//如果左子树右子树都为空,则返回1if (root.left==null&& root.right==null) {return 1;}
//返回左子树叶子树加上右子树叶子树return getLeafNode(root.left)+getLeafNode(root.right);}

第三题

// 获取第K层结点的个数

第三题思路

假设我们要获取第三层结点个数,我们只需要从根结点往下走两层就可以找到第三层结点

所以可以走一层就让k-1,当k==1的时候我们就找到了第三层的结点,直接返回1就可以

最后返回左子树找到的第k层结点加上右子树找到的第k层结点就可以了

(这里也可以用计数器但是我没用它)

第三题代码

public int getKLevelNodeCount(TreeNode root,int k)
{
//这里我除了让root为空返回0
    if (root==null) {return 0;}
//当k==1说明已经遍历第k层结点,直接返回1即可if (k==1){return 1;}
//返回第k层全部结点return getKLevelNodeCount(root.left,k-1)+ getKLevelNodeCount(root.right,k-1);
}

第四题

获取树的高度

第四题思路

我们只需要找到二叉树的左子树和右子树高度的最大值,返回最大值即可

第四题代码

public int getHeight(TreeNode root)
{
//结点为空时返回0if (root==null) {return 0;}
//创建两个变量,记录左子树和右子树的高度int left=getHeight(root.left);int right=getHeight(root.right);
//比较两棵树高度,返回树的最大值加上1(当前结点)return left>right?left+1:right+1;
}

第五题

检测值为value的元素是否存在

第五题思路

递归的方式前序遍历二叉树,找到val,返回即可

注意

找到val意味着没必要再递归了,应该添加条件停止递归

第五题代码

public TreeNode find(TreeNode root,char val)
{
//如果结点为空直接返回该结点if (root==null){return root;}
//如果结点的val等于val,找到了,直接返回rootif (root.val==val){return root;}
//递归左子树TreeNode node1=find(root.left,val);
//如果找到了val,则node1不为空,则返回node1,不要再往下递归了if (node1!=null){return node1;}
//递归右子树TreeNode node2=find(root.right,val);
//如果找到了val,则node2不为空,则返回node2,不要再往下递归了if (node2!=null){return node2;}
//如果整棵树遍历完了也没有找到val,直接返回空return null;}

第六题

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

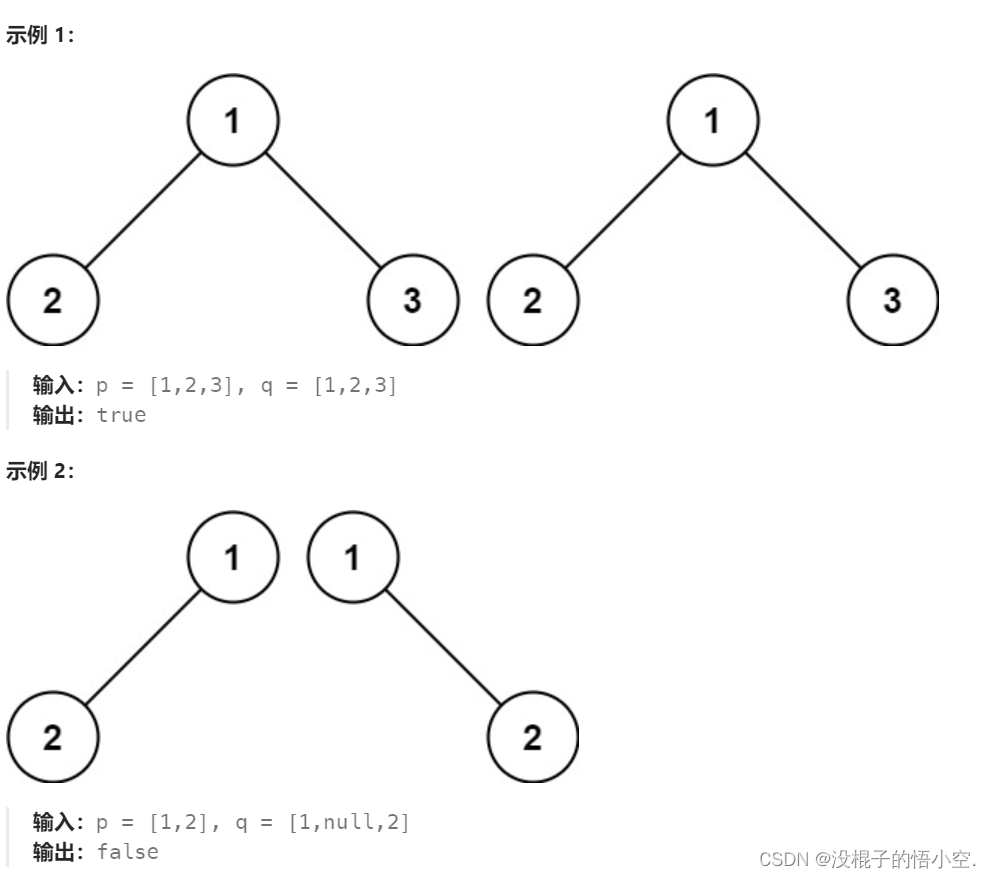
第六题思路

只需要从两颗二叉树根节点开始比较,同时递归左子树右子树并比较即可

注意

除了判断两颗二叉树对应val是否相同,还需要判断两棵二叉树结点为空时的情况

第六题代码

public boolean isSameTree(TreeNode p, TreeNode q) {
//如果其中一颗二叉树为空,另一颗不为空直接返回falseif (p==null&&q!=null||p!=null&&q==null){return false;}
//两颗都为空则返回trueif (p==null&&q==null){return true;}
//如果两颗树对应结点val值不相等直接返回falseif (p.val!=q.val){return false;}//同时递归两棵树的左子树,右子树,当两棵树的左右子树完全相等返回truereturn   isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}

第七题

判断一棵树是不是另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

第七题思路

在第六题的基础上,很容易写出第七题,先判断两棵树根节点是否相同,再判断左子树是否相同,右子树是否相同即可

第七题代码

public boolean isSubtree(TreeNode root, TreeNode subRoot) {
//如果两棵树结点互相匹配的时候有空结点直接返回false,否则再往下走会产生空指针异常if (root==null||subRoot==null){return false;}
//判断两树根节点是否相同if (isSameTree(root,subRoot)){return true;}
//再从左子树判断是否是子树if (isSubtree(root.left,subRoot)){return true;}
//再从右子树判断是否是子树if (isSubtree(root.right,subRoot)){return true;}
//都不相同直接falsereturn false;
}

第八题

翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

第八题思路

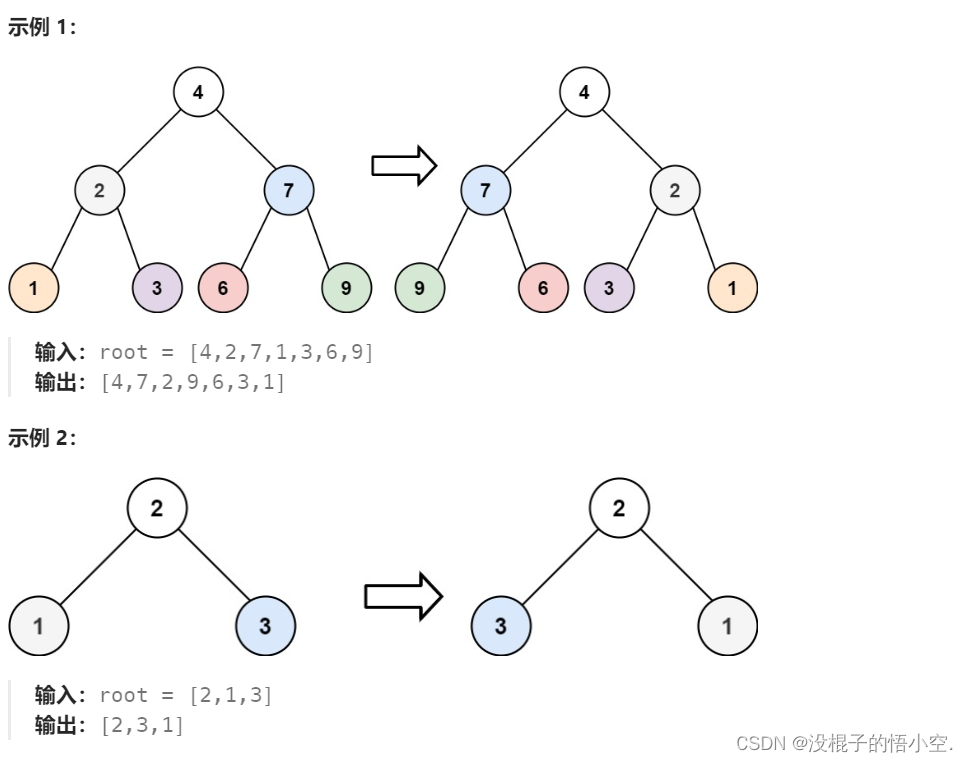
利用递归遍历二叉树,只要结点的左子树和右子树不是全为空,就将两结点交换即可

第八题代码

public TreeNode invertTree(TreeNode root) {
//结点为空则返回空if (root==null){return null;}
//结点左右子树都为空返回该结点if (root.left==null&&root.right==null){return root;}
//有一颗子树不为空则创建变量tmp交换两个结点TreeNode tmp=root.left;root.left=root.right;root.right=tmp;
//遍历左子树invertTree(root.left);
//遍历右子树invertTree(root.right);
//最后返回结点return root;}