二叉树|701.二叉搜索树中的插入操作

本文主要是介绍二叉树|701.二叉搜索树中的插入操作，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

力扣题目链接

class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}if (root->val > val) root->left = insertIntoBST(root->left, val);if (root->val < val) root->right = insertIntoBST(root->right, val);return root;}
};

不要被题目迷惑了，这题真的是个简单题啊！
哪里有空位插入哪里就好了！

代码随想录 (programmercarl.com)

思路

这道题目其实是一道简单题目，但是题目中的提示：有多种有效的插入方式，还可以重构二叉搜索树，一下子吓退了不少人，瞬间感觉题目复杂了很多。

其实可以不考虑题目中提示所说的改变树的结构的插入方式。

如下演示视频中可以看出：只要按照二叉搜索树的规则去遍历，遇到空节点就插入节点就可以了。

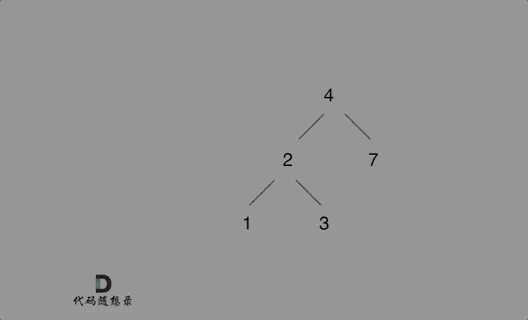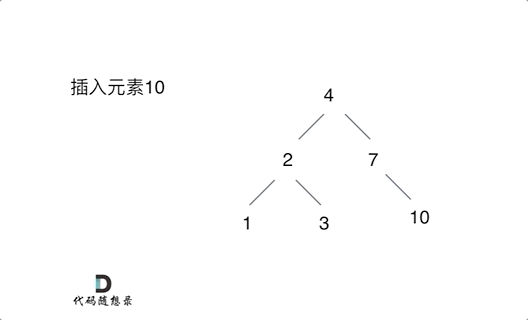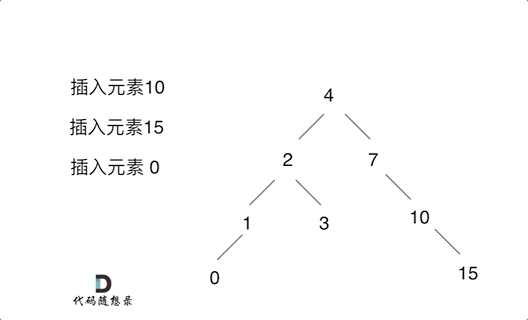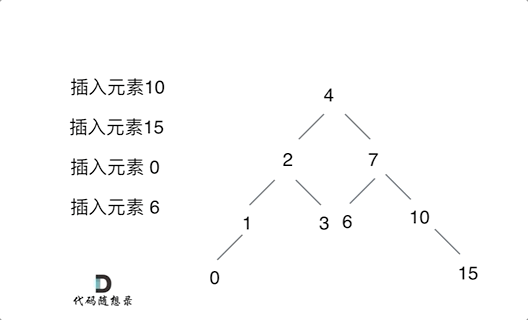
701.二叉搜索树中的插入操作

例如插入元素10 ，需要找到末尾节点插入便可，一样的道理来插入元素15，插入元素0，插入元素6，需要调整二叉树的结构么？并不需要。。

只要遍历二叉搜索树，找到空节点插入元素就可以了，那么这道题其实就简单了。

接下来就是遍历二叉搜索树的过程了。

#递归

递归三部曲：

确定递归函数参数以及返回值

参数就是根节点指针，以及要插入元素，这里递归函数要不要有返回值呢？

可以有，也可以没有，但递归函数如果没有返回值的话，实现是比较麻烦的，下面也会给出其具体实现代码。

有返回值的话，可以利用返回值完成新加入的节点与其父节点的赋值操作。（下面会进一步解释）

递归函数的返回类型为节点类型TreeNode * 。

代码如下：

TreeNode* insertIntoBST(TreeNode* root, int val)

确定终止条件

终止条件就是找到遍历的节点为null的时候，就是要插入节点的位置了，并把插入的节点返回。

代码如下：

if (root == NULL) {TreeNode* node = new TreeNode(val);return node;
}

这里把添加的节点返回给上一层，就完成了父子节点的赋值操作了，详细再往下看。

确定单层递归的逻辑

此时要明确，需要遍历整棵树么？

别忘了这是搜索树，遍历整棵搜索树简直是对搜索树的侮辱。

搜索树是有方向了，可以根据插入元素的数值，决定递归方向。

代码如下：

if (root->val > val) root->left = insertIntoBST(root->left, val);
if (root->val < val) root->right = insertIntoBST(root->right, val);
return root;

到这里，大家应该能感受到，如何通过递归函数返回值完成了新加入节点的父子关系赋值操作了，下一层将加入节点返回，本层用root->left或者root->right将其接住。

整体代码如下：

class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}if (root->val > val) root->left = insertIntoBST(root->left, val);if (root->val < val) root->right = insertIntoBST(root->right, val);return root;}
};

可以看出代码并不复杂。

刚刚说了递归函数不用返回值也可以，找到插入的节点位置，直接让其父节点指向插入节点，结束递归，也是可以的。