[AcWing]861. 二分图的最大匹配（C++实现）匈牙利算法匹配二分图模板题

1. 题目

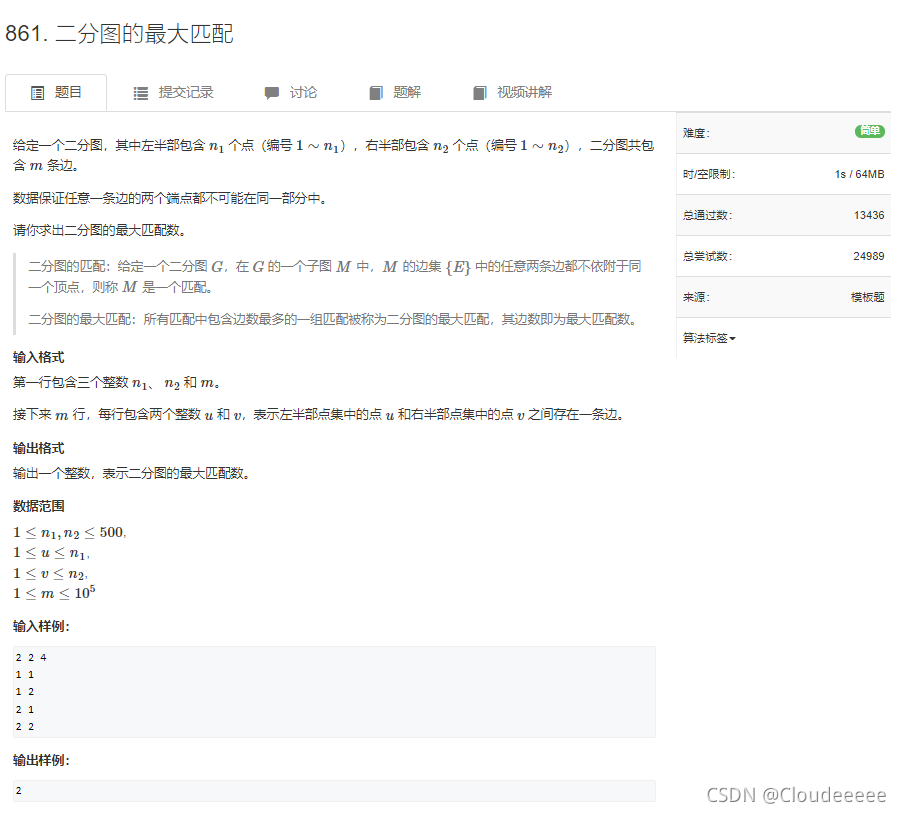
2. 读题（需要重点注意的东西）

思路：
首先要知道，什么是二分图。

二分图的定义如下： 二分图又称作二部图，是图论中的一种特殊模型。
设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i
in A,j in B)，则称图G为一个二分图。
简而言之：如果把无向图中的节点划分为两个互不相交的子集，图中一条边的两个端点分别属于这两个集合，这样的图就叫二分图。

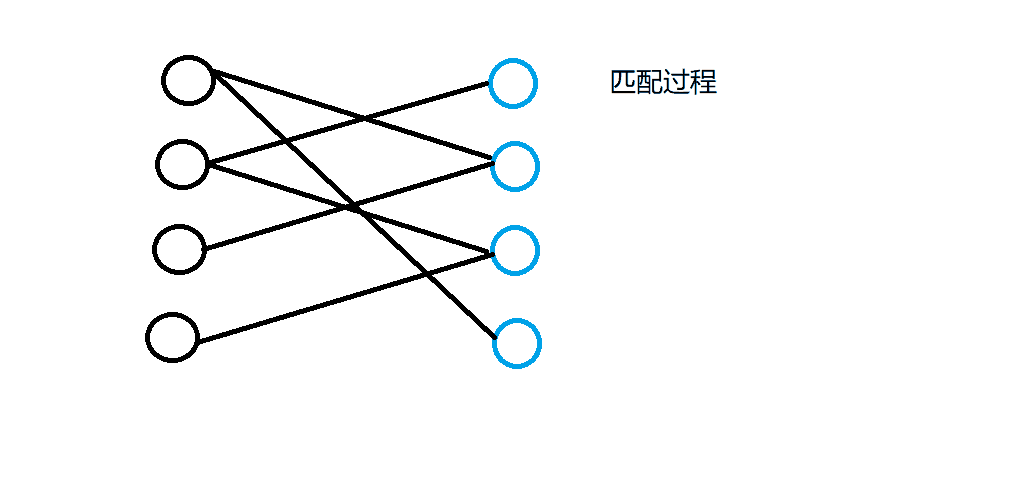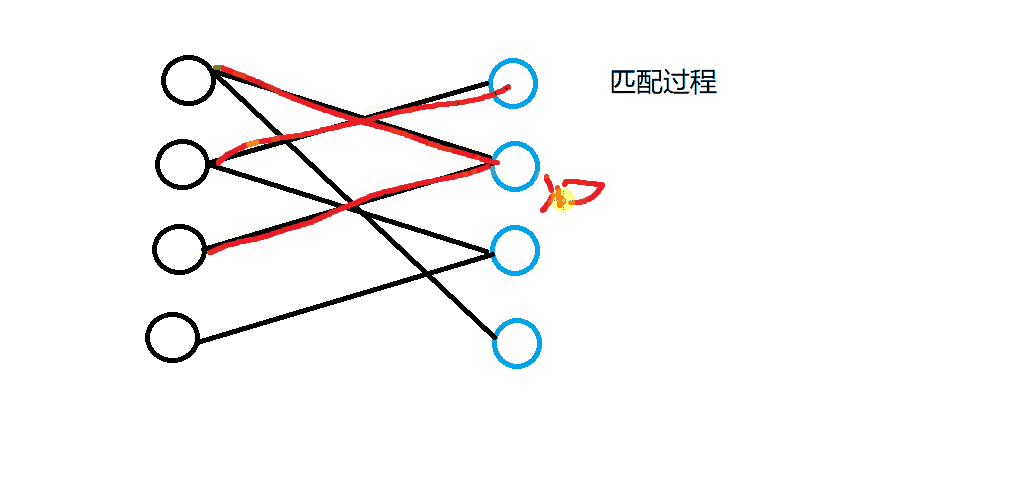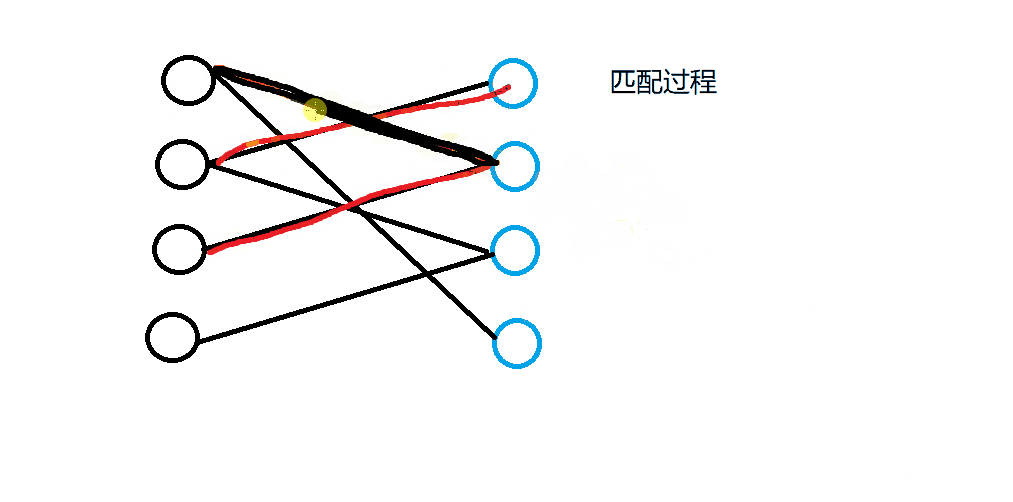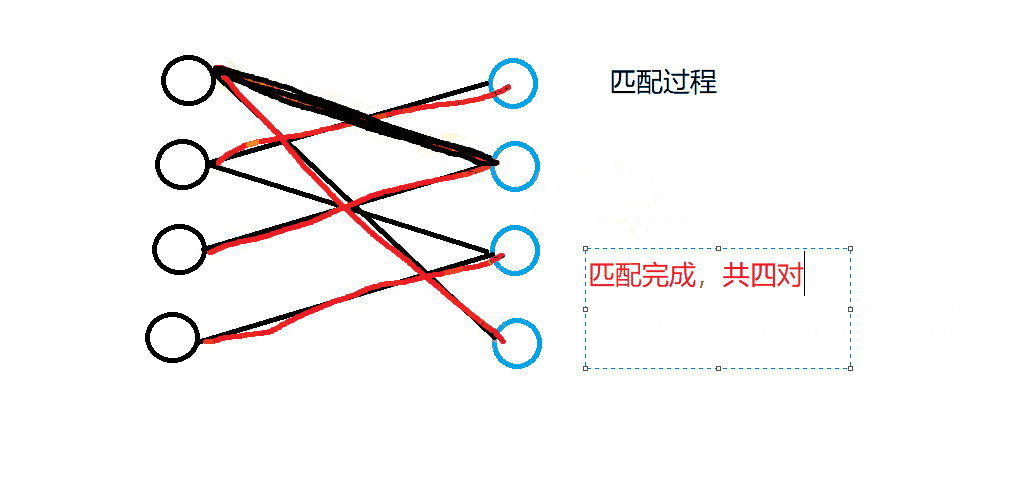
匈牙利算法匹配的主要思想是：
当发生匹配冲突时，看能否解决冲突，能的话就返回true，皆大欢喜；否则就返回false。匹配算法的流程如下图所示：

3. 解法

---------------------------------------------------解法---------------------------------------------------

#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 100010;int n1, n2, m;
int h[N], e[M], ne[M], idx; // 稀疏图用邻接表存储
int match[N];
bool st[N]; // st数组判重，即不要重复搜一个点void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}// 找给出的节点x能否配对
bool find(int x){for(int i = h[x];i != -1;i = ne[i]){int j = e[i]; // j是n2集合的一个数if(st[j] == 0){ // 如果j没考虑过，考虑它st[j] = 1; // j考虑过了，不重复考虑if(match[j] == 0 || find(match[j])){ // 如果j未配对，或者与j配对的值（在n1集合中）能再找一个值配对match[j] = x; // 则这个j与x配对return true; // 成功配对一组}}}return false;
}int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h, -1, sizeof h);while (m -- ){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for (int i = 1; i <= n1; i ++ ){memset(st, false, sizeof st); // 每次都要将st数组置位0，表示没有考虑过所有的节点if (find(i)) res ++ ; // 如果能成功配对，res加1表示成功配对的组数加1}printf("%d\n", res);return 0;
}

4. 可能有帮助的前置习题

5. 所用到的数据结构与算法思想

• 邻接表存储稀疏图

6. 总结

匈牙利算法计算二分图的最大匹配的模板题，背下来！