本文主要是介绍数学建模体育建模和经济建模国防科大版,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

目录
6.体育中的数学建模
7.经济学问题中的数学建模
7.1.实物交换模型
7.2.边际效应
7.3.最佳消费选择模型
6.体育中的数学建模
体育科学的研究中,也有大量的数学建模问题,例如:棒球的最佳击球点问题、滑板滑雪赛道的设计、越野自行车比赛车轮的选择、NBA赛程的科学性评价、划艇比赛中运动员的体力分配、体操团体赛出场队员的最佳组合等等。
越野长跑团体赛竞赛规则的公平性
越野长跑团体赛的竞赛规则如下:
越野长跑每个参赛团体由7名队员组成,取该团体跑在前面的5名队员在所有参赛选手中的排名顺序之和为该团体的得分。
然后根据各参赛队得分(由小到大)的顺序决定比赛排名。试讨论该竞赛规则的合理性并提出改进方案。
准则一:
二元独立性(binary independence在)A与B两个队的相对顺序不应当依赖于任何其他队的表现。
准则二:
孔多塞准则(Condorcet Criterion)一个队如果在与任一个队的两两对决中获胜,则这个队应当是整个比赛的优胜者。
准则三:
单调性准则(Monotonicity criterion)
如果A队是一次竞赛的获胜者。假设在另一次竞赛中所有的参赛队与选手都不 变,A队的一个选手a提高了名次,而其他所有参赛选手之间的相对顺序都不变,则A队仍应是获胜者。
准则四:
帕雷托条件(Pareto condition)如果A、B两队各有m个队员参赛,且有ai < bi:(i=1,2,…,m),则A队排名应优于B队。
(5,2)规则 一共7人参加,只取每队前5人成绩有效,其余2人成绩不计入
(5,2)规则的公平性判断
称现有规则为(5,2)规则,我们按照上述准则来判断该规则的公平性。
满足单调性和帕雷托条件
其他几种竞赛规则评价
名次加权(m,l)规则 名次差异非均匀化。
名次加权(m,l)规则不满足二元独立性与孔多塞准则,但满足单调性与帕雷托条件。
迭代(m,0)规则 每次淘汰最后一名,然后重新计算名次。
顺序孔多赛规则 按任意顺序,前两队对决,胜者与下一队对决,如此进行下去,最后留下的队就是获胜队。
非团体规则 存在i,使得 ai<bi A<B
越野团体赛计分规则的阿罗定理
以名次为排序依据,那么,在有至少三个队参加的越野团体赛中,如果一个规 则同时满足二元独立性与帕雷托条件,则该规则是非团体规则。
合理计分规则:
采用(m,l)竞赛方案,记录所有运动员比赛时间,按照国际田联《田径 项目分值表》转换为得分,取各队前m名队员的总得分为排序依据。
时间排序规则
按各队前5名队员的竞赛时间之和排名。
满足四条准则
准则5:
成绩与训练难度匹配原则
一个团队的成绩,应体现获得该成绩所需要的训练难度。
7.经济学问题中的数学建模
“边际效用”是经济学中十分重要的概念,本讲通过实物交换模型、最佳消费选择模型、报童售报问题等建模案例,了解边际效用概念在生活、生产实际中的应用。
-
边际效用
-
边际收入
-
边际成本
7.1.实物交换模型
实物交换的原则是:互通有无,等价交换
设交换前甲有物品X的数量为x0,乙有物品Y的数量为y0,交换后甲有物品X和Y的数量分别为x和y。
也叫满意度曲线
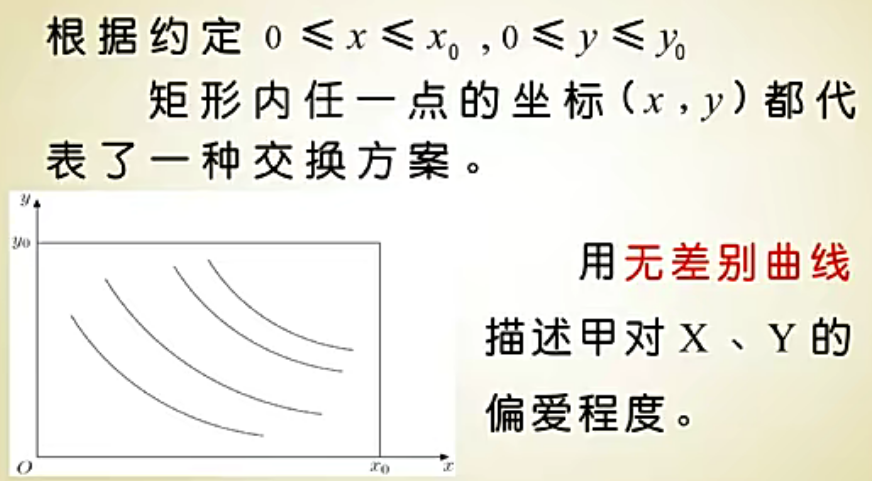
于是矩形0≤x≤x0,0≤y≤y0以内任一点的坐标(x,y)都代表了一种交换方案。
用无差别曲线描述甲对X、Y的偏爱程度
甲有无数条无差别曲线,记为f(x, y) = C1
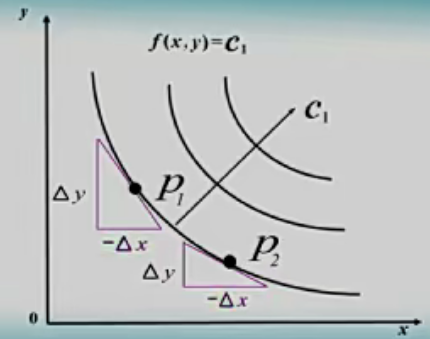
无差别曲线应满足
-
单调减的:物品X的增加必须以物品Y的减少为代价。
-
互不相交的:对同一交换方案不应有不同的满意度值。

7.2.边际效应
我们向往某事物时,情绪投入越多,第一次接触到此事物时情感体验也越为强烈,但是,第二次接触时,会淡一些,第三次,会更淡……以此发展,我们接触该事物的次数越多,我们的情感体验也越为淡漠,一步步趋向乏味。这种效应,在经济学和社会学中同样有效,在经济学中叫“边际效益递减率”,在社会学中叫“剥夺与满足命题”,是由霍曼斯提出来的,用标准的学术语言说就是:“某人在近期内重复获得相同报酬的次数越多,那么,这一报酬的追加部分对他的价值就越小。”
效用是一种主观偏好,个人的目标是效用最大化。
设某人关于商品X与Y的效用函数U=U(x, y),则该人消费最后一单位商品所得到的效用(边际效用Marginal Utility)分别为 αU / αx αU / αy
例(面包与苹果)
一个面包价值2元,一个苹果价值1元,张三已有2个面包与2个苹果,假设这时面包的边际效用为3个单位,苹果的边际效用是1个单位,张三接下来会购买哪一种商品?
解:
3/2=1.5,1/1=1。即张三接下来花一元钱购买苹果可带来1个单位的效 用增量,而购买面包可带来1.5个单位的效用增量。
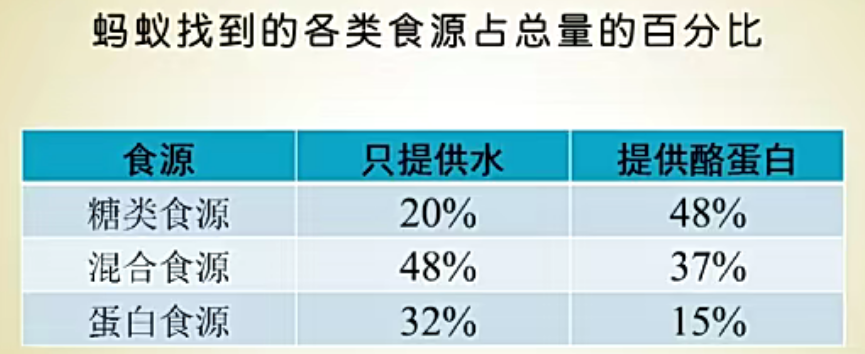
例(蚂蚁的选择)
生物学家Adam Kay研究了蚂蚁的觅食选择。实验中,每天给蚁群一定量的6% 浓度的酪蛋白溶液,观察是否会影响它们在蛋白质食源和糖类食源之间的选择。控制组的蚁群待遇一样,只是用清水代替了酪蛋白溶液。
在市场竞争条件下,边际收入是产量的递减函数,而边际成本是产量的递增函数。
7.3.最佳消费选择模型
问题:
在资金一定条件下,如何求最佳的商品消费比例。
边际效用递减规律:
边际效用随着消费增加而下降。
最后一元钱的边际效用:

边际分析
-
边际收入
-
边际成本
-
边际效用
利润最大化原理
在连续情形下当边际收入等于边际成本即dR/dQ=dC/dQ时达到最优产量。
边际利润=边际收入一边际成本
令上述为0得
若设每天报纸的需求份数为X,则:P(X=n)(a-b)=P(X<n)(b-c)


这篇关于数学建模体育建模和经济建模国防科大版的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








