LeetCode 热题 HOT 100(P21~P30)

 public void rotate(int[][] matrix) {final int row = matrix.length;final int col = matrix[0].length;//上下翻转for (int i = 0; i < row / 2; i++) {for (int j = 0; j < col; j++) {swap(matrix, i, j, row - i - 1, j);}}//对角线翻转for (int i = 0; i < row; i++) {for (int j = i + 1; j < col; j++) {swap(matrix, i, j, j, i);}}}private void swap(int[][] matrix, int rowIndex, int colIndex, int newRowIndex, int newColIndex) {int tmp = matrix[rowIndex][colIndex];matrix[rowIndex][colIndex] = matrix[newRowIndex][newColIndex];matrix[newRowIndex][newColIndex] = tmp;}

LC49group_anagrams

. - 力扣（LeetCode）

题目：

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

解法：

理解题目的意思有点费劲，实际就是由相同字母组成单词的集合，很自然的想到用HashMap 。

 public List<List<String>> groupAnagrams(String[] strs) {Map<String, List<String>> cache = new HashMap<>();for (String str : strs) {final char[] chars = str.toCharArray();Arrays.sort(chars);cache.computeIfAbsent(new String(chars), (k) -> new ArrayList<String>()).add(str);}return new ArrayList<>(cache.values());}

写出代码不难，关键是能否写的尽量简练。

LC53maximum_subarray

. - 力扣（LeetCode）

题目：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

解法：

一般这种最*** 的题目理论上都可以用动态规划，核心难点是动态数组的定义，很多时候动态数组定义好了，动态推导方程也能比较简单的推演出来。

动态数组：dp[i] 表示包含下标i的连续子数组最大和

动态方程：dp[i] = Max(i,dp[i-1]+i) 

比较好理解的，这里稍微解释下包含i的数组最大和，基本要看前一位最大和是否小于0，如果是负数带上前面的肯定更小，还不如自己玩（i），如果前面大于0，那么带上肯定更大。

public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int max = dp[0];for (int i = 1; i < nums.length; i++) {dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);max = Math.max(max, dp[i]);}return max;}

因为i只跟i-1 有关，因此动态数组可以简化为单个变量，其实动态规划很多代码都可以简化为单个或多个变量，但是这样的话代码就不太好理解。

LC55jump_game

. - 力扣（LeetCode）

题目：

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

解法：

可能也算套路题，有思路之后很简单。其实就是每跳一步就记录当前能跳到的最远位置，然后一个个位置跳过去，判断当前记录最远位置能否到下一个。实际上也是动态规划的思路。

动态数组：dp[i] 表示在i位置时能跳到的最远下标

动态方程：dp[i] = max(dp[i-1],i+nums[i])

 public boolean canJump(int[] nums) {//表示能达到的最远距离int k = 0;for (int i = 0; i < nums.length; i++) {if (k < i) {return false;}k = Math.max(k, i + nums[i]);}//能抵达最后一块石头就okreturn true;}

这里将动态数组精简为单个变量。

LC56merge_intervals

. - 力扣（LeetCode）

题目：

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

解法：

区间合并的问题，首先是排序，按照starti 排序。然后就是进行入队操作，在入队的时候跟队首元素进行比较，看下当前元素starti 是否大于队首元素的endi，如果大于说明需要开一个新的区间，如果小于那就加入当前区间。

public int[][] merge(int[][] intervals) {// 先按照区间起始位置排序Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);// 遍历区间List<int[]> result = new ArrayList<>();for (int[] interval : intervals) {// 如果结果数组是空的，或者当前区间的起始位置 > 结果数组中最后区间的终止位置，// 则不合并，直接将当前区间加入结果数组。if (result.isEmpty() || interval[0] > result.get(result.size() - 1)[1]) {result.add(interval);} else {final int[] ints = result.get(result.size() - 1);ints[1] = Math.max(ints[1], interval[1]);}}return result.toArray(new int[0][]);}

注意合并的写法，需要取当前元素的endi 和队首元素的endi 的最大值，在这里踩过坑。

LC62unique_paths

. - 力扣（LeetCode）

题目：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

解法：

因为每次只能向下或者向右移动一步，因此要走到右下角，上一步只能从下面下来，或者从左边过来。对每个位置来说也可以这么推断，这里动态数组定义比较直观dp[i,j] 就是走到坐标[i,j] 一共有多少路径。动态方程dp[i,j] = dp[i-1,j] + dp[i,j-1]  。这里还涉及到动态数组的初始化，第一列和第一排的走法只有1种。

 public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];//初始化行列的情况for (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int i = 0; i < n; i++) {dp[0][i] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}

LC64minimum_path

. - 力扣（LeetCode）

题目：

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

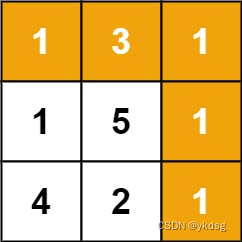
解法：

这道题跟上一道类似，不同的是这里求最小和，其实走法是一样的，因为只能从上面或者左边过来。动态数组定义为当前位置的最小值，动态方程有所调整，dp[i,j]=min(dp[i-1,j],dp[j,i-1]) +nums[i,j] 。 

 public int minPathSum(int[][] grid) {final int m = grid.length, n = grid[0].length;int[][] dp = new int[m][n];dp[0][0] = grid[0][0];for (int i = 1; i < m; i++) {dp[i][0] = grid[i][0] + dp[i - 1][0];}for (int i = 1; i < n; i++) {dp[0][i] = grid[0][i] + dp[0][i - 1];}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1];}

这里有个优化，可以不用新增动态数组dp ，直接在原数组grid 上直接操作，这样能节省内存开销。

LC70climbing_stairs

. - 力扣（LeetCode）

题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

解法：

经典的爬楼梯算法题，他可以用递归的方式，也可以使用动态规划的思路。这类题目乍一看没思路，实际跟上面机器人走路是一样，要么从前1个台阶过来，要么从前2个台阶过来。动态方程比较简单：dp[i] = dp[i-1]+dp[i-2] 。因为只涉及前2个值，可以用2个变量替代数组。

public int climbStairs(int n) {if (n < 3) {return n;}int one = 1;int two = 2;for (int i = 3; i <= n; i++) {int cur = one + two;one = two;two = cur;}return two;}

LC72edit_distance

. - 力扣（LeetCode）

题目：

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

解法：

差不多也是套路题，这道题目跟机器走路的思路类似，可以参考下面的图

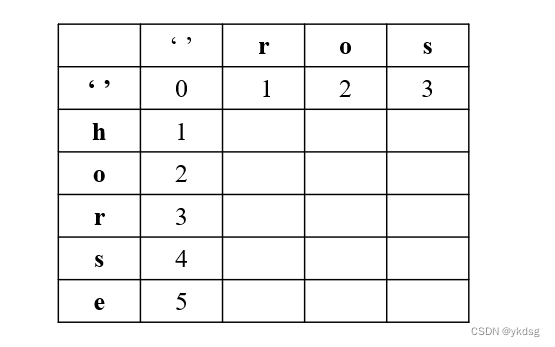
dp[i][j] 表示wrod1 的前 i 个字符转换成word2 的前j个字段所用的最小操作数 。相当于求最后一个格子的值。有点复杂的地方在于第一行和第一列作为空串进行初始化，第一行的意思是空串 ‘’ 变成'ros'  所需的最小步骤。第一列同理，这样就初始化好了动态数组。这里的动态方程有点复杂，需要分情况判断：

• 当 word1[i] == word2[j]，dp[i][j] = dp[i-1][j-1]；
• 当 word1[i] != word2[j]，dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1 ；
  • dp[i-1][j-1] 表示替换操作
  • dp[i-1][j] 表示删除操作
  • dp[i][j-1] 表示插入操作。

public int minDistance(String word1, String word2) {final int row = word1.length();final int col = word2.length();// 因为有初始行和初始列，所以这里长度+1int[][] dp = new int[row + 1][col + 1];for (int i = 0; i <= row; i++) {dp[i][0] = i;}for (int i = 0; i <= col; i++) {dp[0][i] = i;}for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (word1.charAt(i) == word2.charAt(j)) {dp[i + 1][j + 1] = dp[i][j];} else {dp[i + 1][j + 1] = Math.min(Math.min(dp[i][j], dp[i][j + 1]), dp[i + 1][j]) + 1;}}}return dp[row][col];}

LC75sort_colors

. - 力扣（LeetCode）

题目：

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

解法：

套路题，需要了解思路。维护0，1，2的初始下标，其中0，1初始在0，2初始在len-1，然后迭代数组，对数组中的数字进行判断，并相应的移动下标。可以参考官方的讲解配图，比较好理解。

public void sortColors(int[] nums) {if (nums.length == 0) {return;}//定义几个下标，需要实现// all in [0, zero] = 0// all in (zero, i) = 1// all in (two, len - 1] = 2int zero = 0, cur = 0, two = nums.length - 1;while (cur <= two) {if (nums[cur] == 0) {swap(nums, zero, cur);zero++;cur++;} else if (nums[cur] == 1) {cur++;} else {swap(nums, cur, two);//注意 这个时候cur 不能移动，因为交换之后还要再判断下two--;}}}private void swap(int[] nums, int i, int j) {final int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}