[NOI2005]月下柠檬树[计算几何（simpson）]

本文主要是介绍[NOI2005]月下柠檬树[计算几何（simpson）]，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1502: [NOI2005]月下柠檬树

Time Limit: 5 Sec Memory Limit: 64 MB
Submit: 1169 Solved: 626
[Submit][Status][Discuss]

Description

Input

文件的第1行包含一个整数n和一个实数alpha，表示柠檬树的层数和月亮的光线与地面夹角(单位为弧度)。第2行包含n+1个实数h0,h1,h2,…,hn，表示树离地的高度和每层的高度。第3行包含n个实数r1,r2,…,rn，表示柠檬树每层下底面的圆的半径。上述输入文件中的数据，同一行相邻的两个数之间用一个空格分隔。输入的所有实数的小数点后可能包含1至10位有效数字。

Output

输出1个实数，表示树影的面积。四舍五入保留两位小数。

Sample Input

2 0.7853981633
10.0 10.00 10.00
4.00 5.00

Sample Output

171.97

HINT

1≤n≤500，0.3

Source

求一棵树(圆锥加圆台组成)在平面上的投影的面积。

给定投影角度(0.3 < alpha <= pi/2)。

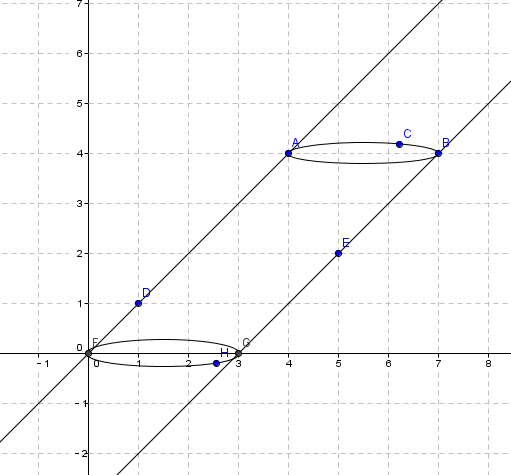
先来想想圆的投影是什么样子

这里写图片描述

还是他自己。

再想圆锥投影是什么样子

一个点加一个圆，并且有这个点与该圆的两条切线(该点在圆内部时没有切线)

再想圆台

两个圆，加上两个圆的外公切线组成的一坨图形。

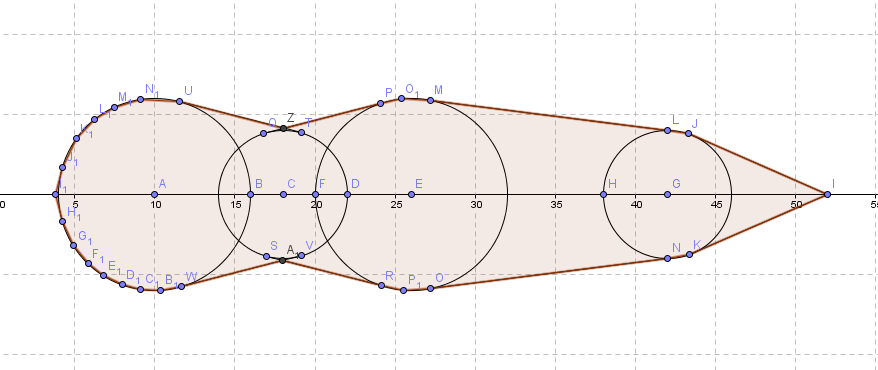
不妨随意画一个。

这里写图片描述

好难画- -!

大概就转化成这个样子了。

观察这个图形…

轴对称啊- -!

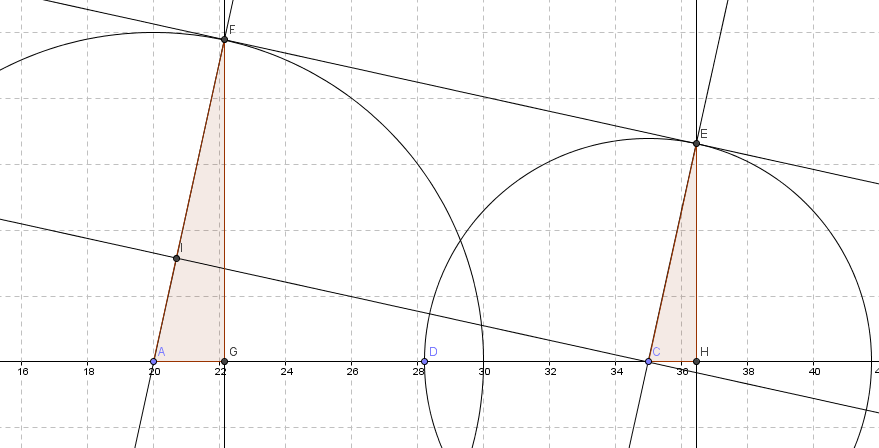
这里写图片描述

首先AC长是圆心距，可求。

AI长是半径差，可求。

所以CI可求。

连接FC，观察△FAC

2S△FAC=FGAC=CI*AF

AF为半径，已知。

所以FG可求。

于是AG可求。

A点坐标已知，所以F点坐标已知。

E点，直接相似即可。

或者用射影定理求EF

概述图中，在Rt△ABC中，∠ABC=90°，BD是斜边AC上的高，则有射影定理如下：

BD²=AD·CD

AB²=AC·AD

BC²=CD·AC

#include<cmath>
#include<cstdio>
#include<algorithm>
#define pf(x) ((x)*(x))
using namespace std;
const int N=2000+5;
const double eps=1e-6;
typedef pair<double,double> point;
typedef pair<double,double> circle;
struct line{point s,t;double k,b;line(){}line(point _s,point _t){s=_s;t=_t;k=(s.second-t.second)/(s.first-t.first);b=s.second-s.first*k;}const double f(const double x){return k*x+b;}
};
int n,n1;double alpha,H[N];
point p;line L[N];circle C[N];
double lb=2e9,rb;
double sina,cosa,tana;
inline void add(const circle &a,const circle &b){n1++;sina=(a.second-b.second)/(b.first-a.first);cosa=sqrt(1-pf(sina));tana=sina/cosa;L[n1].s=make_pair(a.first+a.second*sina,a.second*cosa);L[n1].t=make_pair(b.first+b.second*sina,b.second*cosa);L[n1].k=-tana;L[n1].b=L[n1].s.second-L[n1].s.first*L[n1].k;
}
inline const double F(const double x){double re=0;for(int i=1;i<=n1;i++) if(x>=L[i].s.first&&x<=L[i].t.first) re=max(re,L[i].f(x));for(int i=1;i<=n;i++) if(x>=C[i].first-C[i].second&&x<=C[i].first+C[i].second) re=max(re,sqrt(pf(C[i].second)-pf(x-C[i].first)));return re;
}
inline const double simpson(const double l,const double r){double mid=(l+r)/2;return (F(l)+F(r)+4*F(mid))*(r-l)/6;
}
inline double asr(double l,double r,double eps,double last){double mid=(l+r)/2;double L=simpson(l,mid),R=simpson(mid,r);if(fabs(L+R-last)<=15*eps) return L+R+(L+R-last)/15;return asr(l,mid,eps/2,L)+asr(mid,r,eps/2,R);
}
inline int cmp(const double x){if(fabs(x)<eps) return 0;return x>0?1:-1;
}
int main(){scanf("%d%lf",&n,&alpha);for(int i=1;i<=n+1;i++) scanf("%lf",&H[i]),H[i]+=H[i-1];for(int i=1;i<=n;i++) scanf("%lf",&C[i].second);double ta=tan(alpha);p=make_pair(H[n+1]/ta,0);rb=max(rb,p.first);double x,r,l,h;C[n].first=H[n]/ta;x=C[n].first;r=C[n].second;lb=min(lb,x-r);rb=max(rb,x+r);if(x+r<p.first){l=pf(r)/(p.first-x);// 射影定理 h=sqrt(pf(r)-pf(l));L[++n1]=line(make_pair(x+l,h),p);}for(int i=n-1;i;i--){C[i].first=H[i]/ta;x=C[i].first;r=C[i].second;lb=min(lb,x-r);rb=max(rb,x+r);if(cmp(C[i+1].first-x-fabs(C[i+1].second-r))>0)//内含 add(C[i],C[i+1]);}printf("%.2lf\n",2*asr(lb,rb,eps,simpson(lb,rb)));return 0;
}