c++曲线拟合：贝塞尔曲线的控制点计算

废话不说，直接上代码（后面示例点对应的绘制效果）：

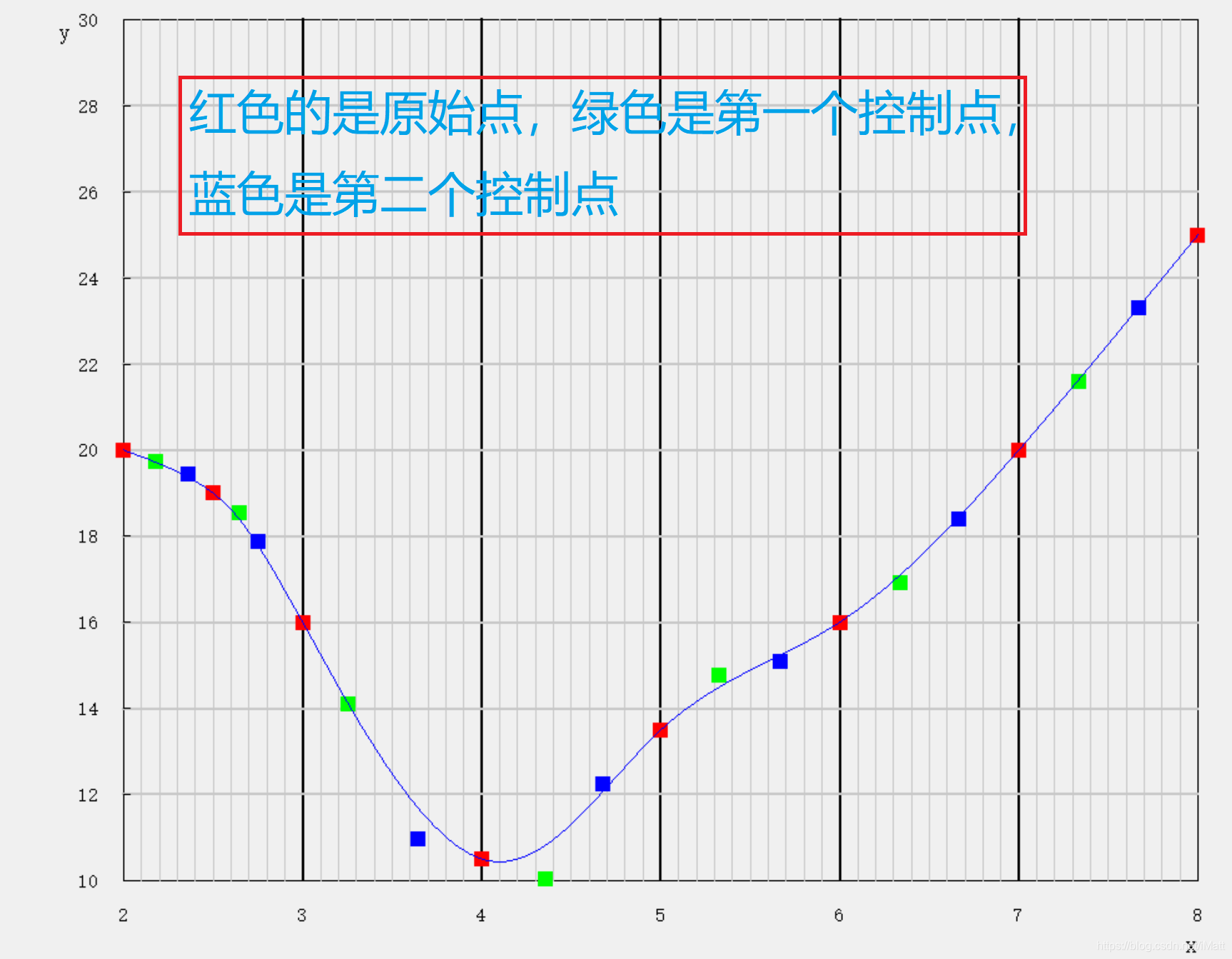
不计算控制点的原始折线：

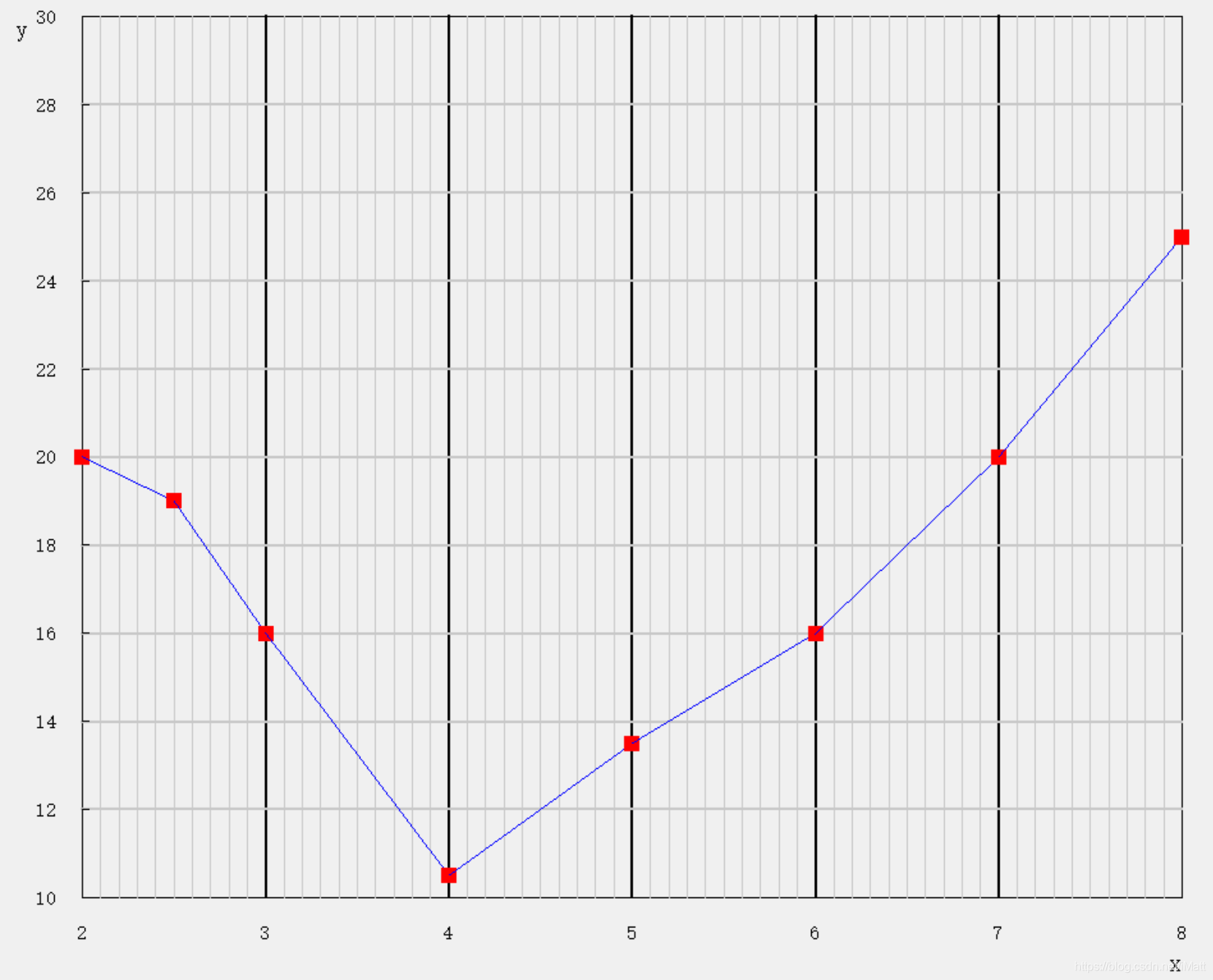
优化了代码的实现，使用STL代码更简洁

/*** @brief CalculateControlPoint 计算三次贝塞尔的控制点。* 三次方贝塞尔曲线由四个点定义: 起点、终点 和两个控制点。* @param rawPointVector [in]原始点数组* @param firstControlPointVector  [out]第一个控制点,总是比原始点数目少1，和第二个控制点数目相同* @param secondControlPointVector [out]第二个控制点，总是比原始点数目少1，和第一个控制点个数相同* @return 执行成功返回true,否则返回false。原始点数目必须不少于2，否则失败* @note 贝塞尔曲线得到之后，使用如下:*          原始点[0],*              第一个控制点[0],第二个控制点[0],原始点[1],*              第一个控制点[1],第二个控制点[1],原始点[2],*              第一个控制点[2],第二个控制点[2],原始点[3],*                  .*                  .*                  .*              第一个控制点[n-1],第二个控制点[n-1],原始点[n],*/
bool CalculateControlPoint(const std::vector<Point2D>& rawPointVector,std::vector<Point2D>& firstControlPointVector,std::vector<Point2D>& secondControlPointVector )
{if ( rawPointVector.size( ) < 2 ){printf("输入点至少是2个\n");return false;}std::size_t nPointSize = rawPointVector.size( ) - 1;const Point2D* pRawPoint = rawPointVector.data();if ( 1 == nPointSize ){// 特殊情况: 贝塞尔曲线是直线.// 3P1 = 2P0 + P3firstControlPointVector.resize(1);firstControlPointVector[0].X =(2 * pRawPoint[0].X + pRawPoint[1].X) / 3;firstControlPointVector[0].Y = (2 * pRawPoint[0].Y + pRawPoint[1].Y) / 3;// P2 = 2P1 – P0secondControlPointVector.resize(1);secondControlPointVector[0].X = 2 * firstControlPointVector[0].X - pRawPoint[0].X;secondControlPointVector[0].Y =	2 * firstControlPointVector[0].Y - pRawPoint[0].Y;return true;}std::vector<double> rhs(nPointSize);double* pTmp = rhs.data();for (std::size_t i = 1; i < nPointSize - 1; ++i){pTmp[i] = 4 * pRawPoint[i].X + 2 * pRawPoint[i + 1].X;}pTmp[0] = pRawPoint[0].X + 2 * pRawPoint[1].X;pTmp[nPointSize - 1] = (8 * pRawPoint[nPointSize - 1].X + pRawPoint[nPointSize].X) / 2.0;std::vector<double> x;GetFirstControlPoints(rhs,x);for (std::size_t i = 1; i < nPointSize - 1; ++i)pTmp[i] = 4 * pRawPoint[i].Y + 2 * pRawPoint[i + 1].Y;pTmp[0] = pRawPoint[0].Y + 2 * pRawPoint[1].Y;pTmp[nPointSize - 1] = (8 * pRawPoint[nPointSize - 1].Y + pRawPoint[nPointSize].Y) / 2.0;std::vector<double> y;GetFirstControlPoints(rhs,y);double* pX = x.data();double* pY = y.data();firstControlPointVector.resize( nPointSize );secondControlPointVector.resize( nPointSize );Point2D* pFirstPoints = firstControlPointVector.data();Point2D* pSecondPoints = secondControlPointVector.data();for (std::size_t i = 0; i < nPointSize; ++i){// Second control pointpFirstPoints[i].X = x[i];pFirstPoints[i].Y = y[i];if (i < nPointSize - 1){pSecondPoints[i].X = 2 * pRawPoint[i + 1].X - pX[i + 1];pSecondPoints[i].Y = 2 * pRawPoint[i + 1].Y - pY[i + 1];}else{pSecondPoints[i].X = (pRawPoint[nPointSize].X + pX[nPointSize - 1]) / 2;pSecondPoints[i].Y = (pRawPoint[nPointSize].Y + pY[nPointSize - 1]) / 2;}}return true;
}

用到的其它函数：

#include <math.h>
#include <vector>
typedef struct tagPoint2D
{inline tagPoint2D( double x=0.0, double y=0.0):X(x),Y(y){}double X;double Y;
}Point2D;static std::vector<double> GetFirstControlPoints(const std::vector<double>& rhs, std::vector<double>& x )
{std::size_t n = rhs.size( );x.resize( n );std::vector<double> tmp( n );double b = 2.0;x[0] = rhs[0] / b;for (std::size_t i = 1; i < n; ++i ) // Decomposition and forward substitution.{tmp[i] = 1 / b;b = (i < n - 1 ? 4.0 : 3.5) - tmp[i];x[i] = (rhs[i] - x[i - 1]) / b;}for (std::size_t i = 1; i < n; ++i )x[n - i - 1] -= tmp[n - i] * x[n - i]; // Backsubstitution.return x;
}

使用样例：

    std::vector<BezierSplie::Point2D> rawPointVector;rawPointVector.push_back( BezierSplie::Point2D(2.0f,20.0f) );rawPointVector.push_back( BezierSplie::Point2D(2.5f,19.0f) );rawPointVector.push_back( BezierSplie::Point2D(3.0f,16.0f) );rawPointVector.push_back( BezierSplie::Point2D(4.0f,10.5f) );rawPointVector.push_back( BezierSplie::Point2D(5.0f,13.5f) );rawPointVector.push_back( BezierSplie::Point2D(6.0f,16.0f) );rawPointVector.push_back( BezierSplie::Point2D(7.0f,20.0f) );rawPointVector.push_back( BezierSplie::Point2D(8.0f,25.0f) );std::vector<BezierSplie::Point2D> firstPointVector;std::vector<BezierSplie::Point2D> secondPointVector;BezierSplie::CalculateControlPoint( rawPointVector,firstPointVector,secondPointVector );printf("\nfirst control point:\n");for( auto it = firstPointVector.begin(); it != firstPointVector.end(); ++it ){printf("(%f,%f);", it ->X, it ->Y );}printf( "\nsecond second point: \n");for( auto it = secondPointVector.begin(); it != secondPointVector.end(); ++it ){printf("(%f,%f);", it ->X, it ->Y );}

计算原理：

先来看2个点的贝塞尔：

B(t)=(1−t)3P0+3(1−t)2tPc0+3(1−t)t2Pc1+t3P1 (1)

B′(t)=−3(1−t)2P0+3(3t2−4t+1)Pc0+3(2t−3t2)Pc1+3t2P1 (2)

B′′(t)=6(1−t)P0+3(6t−4)P1+3(2−6t)P2+6tP3 (3)

2个控制点为直线，那么（1）式中的2次和3次项为0

得到：

3Pc1 = 2P0+P1 （*1）

Pc2  = 2Pc1–P0 （*2）

拓展到i阶的贝塞尔

Bi(t)=(1−t)3Pi−1+3(1−t)2tPci+3(1−t)t2Pci+1+t3Pi  (i=1,..,n) （4）

对应的1阶导:

B′i(t)=−3(1−t)2Pi−1+3(3t2−4t+1)Pci+3(2t−3t2)Pci+1+3t2Pi (i=1,..,n)（5）

一阶倒数连续的条件：B′i−1(1)=B′i(0)，得到：

Pci+Pc(i−1)+1=2Pi−1;…(i=2,..,n)  （6）

对应的2阶导：

B′′i(t)=6(1−t)Pi−1+6(3t−2)Pci+6(1−3t)Pci+1+6tPi (i=1,..,n) （7）

同样二阶导 B’’i-1(1)=B’’i(0) ，得到:

Pc(i−1)+Pci+1=Pci+1+2Pc(i−1)+1 (i=2,..,n) （8）

对贝塞尔所有点，总是有B’’1(0)=0和B’’i(n)=0（因为起始和终止点）

2Pc1−Pc1+1=P0 （9）

2Pcn+1−Pcn=Pn （10）

整合（6）（8）（9）（10）,对于第n个点控制点Pcn和Pcn+1,有：

2Pc1+Pc1+1=P0+2P1Pc1+4Pc1+1+Pc3=4P1+2P2 (11)

Pc(i−1)+4Pci+Pc(i+1)=4Pi−1+2Pi (12)

Pc(n−2)+4Pc(n−1)+Pcn=4Pn−2+2Pn−12Pc(n−1)+7Pcn=8Pn−1+Pn (13)

（12）是一般表达，如果知道第一个控制点，按照上面公式（6）（8）（9）（10）可以得到第二个控制点。

csdn不支持格式，WORD截图：