本文主要是介绍day34 第八章 贪心算法 part03● 1005.K次取反后最大化的数组和 ● 134. 加油站● 135. 分发糖果,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

自己写的情况理不清楚,wa了好几次才ac。
比如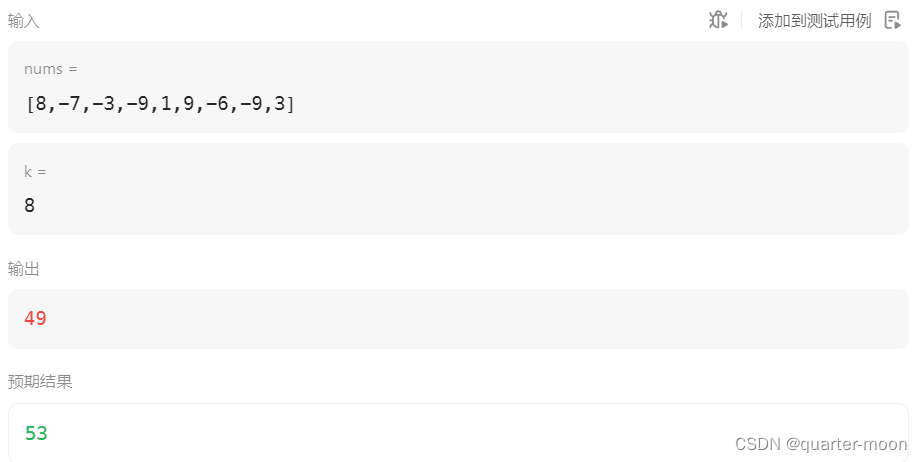
如果 k比负数多,且多的数是奇数3,那么最后变为符号的应该是绝对值最小的数,而不是负数中最大的数。
比如:

我只考虑了k的次数大于负数的数量,但是没考虑大于数组的整体长度。按照我原来代码,是直接遍历结束了,所有负数取反求和得到9。要特判,如果k比负数多出来数量是奇数,要处理,减去绝对值最小的数的两倍,因为之前加了两次。
class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {int ans=0;sort(nums.begin(),nums.end());int fu=0;int ci=0;int flag=1;int mi=101;for(int i=0;i<nums.size();i++){mi=min(mi,abs(nums[i]));if(flag==1&&nums[i]<=0){ci++;ans+=(-nums[i]);if(k==ci){flag=0;}}else{if(k>ci){if((k-ci)%2!=0) {if(i==0){ans-=(nums[i]); }else{if(nums[i]>-nums[i-1]){ans+=(nums[i-1])*2;ans+=nums[i];}else{ans-=nums[i];} }}else{ans+=nums[i];}ci=k;}else{ans+=nums[i];}}}if(k>ci&&((k-ci)%2!=0)){ans-=(2*mi);}return ans;}
};贪心的思路,局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
局部最优可以推出全局最优。
那么如果将负数都转变为正数了,K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
那么又是一个贪心:局部最优:只找数值最小的正整数进行反转,当前数值和可以达到最大(例如正整数数组{5, 3, 1},反转1 得到-1 比 反转5得到的-5 大多了),全局最优:整个 数组和 达到最大。题解的代码就归纳的比较整齐,因为直接按照绝对值排序。
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时K--
- 第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
- 第四步:求和
class Solution {
static bool cmp(int a, int b) {return abs(a) > abs(b);
}
public:int largestSumAfterKNegations(vector<int>& A, int K) {sort(A.begin(), A.end(), cmp); // 第一步for (int i = 0; i < A.size(); i++) { // 第二步if (A[i] < 0 && K > 0) {A[i] *= -1;K--;}}if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步int result = 0;for (int a : A) result += a; // 第四步return result;}
};
能想到的是
直接从全局进行贪心选择,情况如下:
-
情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
-
情况二:rest[i] = gas[i]-cost[i]为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
-
没想到(清)的是:比如如果累加有多个负数,该怎么填平。但其实只要考虑最小的负数就行,因为在填平最小的过程中就会填上次小的。
情况三:如果累加的最小值是负数,汽车就要从非0节点出发,从后向前,看哪个节点能把这个负数填平,能把这个负数填平的节点就是出发节点。
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int sum=0;int mi=INT_MAX ;for(int i=0;i<gas.size();i++){sum+=gas[i]-cost[i];if(sum<mi){mi=sum;}}if(sum<0) return -1;if(mi>=0) return 0;for(int i=gas.size()-1;i>=0;i--){int tmp=gas[i]-cost[i];mi=mi+tmp;if(mi>=0){return i;}}return -1;}};
感觉没法两边同时考虑。看了题解,但其实就是试试看的问题。
先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
局部最优可以推出全局最优。
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个,所以贪心:candyVec[i] = candyVec[i - 1] + 1
再确定左孩子大于右孩子的情况(从后向前遍历)
所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
class Solution {
public:int candy(vector<int>& ratings) {int sum=0;int len=ratings.size();vector<int> res(len+1,1);for(int i=1;i<len;i++){if(ratings[i]>ratings[i-1]){res[i]=res[i-1]+1;}}for(int i=len-2;i>=0;i--){if(ratings[i]>ratings[i+1]){res[i]=max(res[i],res[i+1]+1);}sum+=res[i];}sum+=res[len-1];return sum;}
};这篇关于day34 第八章 贪心算法 part03● 1005.K次取反后最大化的数组和 ● 134. 加油站● 135. 分发糖果的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




