本文主要是介绍编码:KR字符串匹配,一个简单到领导都看得懂的算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
“ 常怀感恩,生活或许就不会处处深渊。”
这几天看了《柔性字符串匹配》,觉得很有意思。书是好书,只是这个脑子是不是猪脑就不知道了,于是秉着知之为知之,不知为不知的精神,我准备再次去请教一下我的领导,在一个月黑风高的夜晚,我给领导发了个消息,领导这么回复了我。
01
—
**KR算法
**
话说回来,我们今天要说的这个字符串匹配算法比之前讲过的kmp,horspool,sunday简单的多的字符串匹配算法,我们知道暴力匹配是通过对两个字符串进行每一个位置字符对比来查找匹配的上的子字符串。今天说的这个KR算法的思想和暴力匹配有些许类似,不过在实现上做了一些改进,这也是为什么说这个算法非常容易理解的原因,因为思路非常直接。
在计算机科学中,Rabin–Karp算法或Karp–Rabin算法(英文:Rabin–Karp algorithm或Karp–Rabin algorithm),是一种由理查德·卡普与迈克尔·拉宾于1987年提出的、使用散列函数以在文本中搜寻单个模式串的字符串搜索算法单次匹配。该算法先使用旋转哈希以快速筛出无法与给定串匹配的文本位置,此后对剩余位置能否成功匹配进行检验。此算法可推广到用于在文本搜寻单个模式串的所有匹配或在文本中搜寻多个模式串的匹配。
维基百科
按照惯例,对于被匹配的字符串称之为完全字符串,用于查找匹配的字符串称为为模式字符串。KR算法是通过计算散列值的方式从完全字符串中进行模式字符串的匹配,也就是我们经常说的哈希值。
KR从完全字符串的首位开始,计算和模式字符串长度一致的子字符串的哈希值,再通过哈希值与模式字符串计算得到的哈希值进行比较,如果哈希值不存在则字符串一定不相等。如果哈希值相等,两个字符串可能相等,这个时候就需要通过遍历对比两个字符串的每个字符,如果所有顺序字符都相等的话,则两个字符串相等。
为什么哈希值相等,但是值不一定相等,这里涉及到一个概念就是哈希碰撞,了解的童鞋直接跳过,不了解的童鞋听我举个例子,一年有365天,如果这个时候一个房间里有366个人,那么是不是一定会有两个人的生日的同一天,虽然生日相同,但是不是同一个人,其实哈希可以看成是固定长度的函数,而实际长度大于这个固定长度,所以值会重合,当然这个例子不是特别的准确,感兴趣的童鞋可以维基或者百度更准确的定义。
因此当两个长度一样的字符串计算出的哈希值一致的时候,还需要比对字符串对应位置上的所有字符,因此可以很简单的得出KR算法的实现代码。
func KarpRabinMatch(allString, modeString string) int {//计算模式字符串的哈希值hashMode := hash(modeString)//下标匹配结束end:= len(allString)-len(modeString)+1for i := 0; i < end ; i++ {//计算子字符串的哈希值hashKey := hash(allString[i : i+len(modeString)+1])if hashMode == hashKey {for j := 0; j < len(modeString); j++ {if allString[i+j] != modeString[j] {break}}return i}}return -1
}
可以看到代码中对模式字符串哈希值(hashMode)的计算只会处理一次,在循环中,从完全字符串的第一个字符开始的子字符串,计算对应哈希值,判断该哈希值与hashMode比较,如果不相等往后一位计算下一个子字符串的哈希值。
只要哈希值相等的情况下才会对比模式字符串的每一个字符,所以选择一个好的哈希函数,会使比较模式字符串每个字符的操作变得非常少,因此这个算法的时间复杂度在计算子字符串的哈希值上。如果子字符串的每个字符都要参与计算,完全字符串的所有字符需要计算长度n遍,每遍需要计算模式字符串的长度m个字符,因此时间复杂度为O(mn)。
02
—
旋转哈希
如上所说,如果每一次都要对子字符串的每个字符都进行计算,那么时间复杂度会达到O(mn),如果想要降低时间复杂度(提速),需要找到一种哈希方式,减少每次哈希计算的次数。于是针对这个字符串匹配算法,设计了一种简单的但是不优秀的哈希函数计算方式:旋转哈希。
旋转哈希(也称为滚动哈希、递归哈希、滚动校验和或滑动哈希)是一种哈希函数,输入的内容在一个窗口中进行移动哈希。
少数哈希函数允许快速计算滚动哈希值 — 只给出旧的哈希值,新的哈希值被快速计算出来,旧的值从窗口中移除,新的值添加到窗口中 — 类似于移动平均函数的计算方式,比其他低通滤波器更快。
维基百科
旋转哈希的想法很简单,有点类似窗口移动,每次向右移动窗口,把退出窗口的最左边字符的哈希值减掉,并且加上新加入窗口的最右边字符的哈希值,这样就达到了每次通过常数时间计算出哈希值。
如下所示,子字符串ABB的哈希值,hash1 = A + B + B,当窗口移动到BBE这个子字符串的时候,子字符串BBE的哈希值hash3 = hash1 - A + E即可。
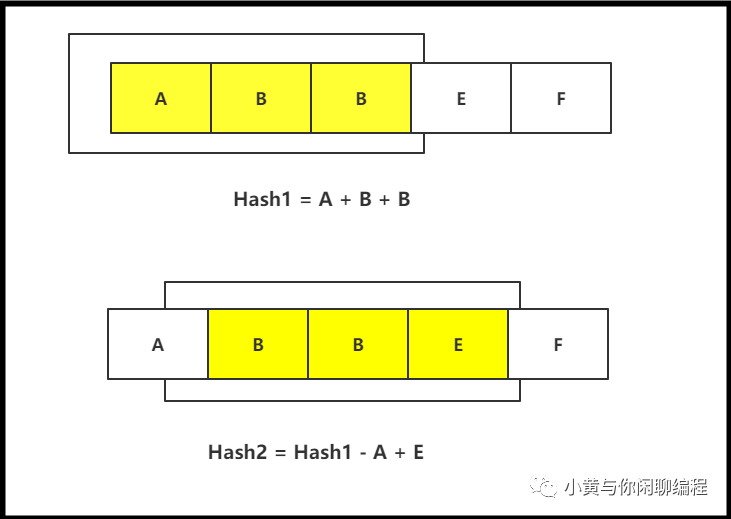
但是按照加法的这种方式去实现旋转哈希,产生哈希碰撞的概率非常高,比如说ABB和BBA的哈希值是一样的。这样就会导致不一样的字符串的哈希值相等,需要比较每一个字符,时间复杂度变高。
03
—
Rabin指纹
我们已经确定通过旋转哈希来实现KR算法,那么有什么更好的旋转哈希的计算方式能够产生更少的碰撞。这里要说的就是迈克尔·拉宾提出的Rabin指纹。
维基百科
Rabin指纹是通过程序解释多项式,通过当前字符串的多项式值,在窗口移动的时候,校验计算新的子字符串的结果值。它可以应用在一些分块数据的校验上,比如说网络传输包的校验和等。
04
—
多项式散列
计算哈希函数,如果模式字符串长度较长,通过多项式进行计算,可能会出现哈希值超过机器支持长度的情况,所以这边需要进行取余,简单来说就是在保证散列尽量平均分布的同时,不让长度溢出。
首先需要了解求余的特性:同余定理,在百度百科或者维基百科都可以找到对应的内容,其中有一条在我们的计算中会使用到,也就是:
同余式相乘:若a≡b(mod m),c≡d(mod m),则ac≡bd(mod m)
假设字符集大小为x,用质数y进行取模操作,用多项式散列进行哈希计算的表达式为:
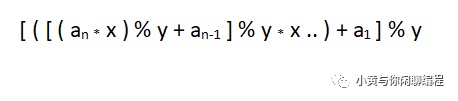
即假设当前字符串字符集大小为256,可以设置x = 256,质数 y = 101 来计算(当然设置其他数值也可以),比如说完全字符串为abcd,而匹配字符串长度为3。
首先计算子字符串abc的哈希值(字母通过ASCI码计算),即
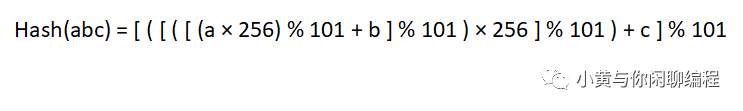
然后字符串窗口移动,计算bcde的哈希值,即
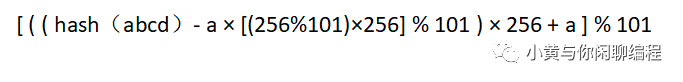
可以发现上面的两个哈希公式是减掉第一位的a的哈希值,然后再加上最后一位a的哈希值,通过旋转哈希的方式来实现常数时间内哈希值的计算。
对比上面两个公式,会发现 hash(abcd)中a的哈希值和下面计算减掉a的哈希值相差一个 %101,根据上面的同余式相乘公式可以得到,结果是一致的。
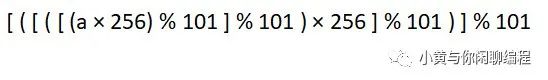
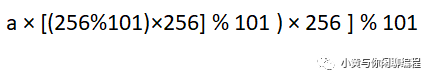
05
—
写在最后
KR算法虽然在单字符串的匹配中,算不上优秀的算法,但是如果在字符串中查找N个对应的模式,即多模式搜索中,KR算法的变种AC自动机的效率非常高。
本文涉及到的代码比较少,很多比较严谨的文字也是引用维基百科上面的解释,只是用了一些图片来诠释处理的过程。全文旨在说明一种思路和计算方式(旋转哈希),也许在之后工作中的某些场景会有所应用。
【往期回顾】
编码:震惊,让领导差点脑溢血的字符串匹配算法KMP
编码:horspool字符串匹配,折磨先生又来了
编码:sunday字符串匹配,“愉快”的一天又开始了
编码:Lumuto划分,实现快速选择
编码:前缀树工具
【参考资料】
旋转哈希
https://zh.wikipedia.org/wiki/%E6%97%8B%E8%BD%AC%E5%93%88%E5%B8%8C
Rabin–Karp算法
https://zh.wikipedia.org/wiki/Rabin%E2%80%93Karp%E7%AE%97%E6%B3%95
Rabin指纹
https://zh.wikipedia.org/wiki/Rabin%E6%8C%87%E7%BA%B9

这篇关于编码:KR字符串匹配,一个简单到领导都看得懂的算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







