本文主要是介绍Matlab|基于多目标粒子群算法的配电网储能选址定容,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、主要内容
二、主要流程
三、部分程序
四、程序结果
五、程序链接
一、主要内容
程序是对文章《基于多目标粒子群算法的配电网储能选址定容》的方法复现,具体内容如下:

以系统节点电压水平(电网脆弱性)、网络损耗以及储能系统总容量为目标建立了储能选址定容优化模型。求解过程中提出了一种改进多目标粒子群算法(improved multi—objective particle swarm optimizer,IMOPSO)。该算法根据粒子与种群最优粒子的距离来指导惯性权重的取值,使得各粒子的惯性权重可以自适应调整,并在二者距离较小时引入交叉变异操作,避免陷入局部最优解,同时采用动态密集距离排序来更新非劣解集并指导种群全局最优解的选取,在保持解集规模的同时使解的分布更均匀。为避免决策者偏好对最终结果的影响,采用基于信息熵的序数偏好法从最优Pareto解集中选取储能的最优接入方案。以IEEE33节点配电系统为例进行仿真验证,结果表明该方法在储能选址定容问题求解中具有很好的收敛性以及全局搜索能力。
二、主要流程
储能选址定容在智能算法中的实现过程不难,刚开始变量定义部分,主要是涉及储能选址的位置、容量和储能出力,以这两部分变量作为优化变量,通过设置最大值和最小值确定变量上下限范围。
下一步的关键点就是约束处理部分,对于储能soc约束,在单目标实现过程中可以采用罚函数的表达方式,但是在多目标求解过程中最好是采用绝对约束表达方式,因为多目标的帕累托解集有可能将不满足约束条件的目标值也筛选进入解集中,就会导致解集的不准确。
最后就是设置目标值,对于配电网节点系统,要注意潮流计算方式的选择和储能出力对系统影响,然后设置不同的目标值。
上述都设置清楚后,采用智能算法进行求解就简单了,多目标算法要注意采用拥挤距离识别方法保证解集分布的合理性(ps:之前有同学付费要解决解集分布不合理问题,被我拒绝了,直接发给他这个程序参考一下完美解决,这种方法已经很成熟,也有很多的参考,很容易解决,没必要花冤枉钱)。
三、部分程序
%% ***************导入网络参数******************%
FH1=[2084,1933,1782,1657,1564,1612,1982,2189,2412,2729,2905,3096,3189,3073,3000,2917,3149,3355,3526,3620,3715,3276,2911,2309];
% plot(FH1)%输入全天的负荷数据
WT1=[201,191,193,201,205,210,204,180,139,110,94,88,76,79,82,86,90,95,105,117,129,141,158,187]; %输入全天的风电数据
% plot(WT1)
PV1=[0,0,0,0,0,0,0,14,29,76,121,154,193,205,193,174,122,69,45,11,0,0,0,0]; %输入全天的光伏数据
% plot(PV1)
Generator=xlsread('GEN.xlsx','A2:U8'); %输入发电机矩阵参数,其中20,14接风电;9,30接光伏
Bus=xlsread('BUS.xlsx','A2:M34'); %输入负荷矩阵参数,matpower数据格式,第3列和第4列为有功和无功负荷所占总有功和无功负荷比例
FH=FH1/1000; %将kw化为mw,调整渗透率
WT=2*WT1/1000;
PV=2*PV1/1000;
FHBus=Bus;
T=24;
for t=1:T
FHP(:,t)=FH(1,t)*Bus(:,3); %求各个时间段的有功负荷
FHQ(:,t)=FH(1,t)*2.3/3.715*Bus(:,4); %求各个时间段的无功负荷【常数什么意思】
end
% *******************导入结束********************%
%% ****************决策空间的设置1**************%
maxFun=3; %三个目标函数
fff=[0,1;0.05,0.4;0.2,2]; %各个目标函数的最小值和最大值,即绝对正理想解和绝对负理想解,可分别设单目标求解
%fff=[0,0.4;30,100;10000,20000];
n = 50; % 初始种群个数
d = 52; % 空间维数,即决策变量(各设备控制量)个数
maxIterations = 50; % 最大迭代次数
wmax=0.9; %maximum of inertia factor,最大惯性系数
wmin=0.4; %minimum of inertia factor,最小惯性系数
c1=1.4962; %1.4962; %learning factor1,自我学习因子
c2=1.4962; %1.4962; %learning factor2,群体学习因子
soc=0.5;
X1limit = [2, 33]; % 设置选址参数限制
%X2limit = [0.2, 2.5]; % 设置容量参数限制,统一化成MW
X2limit = [1, 2]; % 设置容量参数限制,统一化成MW
V1limit = [-31, 31]; % 设置速度限制
%V2limit = [-2.3, 2.3]; % 设置速度限制
V2limit = [-1.8, 1.8];
Xmax=[X1limit(1,2),X1limit(1,2),X2limit(1,2),X2limit(1,2)];
Xmin=[X1limit(1,1),X1limit(1,1),X2limit(1,1),X2limit(1,1)];
dX=Xmax-Xmin;
Vmax=dX;
%***********决策空间设置1结束**********%
%% ******种群位置与速度初始化*******%
X1 = round(X1limit(1, 1) + (X1limit(1, 2) - X1limit(1, 1)) * rand(n, 2)); %初始种群的位置(节点位置)四舍五入取整
X2 = X2limit(1, 1)+(X2limit(1, 2)-X2limit(1, 1)) * rand(n, 2); %初始种群的位置(容量大小)
X = [X1,X2]; %初始种群的位置
V1 = V1limit(1, 2) * (2*rand(n, 2)-1); %初始种群的速度
V2 = V2limit(1, 2) * (2*rand(n, 2)-1); %初始种群的速度
V=[V1,V2]; % 初始种群的速度
%*****24小时储能出力变量初始化*********%
E1=zeros(n,T+1); %储能1各时段的剩余容量,即SOC
E2=zeros(n,T+1); %储能2各时段的容量
E1(:,1)=0.5*X(:,3); %初始容量设为50%总容量【拟采用40%】
E2(:,1)=0.5*X(:,4);
x1limit = [-0.5, 0.5]; % 设置储能有功出力约束
xmax=[Xmax,x1limit(1,2)*ones(1,48)];
xmin=[Xmin,x1limit(1,1)*ones(1,48)];
dx=xmax-xmin;
v1limit = [-1, 1]; % 设置储能有功出力约束
vmax=dx;
%******变量维数(总共52维)解释:位置1,位置2,额定容量1,额定容量2,储能1的24小时出力,储能2的24小时出力
x=[X,bsxfun(@times,x1limit(1,2)*ones(1,48),(2*rand(n, 48)-1))];
v=[V,bsxfun(@times,v1limit(1,2)*ones(1,48),(2*rand(n, 48)-1))];
四、程序结果

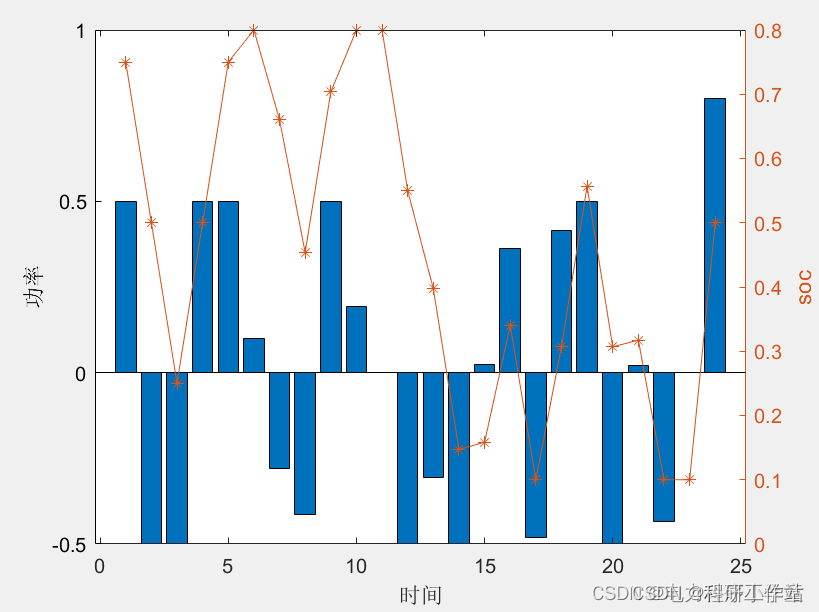
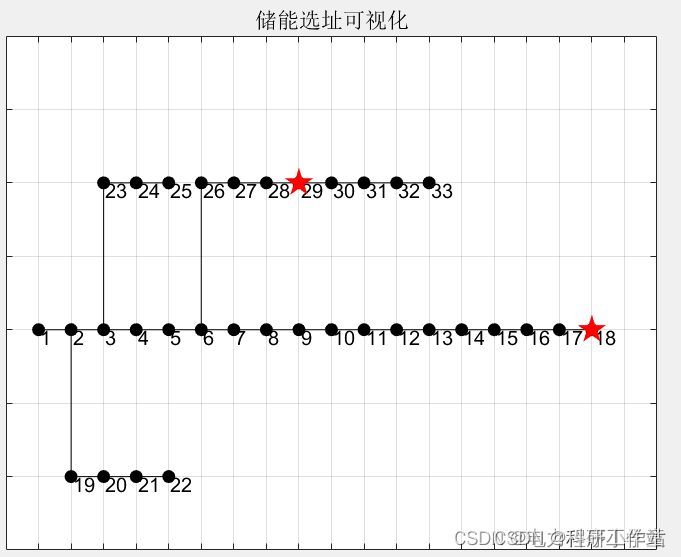
五、程序链接
这篇关于Matlab|基于多目标粒子群算法的配电网储能选址定容的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









