本文主要是介绍R语言检验独立性:卡方检验(Chi-square test)和费舍尔精确检验分析案例报告,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
统计测试最常见的领域之一是测试列联表中的独立性。在这篇文章中,我将展示如何计算列联表,我将在列联表中引入两个流行的测试:卡方检验和Fisher精确检验。
什么是列联表?
列联表提供关于两个分类变量的测量的整数计数。最简单的列联表是一个2 × 22×2 频率表,由两个变量产生,每个变量有两个级别:
| 组/观察 | 观察1 | 观察2 |
|---|---|---|
| 第1组 | ñ1 ,1ñ1,1 | ñ1 ,2ñ1,2 |
| 第2组 | ñ2 ,1ñ2,1 | ñ2 ,2ñ2,2 |
给定这样一个表格,问题是第1组是否表现出与第2组相比的观测频率。这些组代表因变量,因为它们依赖于自变量的观察。请注意,列联表必须是一种常见的误解2 × 22×2; 它们可以具有任意数量的维度,具体取决于变量显示的级别数。尽管如此,应避免对具有多个维度的列联表进行统计检验,因为除其他原因外,解释结果将具有挑战性。
数据集
要研究列联表的测试,我们将使用warpbreaks数据集:
<span style="color:#000000"><span style="color:#000000"><code>data(warpbreaks)
head(warpbreaks)</code></span></span>## breaks wool tension
## 1 26 A L
## 2 30 A L
## 3 54 A L
## 4 25 A L
## 5 70 A L
## 6 52 A L这是一个包含来自纺织行业的三个变量的数据集:中断描述了经线中断的次数,羊毛∈ { A ,B }羊毛∈{一个,乙} 描述了经过测试的羊毛类型 张力∈ { L ,M,H}张力∈{大号,中号,H}给出了施加在螺纹上的张力(低,中或高)。数据集中的每一行表示单个织机的测量值。为了解释不同织机的可变性,对羊毛和张力的每种组合进行了9次测量,数据集总共包含9 ⋅ 2 ⋅ 3 = 549⋅2⋅3=54 观察结果。
分析目标
我们想确定一种类型的羊毛在不同程度的紧张情况下是否优于另一种羊毛。为了研究我们是否可以找到一些差异的证据,让我们来看看数据:
为了研究链断裂数的差异,让我们可视化数据:
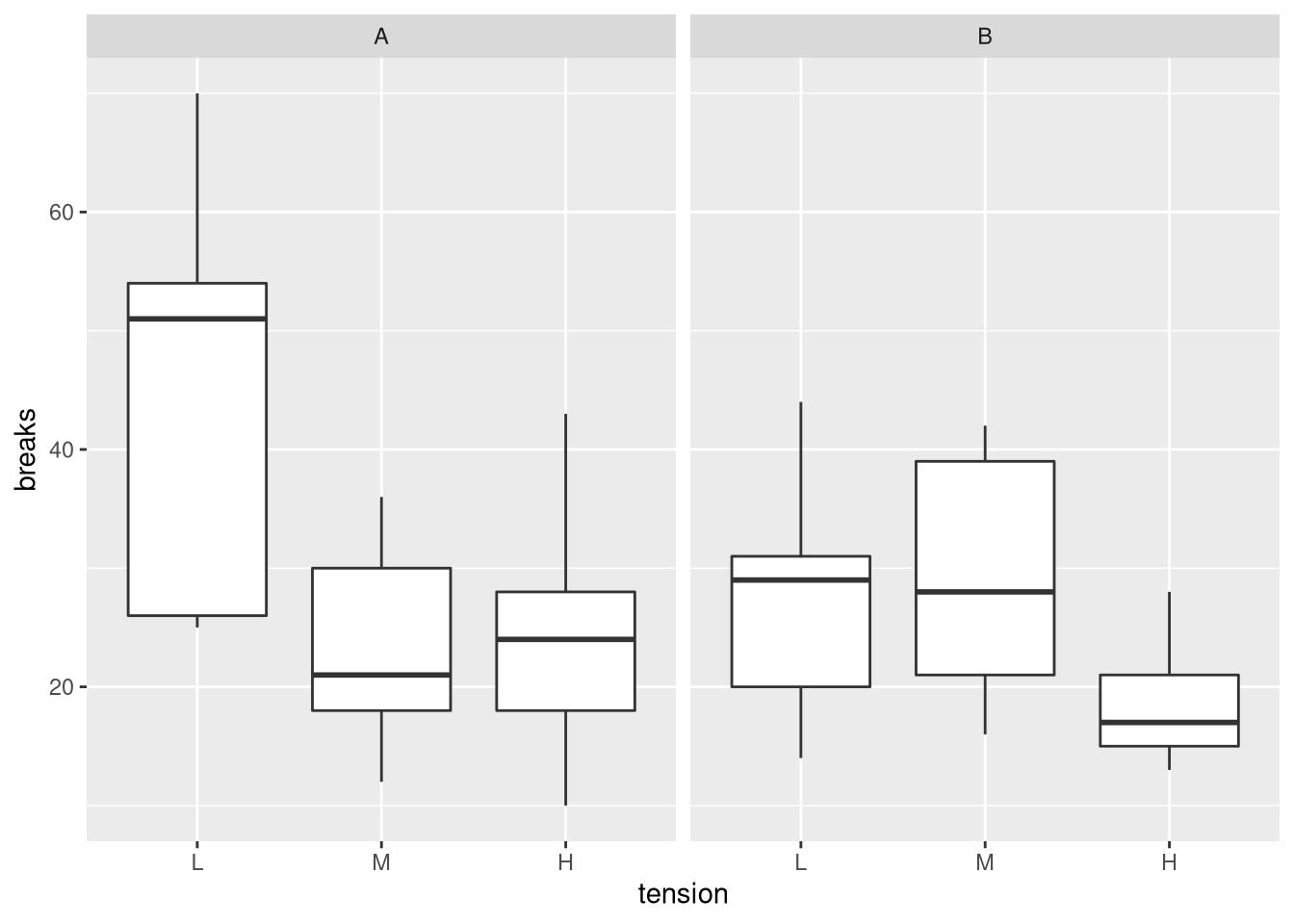
从图中我们可以看出,总体而言,羊毛B与较少的断裂相关联。羊毛A似乎特别低劣,因为低张力。
转换为列联表
为了获得列联表,我们首先需要总结两种类型的羊毛和三种类型的张力的不同织机的断裂。
## wool tension breaks
## 1 A L 401
## 2 A M 216
## 3 A H 221
## 4 B L 254
## 5 B M 259
## 6 B H 169然后我们使用xtabs(发音为交叉表)函数来生成列联表:
## tension
## wool L M H
## A 401 216 221
## B 254 259 169现在,df我们有了应用统计测试所需的结构。
统计检验
用于确定来自不同组的测量值是否独立的两种最常见的测试是卡方检验(χ2χ2测试)和费舍尔的精确测试。请注意,如果测量结果配对,则应使用McNemar测试(例如,可以识别单个织机)。
皮尔逊的卡方检验
该 χ2χ2test是一种非参数测试,可应用于具有各种维度的列联表。测试的名称源自χ2χ2分布,即独立标准正态变量的平方分布。这是测试统计的分布χ2χ2 测试,由卡方值的总和定义 χ2我,jχ一世,Ĵ2 对于所有细胞对 我,j一世,Ĵ 由细胞观察值之间的差异引起的 Ø我,jØ一世,Ĵ 和期望值 Ë我,jË一世,Ĵ,归一化 Ë我,jË一世,Ĵ:
&Sigma; χ2我,j哪里χ2我,j= (O我,j- E.我,j)2Ë我,jΣχ一世,Ĵ2哪里χ一世,Ĵ2=(Ø一世,Ĵ- Ë一世,Ĵ)2Ë一世,Ĵ
这里的直觉是 &Sigma; χ2我,jΣχ一世,Ĵ2 如果观测值明显偏离预期值,则会很大 &Sigma; χ2我,jΣχ一世,Ĵ2如果观测值与预期值很好地吻合,则接近于零。通过执行测试
## [1] 7.900708e-07由于p值小于0.05,我们可以在5%显着性水平上拒绝测试的零假设(断裂的频率独立于羊毛)。根据df一个人的条目,然后可以声称羊毛B比羊毛A明显更好(相对于经纱断裂)。
调查Pearson残差
另一种方法是考虑测试的卡方值。该chisq.test函数提供卡方值的Pearson残差(根),即χ我,jχ一世,Ĵ。与由平方差异产生的卡方值相反,残差不是平方的。因此,残差反映了观测值超过预期值(正值)或低于预期值(负值)的程度。在我们的数据集中,正值表示比预期更多的链断裂,而负值表示更少的断点:
## tension
## wool L M H
## A 2.0990516 -2.8348433 0.4082867
## B -2.3267672 3.1423813 -0.4525797残留物表明,与羊毛A相比,羊毛B的低张力和高张力断裂比预期的要少。然而,对于中等张力,羊毛B比预期的断裂更多。再次,我们发现,整体羊毛B优于羊毛A.残留物的值也表明羊毛B对于低张力(残差为2.1),高张力(0.41)和中等张力严重( - 2.8)。然而,残留物有助于我们识别羊毛B的问题:它对中等张力的表现不佳。这将如何促进进一步发展?为了获得在所有张力水平下表现良好的羊毛,我们需要专注于改善羊毛B的中等张力。为此,我们可以考虑使羊毛A在中等张力下表现更好的特性。
费舍尔的确切测试
Fisher的精确测试是用于测试独立性的非参数测试,通常仅用于测试 2 × 22×2列联表。作为精确显着性检验,Fisher检验符合所有假设,在此基础上定义检验统计量的分布。实际上,这意味着错误拒绝率等于测试的显着性水平,对于近似测试,例如χ2χ2测试。简而言之,Fisher的精确测试依赖于使用二项式系数根据超几何分布计算p值,即通过
p = (n1 ,1+ n1 ,2ñ1 ,1)(n2 ,1+ n2 ,2ñ2 ,1)(n1 ,1+ n1 ,2+ n2 ,1+ n2 ,2ñ1 ,1+ n2 ,1)p=(ñ1,1+ñ1,2ñ1,1)(ñ2,1+ñ2,2ñ2,1)(ñ1,1+ñ1,2+ñ2,1+ñ2,2ñ1,1+ñ2,1)
由于计算的因子可能变得非常大,Fisher精确检验可能不适用于大样本量。
请注意,无法指定测试的替代方法,df因为优势比(表示效果大小)仅定义为2 × 22×2 矩阵:
O R = n1 ,1ñ1 ,2/ n2 ,1ñ2 ,2Ø[R=ñ1,1ñ1,2/ñ2,1ñ2,2
我们仍然可以执行Fisher精确检验以获得p值:
## [1] 8.162421e-07得到的p值类似于从中获得的p值 χ2χ2 测试并得出相同的结论:我们可以拒绝零假设,即羊毛的类型与不同应力水平下观察到的断裂次数无关。
转换为2乘2矩阵
为了指定备选假设并获得优势比,我们可以计算三者的测试 2 × 22×2可以构造的矩阵df:
由于替代方案设置得更大,这意味着我们正在进行单尾测试,其中另一种假设是羊毛A与羊毛B的断裂次数相关(即我们预期O R > 1Ø[R>1)。通过执行测试2 × 22×2表格,我们也获得了解释性:我们现在可以区分羊毛不同的具体条件。然而,在解释p值之前,我们需要纠正多个假设检验。在这种情况下,我们进行了三次测试。在这里,我们只需将0.05的初始显着性水平调整为0.053= 0.01 6¯¯¯0.053=0.016¯根据Bonferroni方法。根据调整后的阈值,以下测试显着:
## [1] "L vs others"这一发现表明,如果应力较轻,羊毛B仅显着优于羊毛A. 请注意,我们也可以采用构建方法2 × 22×2 矩阵 χ2χ2测试。随着χ2χ2 然而,测试并不是必要的,因为我们的分析基于残差。
摘要:卡方对费舍尔的精确检验
以下是两个测试的属性摘要:
| 标准 | 卡方检验 | 费舍尔的确切测试 |
|---|---|---|
| 最小样本量 | 大 | 小 |
| 准确性 | 近似 | 精确 |
| 列联表 | 任意维度 | 通常为2x2 |
| 解释 | 皮尔逊残差 | 优势比 |
通常,Fisher精确检验优于卡方检验,因为它是一种精确检验。如果单个细胞的观察结果很少(例如小于10),则应特别避免卡方检验。由于Fisher的精确检验对于大样本量和精确度可能在计算上是不可行的χ2χ2 测试随着样本数量的增加而增加 χ2χ2在这种情况下,测试是合适的替代品。另一个优点了χ2χ2 测试是它更适合维数超过的列联表 2 × 22×2。
有问题吗?欢迎留言
这篇关于R语言检验独立性:卡方检验(Chi-square test)和费舍尔精确检验分析案例报告的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





