CMU 10-414/714: Deep Learning Systems --hw3

2024-03-20 07:28
文章标签 deep learning 714 systems cmu hw3 414

本文主要是介绍CMU 10-414/714: Deep Learning Systems --hw3，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

实现功能

  1. 在ndarray.py文件中完成一些python array操作
    • 我们实现的NDArray底层存储就是一个一维向量，只不过会有一些额外的属性（如shape、strides）来表明这个flat array在维度上的分布。底层运算（如加法、矩阵乘法）都是用C++写的，以便达到理论上的最高速度。但像转置、broadcasting、矩阵求子阵等操作都可以在python框架里通过简单的调整array的属性（如strides）来实现
    • 实现的python array功能：这四个功能都不需要重新分配内存，而是在原array的基础上修改shape/strides/etc来实现一些变形（除了第四个__getitem__()，它并不修改array的形状）
      • reshape(new_shape)：调用as_strided(new_shape, strides)，再调用make(new_shape, strides, device=self.device, handle=self._handle)。（其中as_strided会额外检查一下shape的长度是否等于strides的长度，strides的数值是通过self.compact_strides(new_shape)算出来的）
      • permute(new_axes)：调换array的维度顺序。按照new_axes的顺序调换self.strides以及self.shape得到new_shape和new_strides，最后再调用self.as_strided"(new_shape, new_strides)
      • broadcast_to()：对于原shape中为1的维度，将其步幅设为0，然后调用as_strided(new_shape, new_strides)，然后as_strided调用make(new_shape, new_strides, device=self.device, handle=self._handle)。即重新make，修改其中的shape和stride，但内存位置不变（即handle不变）。至于这里将stride部分设为0，猜测更底层有代码处理这里，但我目前还没找到
      • __getitem__(idxs)：这是一个非常好的理解我们所实现的NDArray的例子，前面也说了，底层的array存储就是一个一维向量，是通过shape、stride、offset这些属性来指示该向量的维度的。本例就是在原array的基础上求子矩阵，且不改变其内存位置，就是通过一系列计算得到新的new_offset、new_shape、new_stride，就可以将原本的大矩阵重新解释成一个小矩阵。图示如下
        在这里插入图片描述
        而这里也天然解释了什么是紧凑型（compact）矩阵和非紧凑型矩阵：上述原矩阵就是紧凑型的，切片后形成的蓝底矩阵就是非紧凑型的。
        而这也带出了下一个问题：如何选择原矩阵的一个子矩阵进行修改内容。因为本课程中几乎所有setitem操作都会先调用.compact()，而这会导致从原矩阵中copy子矩阵到一个新的内存空间，这显然不是__setitem__()所期望的，因此要大动干戈。
  2. 【CPU】compact和setitem
    其实这里的实现主要就是根据这个原理：out[cnt++] = in[strides[0]*i + strides[1]*j + strides[2]*k];（这里是按三维矩阵算的，下面的代码通过while循环可以扩展到其他维度）
    • Compact：就是将原来的非紧凑型矩阵a变成紧凑型矩阵out，具体是根据输入的shape、strides、offset（以a为主体确定的），将a中的子矩阵提出来，将各位置的值赋给另一个矩阵out。下面的mode是INDEX_IN，即调用_strided_index_setter(&a, out, shape, strides, offset, INDEX_IN); 
      // 从后往前每一个维度，都根据该维度的步长、offset以及循环次数来确定本次要copy矩阵a的哪一个元素
// 其实就是根据strides、offset来确定一维下的index
void _strided_index_setter(const AlignedArray* a, AlignedArray* out, std::vector<uint32_t> shape,std::vector<uint32_t> strides, size_t offset, strided_index_mode mode, int val=-1) {int depth = shape.size();std::vector<uint32_t> loop(depth, 0);int cnt = 0;while (true) {// inner loopint index = offset;for (int i = 0; i < depth; i++) {index += strides[i] * loop[i];}switch (mode) {case INDEX_OUT: out->ptr[index] = a->ptr[cnt++]; break;case INDEX_IN: out->ptr[cnt++] = a->ptr[index]; break;case SET_VAL: out->ptr[index] = val; break;}// incrementloop[depth - 1]++;// carryint idx = depth - 1;while (loop[idx] == shape[idx]) {if (idx == 0) {// overflowreturn;}loop[idx--] = 0;loop[idx]++;}}
}
    • EwiseSetitem(a, out, shape, strides, offset)：这里a是紧凑型矩阵，out是一个非紧凑行矩阵，需要将a的各元素的值赋给out的指定位置上（根据shape、strides、offset确定）。只需要复用上面的代码，将mode改为INDEX_OUT，即调用_strided_index_setter(&a, out, shape, strides, offset, INDEX_OUT);
    • ScalarSetitem(size, val, out, shape, strides, offset)：out是一个非紧凑型子矩阵，根据shape、strides、offset在out的对应位置将值写为val，即调用_strided_index_setter(nullptr, out, shape, strides, offset, SET_VAL, val);
  3. 【CPU】Elementwise和scalar操作
    这个就非常简单了，根据矩阵的size属性遍历其每个元素即可
  4. 【CPU】Reductions
    这个也很简单，条件是矩阵的底层存储都是一维、行优先的。这类里有两个函数：ReduceSum和ReduceMax，其参数都是原矩阵a、输出矩阵out、reduce_size，其中a.size = out.size * reduce_size。看代码就懂了
    • ReduceMax：
      void ReduceMax(const AlignedArray& a, AlignedArray* out, size_t reduce_size) {for (int i = 0; i < out->size; i++) {scalar_t max = a.ptr[i * reduce_size];for (int j = 0; j < reduce_size; j++) {max = std::max(max, a.ptr[i * reduce_size + j]);}out->ptr[i] = max;}
}
    • ReduceSum：
      void ReduceSum(const AlignedArray& a, AlignedArray* out, size_t reduce_size) {for (int i = 0; i < out->size; i++) {scalar_t sum = 0;for (int j = 0; j < reduce_size; j++) {sum += a.ptr[i * reduce_size + j];}out->ptr[i] = sum;}
}
  5. 【CPU】矩阵乘
    • 朴素矩阵乘Matmul：
      void Matmul(const AlignedArray& a, const AlignedArray& b, AlignedArray* out, uint32_t m, uint32_t n,uint32_t p) {for (int i = 0; i < m; i++) {for (int j = 0; j < p; j++) {out->ptr[i * p + j] = 0;for (int k = 0; k < n; k++) {out->ptr[i * p + j] += a.ptr[i * n + k] * b.ptr[k * p + j];}}}
}
    • MatmulTiled和AlignedDot：前者负责根据分片大小计算目前参与运算的是a、b、out的哪些元素（哪部分block）；后者根据前者传进来的block进行计算（a分片与b分片进行矩阵乘法得到out分片
      void MatmulTiled(const AlignedArray& a, const AlignedArray& b, AlignedArray* out, uint32_t m,uint32_t n, uint32_t p) {for (int i = 0; i < m * p; i++) out->ptr[i] = 0;for (int i = 0; i < m / TILE; i++) {for (int j = 0; j < p / TILE; j++) {for (int k = 0; k < n / TILE; k++) {AlignedDot(&a.ptr[i * n * TILE + k * TILE * TILE], &b.ptr[k * p * TILE + j * TILE * TILE], &out->ptr[i * p * TILE + j * TILE * TILE]);}}}
}

      inline void AlignedDot(const float* __restrict__ a,const float* __restrict__ b,float* __restrict__ out) {a = (const float*)__builtin_assume_aligned(a, TILE * ELEM_SIZE);b = (const float*)__builtin_assume_aligned(b, TILE * ELEM_SIZE);out = (float*)__builtin_assume_aligned(out, TILE * ELEM_SIZE);for (int i = 0; i < TILE; i++) {for (int j = 0; j < TILE; j++) {for (int k = 0; k < TILE; k++) {out[i * TILE + j] += a[i * TILE + k] * b[k * TILE + j];}}}
}
      过程原理图：
      在这里插入图片描述
      这里有一个疑问，a、b虽然每次通过MatmulTiled计算的分片的起始位置是正确的，但是如何保证连续的Tile*Tile分块元素就是如图所示那样的呢。按理说a、b的底层存储应该是连续的行优先，那（按照tile=2算）a[2]、a[3]、b[2]、b[3]应该是按行走下去而不是取下一行啊。待解答…
  6. 【CUDA】compact和setitem
    • compact：
      __device__ size_t index_transform(size_t index, CudaVec shape, CudaVec strides, size_t offset) {size_t idxs[MAX_VEC_SIZE];size_t cur_size, pre_size = 1;// 将给定的线性索引映射回多维数组的索引，即计算index值在各维度上对应是第几个// 思路就是从后往前遍历shape，cur_size表示当前处理的维度由几个元素构成// index%cur_size/pre_size就表示在当前维度的第几个分量// index%cur_size表示是当前维度（只看当前维）的第几个元素，再/pre_size就表示是当前维度的第几块for (int i = shape.size - 1; i >= 0; i--) {cur_size = pre_size * shape.data[i]; idxs[i] = index % cur_size / pre_size;pre_size = cur_size;}// 根据上述算好的多维数组索引，计算在原非紧凑型矩阵中的线性索引size_t comp_idx = offset;for (int i = 0; i < shape.size; i++) comp_idx += idxs[i] * strides.data[i];return comp_idx;
}__global__ void CompactKernel(const scalar_t* a, scalar_t* out, size_t size, CudaVec shape,CudaVec strides, size_t offset) {size_t gid = blockIdx.x * blockDim.x + threadIdx.x;/// BEGIN YOUR SOLUTIONif (gid < size)out[gid] = a[index_transform(gid, shape, strides, offset)];/// END YOUR SOLUTION
}void Compact(const CudaArray& a, CudaArray* out, std::vector<uint32_t> shape,std::vector<uint32_t> strides, size_t offset) {CudaDims dim = CudaOneDim(out->size);CompactKernel<<<dim.grid, dim.block>>>(a.ptr, out->ptr, out->size, VecToCuda(shape),VecToCuda(strides), offset);
}
      图示如下：
      在这里插入图片描述
    • EWiseSetitem：
      __global__ void EwiseSetitemKernel(const scalar_t* a, scalar_t* out, size_t size, CudaVec shape,CudaVec strides, size_t offset) {size_t gid = blockIdx.x * blockDim.x + threadIdx.x;if (gid < size)out[index_transform(gid, shape, strides, offset)] = a[gid];
}void EwiseSetitem(const CudaArray& a, CudaArray* out, std::vector<uint32_t> shape,std::vector<uint32_t> strides, size_t offset) {/// BEGIN YOUR SOLUTIONCudaDims dim = CudaOneDim(out->size);EwiseSetitemKernel<<<dim.grid, dim.block>>>(a.ptr, out->ptr, a.size, VecToCuda(shape),VecToCuda(strides), offset);/// END YOUR SOLUTION
}
    • ScalarSetitem：
      __global__ void ScalarSetitemKernel(size_t size, scalar_t val, scalar_t* out, CudaVec shape, CudaVec strides, size_t offset) {size_t gid = blockIdx.x * blockDim.x + threadIdx.x;if (gid < size)out[index_transform(gid, shape, strides, offset)] = val;
}void ScalarSetitem(size_t size, scalar_t val, CudaArray* out, std::vector<uint32_t> shape,std::vector<uint32_t> strides, size_t offset) {/// BEGIN YOUR SOLUTIONCudaDims dim = CudaOneDim(out->size);ScalarSetitemKernel<<<dim.grid, dim.block>>>(size, val, out->ptr, VecToCuda(shape),VecToCuda(strides), offset);/// END YOUR SOLUTION
}
      • 其实总结一下，CPU版的将紧凑小矩阵的index转换成非紧凑大矩阵的index，是在一个loop中实现的，并在loop中找到index后就完成了copy工作；对于GPU版来说，是将copy工作分配给各个线程，因此若要让每个线程都能正确copy，还需要每个线程根据自己分配到的紧凑小矩阵的index，计算得到非紧凑大矩阵的index。即每个线程完成CPU版中一个loop的操作（但不需要后续的检查）。
  7. 【CUDA】Elementwise和scalar操作
    和CPU版本的一样，也很简单。且这part非常能体现CUDA的并行、高效特性。举个例子：
    __global__ void EwiseMulKernel(const scalar_t* a, const scalar_t* b, scalar_t* out, size_t size){size_t gid = blockInx.x * blockDim.x + threadIdx.x;if (gid<size){out[gid] = a[gid] * b[gid];}
}
void EwiseMul(const CudaArray &a, const CudaArray &b, CudaArray* out){CudaDims dim = CudaOneDim(out->size);EwiseMulKernel<<<dim.grid, dim.block>>>(a.ptr, b.ptr, out->ptr, out->size);
}
  8. 【CUDA】Reductions
    • ReduceMax
      __global__ void ReduceMaxKernel(const scalar_t* a, scalar_t* out, size_t reduce_size, size_t size){size_t gid = blockIdx.x * blockDim.x + threadIdx.x;if (gid<size){size_t offset = gid * reduce_size;scalar_t reduce_max = a[offset];for (int i=1; i<reduce_size; i++){reduce_max = max(reduce_max, a[offset+i]);}out[gid] = reduce_max;}
}void ReduceMax(const CudaArray& a, CudaArray* out, size_t reduce_size) {CudaDims dim = CudaOneDim(out->size);ReduceMaxKernel<<<dim.grid, dim.block>>>(a.ptr, out->ptr, reduce_size, out->size);
}
    • ReduceSum
  9. 【CUDA】矩阵乘
    使用朴素矩阵乘即可，一个线程负责out矩阵的一个元素
    __global__ void MatmulKernel(const scalar_t* a, const scalar_t* b, scalar_t* out, uint32_t M,uint32_t N, uint32_t P) {size_t i = blockIdx.x * blockDim.x + threadIdx.x; size_t j = blockIdx.y * blockDim.y + threadIdx.y;if (i < M && j < P) {out[i * P + j] = 0;for (int k = 0; k < N; k++) {out[i * P + j] += a[i * N + k] * b[k * P + j];}}
}
void Matmul(const CudaArray& a, const CudaArray& b, CudaArray* out, uint32_t M, uint32_t N,uint32_t P) {dim3 grid(BASE_THREAD_NUM, BASE_THREAD_NUM, 1);dim3 block((M + BASE_THREAD_NUM - 1) / BASE_THREAD_NUM, (P + BASE_THREAD_NUM - 1) / BASE_THREAD_NUM, 1);MatmulKernel<<<grid, block>>>(a.ptr, b.ptr, out->ptr, M, N, P);
}
    线程分布如下：
    在这里插入图片描述

补充知识

一、CUDA相关代码

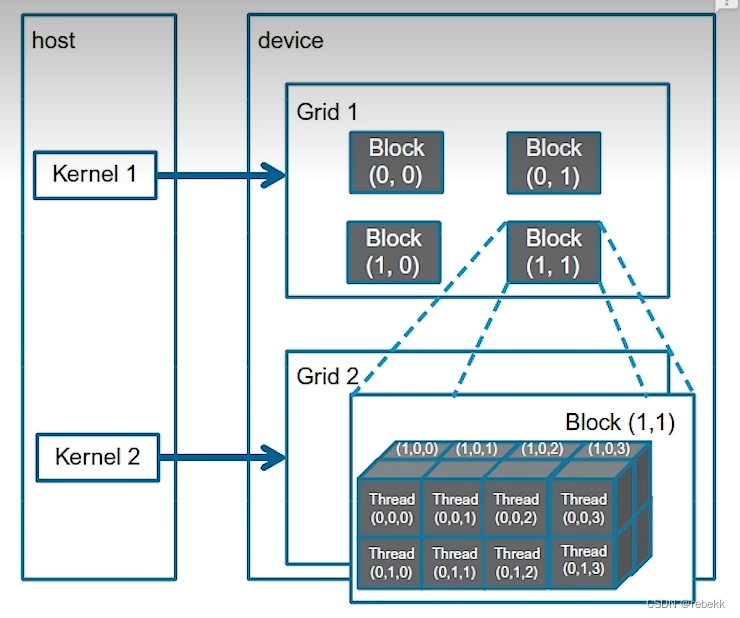
在这里插入图片描述
如上图的结构，首先定义Cuda的维度：

struct CudaDims {dim3 block, grid;
};

根据数据数量来判定需要多少个block、多少个thread（都是一个维度下的）

CudaDims CudaOneDim(size_t size) {/*** Utility function to get cuda dimensions for 1D call*/CudaDims dim;size_t num_blocks = (size + BASE_THREAD_NUM - 1) / BASE_THREAD_NUM;dim.block = dim3(BASE_THREAD_NUM, 1, 1);  // 一个block里的线程dim.grid = dim3(num_blocks, 1, 1);  // 一个grid里的blockreturn dim;
}

这篇关于CMU 10-414/714: Deep Learning Systems --hw3的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/828718。

相关文章

vue解决子组件样式覆盖问题scoped deep

vue解决子组件样式覆盖问题scoped deep

《vue解决子组件样式覆盖问题scopeddeep》文章主要介绍了在Vue项目中处理全局样式和局部样式的方法,包括使用scoped属性和深度选择器（/deep/）来覆盖子组件的样式,作者建议所有组件... 目录前言scoped分析deep分析使用总结所有组件必须加scoped父组件覆盖子组件使用deep前言
阅读更多...
LeetCode 第414场周赛个人题解

LeetCode 第414场周赛个人题解

目录 Q1. 将日期转换为二进制表示 原题链接 思路分析 AC代码 Q2. 范围内整数的最大得分 原题链接 思路分析 AC代码 Q3. 到达数组末尾的最大得分 原题链接 思路分析 AC代码 Q4. 吃掉所有兵需要的最多移动次数 原题链接 思路分析 AC代码 Q1. 将日期转换为二进制表示 原题链接 Q1. 将日期转换为二进制表示 思路分析
阅读更多...
简单的Q-learning|小明的一维世界(3)

简单的Q-learning|小明的一维世界(3)

简单的Q-learning|小明的一维世界(1) 简单的Q-learning|小明的一维世界(2) 一维的加速度世界 这个世界，小明只能控制自己的加速度，并且只能对加速度进行如下三种操作：增加1、减少1、或者不变。所以行动空间为： { u 1 = − 1 , u 2 = 0 , u 3 = 1 } \{u_1=-1, u_2=0, u_3=1\} {u1​=−1,u2​=0,u3​=1}
阅读更多...
简单的Q-learning|小明的一维世界(2)

简单的Q-learning|小明的一维世界(2)

上篇介绍了小明的一维世界模型 、Q-learning的状态空间、行动空间、奖励函数、Q-table、Q table更新公式、以及从Q值导出策略的公式等。最后给出最简单的一维位置世界的Q-learning例子，从给出其状态空间、行动空间、以及稠密与稀疏两种奖励函数的设置方式。下面将继续深入，GO！ 一维的速度世界 这个世界，小明只能控制自己的速度，并且只能对速度进行如下三种操作：增加1、减
阅读更多...
Deep Ocr

Deep Ocr

1.圈出内容,文本那里要有内容.然后你保存,并'导出数据集'. 2.找出deep_ocr_recognition_training_workflow.hdev 文件.修改“DatasetFilename := 'Test.hdict'” 310行 write_deep_ocr (DeepOcrHandle, BestModelDeepOCRFilename) 3.推理test.hdev
阅读更多...
CMU 10423 Generative AI：HW0

CMU 10423 Generative AI：HW0

由于找不到S24版数据集，所以HW0用的F24版的。 项目地址见：https://github.com/YM2025/CMU_10423_2024S 文章目录 0 作业概述1 阅读（3分）2 图像分类（43分）2.1 (3 分)【完成】2.2 (3 分)【完成】2.3 (4 分)【完成】2.4 (4 分)【完成】2.5【完成】2.5.a (3 分)2.5.b (2 分) 2.6 (2 分)
阅读更多...
Learning Memory-guided Normality for Anomaly Detection——学习记忆引导的常态异常检测

Learning Memory-guided Normality for Anomaly Detection——学习记忆引导的常态异常检测

又是一篇在自编码器框架中研究使用记忆模块的论文，可以看做19年的iccv的论文的衍生，在我的博客中对19年iccv这篇论文也做了简单介绍。韩国人写的，应该是吧，这名字听起来就像。 摘要abstract 我们解决异常检测的问题，即检测视频序列中的异常事件。基于卷积神经网络的异常检测方法通常利用代理任务(如重建输入视频帧)来学习描述正常情况的模型，而在训练时看不到异常样本，并在测试时使用重建误
阅读更多...
Learning Temporal Regularity in Video Sequences——视频序列的时间规则性学习

Learning Temporal Regularity in Video Sequences——视频序列的时间规则性学习

Learning Temporal Regularity in Video Sequences CVPR2016 无监督视频异常事件检测早期工作 摘要 由于对“有意义”的定义不明确以及场景混乱，因此在较长的视频序列中感知有意义的活动是一个具有挑战性的问题。我们通过在非常有限的监督下使用多种来源学习常规运动模式的生成模型（称为规律性）来解决此问题。体来说，我们提出了两种基于自动编码器的方法，以
阅读更多...
COD论文笔记 Adaptive Guidance Learning for Camouflaged Object Detection

COD论文笔记 Adaptive Guidance Learning for Camouflaged Object Detection

论文的主要动机、现有方法的不足、拟解决的问题、主要贡献和创新点如下： 动机： 论文的核心动机是解决伪装目标检测（COD）中的挑战性任务。伪装目标检测旨在识别和分割那些在视觉上与周围环境高度相似的目标，这对于计算机视觉来说是非常困难的任务。尽管深度学习方法在该领域取得了一定进展，但现有方法仍面临有效分离目标和背景的难题，尤其是在伪装目标与背景特征高度相似的情况下。 现有方法的不足之处： 过于
阅读更多...
One-Shot Imitation Learning

One-Shot Imitation Learning

发表时间：NIPS2017 论文链接：https://readpaper.com/pdf-annotate/note?pdfId=4557560538297540609&noteId=2424799047081637376 作者单位：Berkeley AI Research Lab, Work done while at OpenAI Yan Duan†§ , Marcin Andrychow
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2