http://blog.csdn.net/pipisorry/article/details/51106570
最优化函数库Optimization
优化是找到最小值或等式的数值解的问题。scipy.optimization子模块提供了函数最小值(标量或多维)、曲线拟合和寻找等式的根的有用算法。
from scipy import optimize皮皮blog
最小二乘拟合
假设有一组实验数据(xi,yi ), 事先知道它们之间应该满足某函数关系yi=f(xi),通过这些已知信息,需要确定函数f的一些参数。例如,如果函数f是线性函数f(x)=kx+b,那么参数 k和b就是需要确定的值。如果用p表示函数中需要确定的参数,那么目标就是找到一组p,使得下面的函数S的值最小:
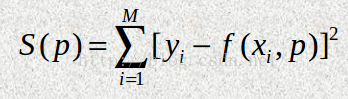
这种算法被称为最小二乘拟合(Least-square fitting)。
在optimize模块中可以使用leastsq()对数据进行最小二乘拟合计算。leastsq() 只需要将计算误差的函数和待确定参数 的初始值传递给它即可。
leastsq()函数传入误差计算函数和初始值,该初始值将作为误差计算函数的第一个参数传入;
计算的结果r是一个包含两个元素的元组,第一个元素是一个数组,表示拟合后的参数k、b;第二个元素如果等于1、2、3、4中的其中一个整数,则拟合成功,否则将会返回mesg。
示例
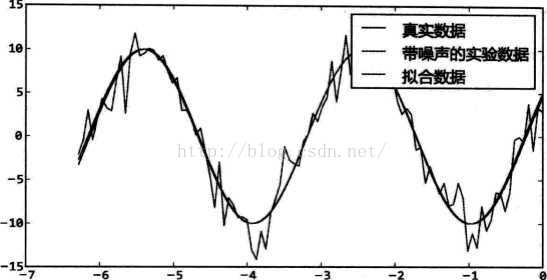
使用最小二乘法对带噪声的正玄波数据进行拟合:"""
使用leastsq()对带噪声的正弦波数据进行拟合。拟合所得到的参数虽然和实际的参数有可能完全不同,但是由于正弦函数具有周期性,实际上拟合的结果和实际的函数是一致的。
"""
import numpy as np
from scipy.optimize import leastsq
def func(x, p):
"""
数据拟合所用的函数: A*sin(2*pi*k*x + theta)
"""
A, k, theta = p
return A*np.sin(2*np.pi*k*x+theta)
def residuals(p, y, x):
"""
实验数据x, y和拟合函数之间的差,p为拟合需要找到的系数
"""
return y - func(x, p)
x = np.linspace(-2*np.pi, 0, 100)
A, k, theta = 10, 0.34, np.pi/6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
# 加入噪声之后的实验数据
y1 = y0 + 2 * np.random.randn(len(x))
p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数
# 调用leastsq进行数据拟合, residuals为计算误差的函数
# p0为拟合参数的初始值,# args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))
# 除了初始值之外,还调用了args参数,用于指定residuals中使用到的其他参数(直线拟合时直接使用了X,Y的全局变量),同样也返回一个元组,第一个元素为拟合后的参数数组;
这里将 (y1, x)传递给args参数。Leastsq()会将这两个额外的参数传递给residuals()。因此residuals()有三个参数,p是正弦函数的参数,y和x是表示实验数据的数组。
print u"真实参数:", [A, k, theta]
print u“拟合参数”, plsq[0] # 实验数据拟合后的参数
import pylab as pl
pl.plot(x, y0, label=u"真实数据")
pl.plot(x, y1, label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), label=u"拟合数据")
pl.legend()
pl.show()
>>> 真实参数: [10, 0.34000000000000002, 0.52359877559829882]
>>> 拟合参数[-9.84152775 0.33829767 -2.68899335]
皮皮blog
标量函数的最小值
Local Optimization
minimize_scalar(fun[, bracket, bounds, ...])Minimization of scalar function of one variable.
nfev: 9
nit: 8
success: True
x: 1.333333333395553
def test():
import mathfrom scipy import optimizefunc = lambda x: x * math.log(x, 2)a = optimize.minimize_scalar(func, bounds=[0.1, 1], method='bounded')print(a)message: 'Solution found.'
nfev: 9
status: 0
success: True
x: 0.3678794534141907
trunc = [0, 4]max_x = optimize.minimize_scalar(lambda x: -norm.pdf(x, p[0], p[1]) / norm.pdf(x, q[0], q[1]),bounds=trunc)['x'] OptimizeResultRepresents the optimization result.
OptimizeWarning
The minimize function supports the following methods:
minimize(method=’Nelder-Mead’)
minimize(method=’Powell’)
minimize(method=’CG’)
minimize(method=’BFGS’)
minimize(method=’Newton-CG’)
minimize(method=’L-BFGS-B’)
minimize(method=’TNC’)
minimize(method=’COBYLA’)
minimize(method=’SLSQP’)
minimize(method=’dogleg’)
minimize(method=’trust-ncg’)
The minimize_scalar function supports the following methods:
minimize_scalar(method=’brent’)
minimize_scalar(method=’bounded’)
minimize_scalar(method=’golden’)
求函数最大/最小值的示例1
首先定义一个在区间(p[0], p[1])上要求最大值点x的函数norm.pdf(x, p[0], p[1])
Note: 要求最大值前面加一个-号就可以了,好像只有求最小值点的函数
加上求值区间
optimize.fminbound(lambda x: -norm.pdf(x, p[0], p[1]) / norm.pdf(x, q[0], q[1]), trunc[0], trunc[1])代入原来的函数中就可以求出最大值y了
[Mathematical optimization: finding minima of functions]
示例2
找到函数f(x,y)的最小值的,并且绘制出f所表示的曲面和寻找最小值时的搜索路径。f(x, y) = (1-x)^2+100(y-x^2)^2
f(x,y)对变量x和y的偏导函数为:
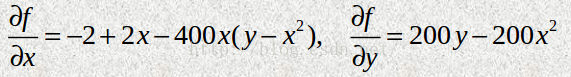
这个函数叫做Rosenbrock(罗森布罗克)函数,它经常用来测试最小化算法的收敛速度。它有一个十分平坦的山谷区域,收敛到此山谷区域比较容易,但是在山谷区域搜索到最小点则比较困难。根据函数的计算公式不难看出此函数的最小值是0,在(1,1)处。
"""
使用fmin()计算函数最小值,并用matplotlib绘制搜索最小值的路径。
"“”
import scipy.optimize as opt
import numpy as np
import sys
points = []
def f(p):
x, y = p
z = (1-x)**2 + 100*(y-x**2)**2
points.append((x,y,z))
return z
def fprime(p):
x, y = p
dx = -2 + 2*x - 400*x*(y - x**2)
dy = 200*y - 200*x**2
return np.array([dx, dy])
init_point =(-2,-2)
try:
method = sys.argv[1]
except:
method = "fmin_bfgs”
fmin_func = opt.__dict__[method]
if method in ["fmin", "fmin_powell"]:
result = fmin_func(f, init_point) #参数为目标函数和初始值
elif method in ["fmin_cg", "fmin_bfgs", "fmin_l_bfgs_b", "fmin_tnc"]:
result = fmin_func(f, init_point, fprime) #参数为目标函数、初始值和导函数(导函数可选?)
elif method in ["fmin_cobyla"]:
result = fmin_func(f, init_point, [])
else:
print "fmin function not found"
sys.exit(0)
f()计算f(x,y)的函数值,为了记录下最小化过程中的计算轨迹,在f()中将每个计算过的 点都添加进全局列表points中。fprime()计算f(x,y)对两个自变量在p处的偏导函数的值。最小化的初值设置为(-2,2),此程序从optimize模块的__dict_字典中获得由命令行 参数指定的最小值函数。
示例3
通过求解卷积的逆运算演示fmin的功能,比较fmin, fmin_powell, fmin_cg, fmin_bfgs。
对于一个离散的线性时不变系统h, 如果它的输入是x,那么其输出y可以用x和h的卷积表示:y = x (*) h。已知系统的输入x和输出y,计算传递函数h;或已知系统的传递函数h和输出y,计算系统的输入x。这种运算称为反卷积运算。fmin计算反卷积,这种方法只能用在很小规模的数列之上,不过用来评价fmin函数的性能还是不错的。
import scipy.optimize as opt
import numpy as np
def test_fmin_convolve(fminfunc, x, h, y, yn, x0):
#x (*) h = y, (*)表示卷积,yn为在y的基础上添加一些干扰噪声的结果,x0为求解x的初始值
def convolve_func(h):
#计算yn - x (*) h 的power,fmin将通过计算使得此power最小
return np.sum((yn - np.convolve(x, h))**2)
# 调用fmin函数,以x0为初始值
h0 = fminfunc(convolve_func, x0)
print fminfunc.__name__
print “---------------------“
# 输出x (*) h0 和y 之间的相对误差
print "error of y:", np.sum((np.convolve(x, h0)-y)**2)/np.sum(y**2)
# 输出h0 和h 之间的相对误差
print "error of h:", np.sum((h0-h)**2)/np.sum(h**2)
print
def test_n(m, n, nscale):
"""
随机产生x, h, y, yn, x0等数列,调用各种fmin函数求解b
m为x的长度, n为h的长度, nscale为干扰的强度
""“
x = np.random.rand(m)
h = np.random.rand(n)
y = np.convolve(x, h)
yn = y + np.random.rand(len(y)) * nscale
x0 = np.random.rand(n)
test_fmin_convolve(opt.fmin, x, h, y, yn, x0)
test_fmin_convolve(opt.fmin_powell, x, h, y, yn, x0)
test_fmin_convolve(opt.fmin_cg, x, h, y, yn, x0)
test_fmin_convolve(opt.fmin_bfgs, x, h, y, yn, x0)
if __name__ == "__main__":
test_n(200, 20, 0.1)
程序的输出:
fmin
---------------------
error of y: 0.00223334655127
error of h: 0.0883631777326
fmin_powell
---------------------
error of y: 0.000121416075668
error of h: 0.000191138253652
fmin_cg
---------------------
error of y: 0.000121010258418
error of h: 0.000191002626186
fmin_bfgs
---------------------
error of y: 0.000121010214197
error of h: 0.000191001784589
皮皮blog
非线性方程组求解
optimize模块中的fsolve()可以对非线性方程组进行求解,它的基本调用形式:fsolve(func, x0)参数:func是计算方程组误差的函数,func自己的参数x是一个数组,其值为方程组的一组可能的解,func返问将x代入方程组之后得到的毎个方程的误差。
x0为未知数的一组初始值。
假设要对下面的方程组进行求解:
f1(u1,u2,u3)=0, f2(u1,u2,u3)=0,f3(u1,u2,u3)=0
那么func可以如下定义:
def func(x):
u1,u2,u3 = x
return [f1(u1,u2,u3), f2(u1,u2,u3), f3(u1,u2,u3)]
示例
使用folve求非线性方程组的解,方程如下:(scipy_fsolve.py)from scipy.optimize import fsolve
from math import sin
def f(x):
x0, x1, x2 = x.tolist()
return [5*x1+3, 4*x0*x0 - 2*sin(x1*x2), x1*x2-1.5]
# f计算方程组的误差,[1,1,1]是未知数的初始值
result = fsolve(f, [1,1,1])
print result
print f(result)
输出为:
[-0.70622057 -0.6 -2.5 ]
[0.0, -9.1260332624187868e-14, 5.3290705182007514e-15]
Note: 由于fsolve函数在调用函数f时,传递的参数为数组,因此如果直接使用数组中的元素计算的话,计算速度将会有所降低,因此这里先用float函数将数组中的元素转换为Python中的标准浮点数,然后调用标准math库中的函数进行运算。
使用雅可比行列式求非线性方程组的解
雅可比矩阵jacobian雅可比矩阵是一阶偏导数以一定方式排列的矩阵,它给出了可微分方程与给定点的最优线性逼近,因此类似于多元函数的导数。例如前面的函数f1,f2,f3和未知数u1,u2,u3的雅可比矩阵如下:
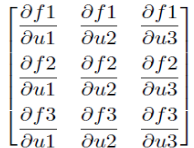
在对 方程组进行求解时,fsolve会自动计算方程组的雅可比矩阵,如果方程组中的未知数很多,而与每个方程有关的未知数较少时,即雅可比矩阵比较稀疏时,传递一个计算雅可比矩阵的函数将能大幅度提高运算速度。在一个模拟计算的程序中需要大量求解近有50个未知数的非线性方程组的解。每个方程平均与6个未知数相关,通过传递雅可比矩阵的计算函数使计算速度提高了4倍。
计算雅可比矩阵的函数j()和f()一样,其x参数是未知数的一组值,它计算非线性方程组在x处的雅可比矩阵。通过fprime参数将j()传递给fsolve()。
使用雅可比行列式求非线性方程组的解:
from scipy.optimize import fsolve
from math import sin,cos
def j(x):
x0, x1, x2 = x.tolist()
return [[0, 5, 0],
[8*x0, -2*x2*cos(x1*x2), -2*x1*cos(x1*x2)],
[0, x2, x1]]
result = fsolve(f, [1,1,1], fprime=j)
print result
print f(result)
Note: 由于本例中的未知数很少, 因此计算雅可比矩阵并不能显著地提高计算速度。
皮皮blog
其它使用实例
绘制温度限
定义函数来描述最小和最大温度。提示:这个函数以一年为周期。提示:包括时间偏移。对数据使用这个函数scipy.optimize.curve_fit()
绘制结果。是否拟合合理?如果不合理,为什么?
拟合精度的最大最小温度的时间偏移是否一样?
f(x,y) = (4 - 2.1x^2 + \frac{x^4}{3})x^2 + xy + (4y^2 - 4)y^2
变量应该限制在-2 < x < 2 , -1 < y < 1.
使用numpy.meshgrid()和plt.imshow来可视地搜寻区域。
使用scipy.optimize.fmin_bfgs()或其它多维极小化器。
然后绘制它。
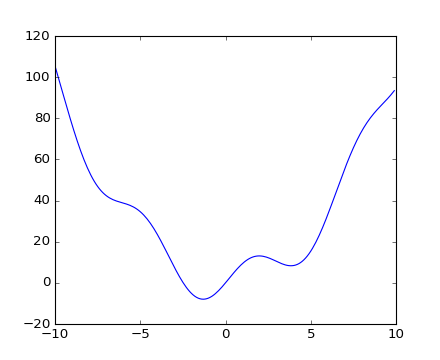
该函数在大约-1.3有个全局最小值,在3.8有个局部最小值。
关于不同最(极)小化方法的讨论
找到这个函数最小值一般而有效的方法是从初始点使用梯度下降法。BFGS算法是做这个的好方法:这个方法一个可能的问题在于,如果函数有局部最小值,算法会因初始点不同找到这些局部最小而不是全局最小.如果我们不知道全局最小值的邻近值来选定初始点,我们需要借助于耗费资源些的全局优化。为了找到全局最小点,最简单的算法是蛮力算法,该算法求出给定格点的每个函数值。对于大点的格点,scipy.optimize.brute()变得非常慢。
scipy.optimize.anneal()提供了使用模拟退火的替代函数。对已知的不同类别全局优化问题存在更有效率的算法,但这已经超出scipy的范围。一些有用全局优化软件包是 OpenOpt、 IPOPT、 PyGMO和 PyEvolve。
为了找到局部最小,我们把变量限制在(0, 10)之间,使用scipy.optimize.fminbound()
Note:在高级章节部分数学优化:找到函数最小值中有关于寻找函数最小值更详细的讨论。
找到标量函数的根
为了寻找根,例如令f(x)=0的点,对以上的用来示例的函数f我们可以使用scipy.optimize.fsolve()
注意仅仅一个根被找到。检查f的图像在-2.5附近有第二个根。我们可以通过调整我们的初始猜测找到这一确切值:
曲线拟合
假设我们有从被噪声污染的f中抽样到的数据:
如果我们知道函数形式(当前情况是x^2 + sin(x)),但是不知道幅度。我们可以通过最小二乘拟合拟合来找到幅度。首先我们定义一个用来拟合的函数:
然后我们可以使用scipy.optimize.curve_fit()来找到a和b:
现在我们找到了f的最小值和根并且对它使用了曲线拟合。我们将一切放在一个单独的图像中:
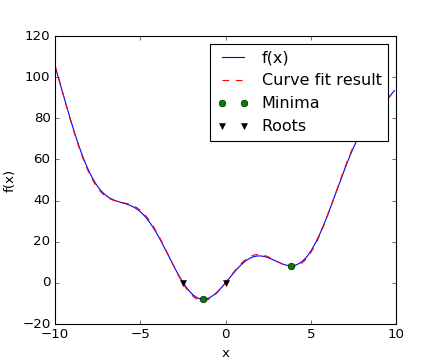
注意:Scipy>=0.11中提供所有最小化和根寻找算法的统一接口scipy.optimize.minimize(),scipy.optimize.minimize_scalar()和scipy.optimize.root()。它们允许通过method关键字方便地比较不同算法。
你可以在scipy.optimize中找到用来解决多维问题的相同功能的算法。
练习:曲线拟合温度数据
在阿拉斯加每个月的温度上下限,从一月开始,以摄氏单位给出。
练习:2维最小化
source code
[非线性最小二乘拟合:在点抽取地形激光雷达数据上的应用]
[Scipy:高端科学计算]
from: http://blog.csdn.net/pipisorry/article/details/51106570
ref: Optimization (scipy.optimize)
tutorial/optimize




