【星球两点距离】——最短距离计算理论和代码实现

背景

三体中有宇宙的坐标（三维空间坐标），使用欧氏距离计算即可；但具体到每个星球（球形）上的两点坐标（经纬度坐标系）的距离计算则不能使用欧氏距离，因为这是具有物理实际含义的工程距离计算问题，无法穿过地下到达目标点，所以只能像蚂蚁一样绕着球面行进到目标点，我称之为“蚂蚁找食物问题”，因为蚂蚁肯定是想法设法以最短的路径找到食物（目标点），所以这里也就符合本博客的任务，最短距离的计算（使用遗传算法、蚁群算法也是可以的，但这里是得到两点坐标后计算精确值，即解析法）。

理论介绍

地球表面两地之间的最短距离是通过这两点的大圆的劣弧段；
大圆：以地心为球心，以星球半径R为圆半径的圆

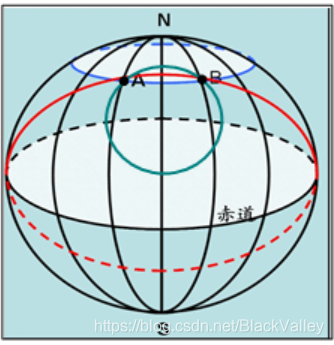
过AB两点线段最短，如果是圆弧，则是R越大圆弧越短，所以AB最短实际距离是过AB的大圆的劣弧长。

1、大圆有三个（类）：赤道、经线圈、晨昏线。3
2、如果两点的经度相差不大（在3°以内），可近似看作在同一经线上，最短距离＝纬差×111KM；如果两点的纬度相差不大（在3°以内），可近似看作在同一纬线上，最短距离＝经差×COS纬度×111KM。

1、若两点在赤道上，则两点间最短航线应是沿着赤道朝两点间的劣弧方向运动，即向东或向西。

2、若两点在同一条经线上，则两点间最短航线应是沿着经线朝两点间的劣弧方向运动，即向北或向南。

3、若两地的经度差等于180，则经过这两点大圆是经线圈。这两点间的最短距离是经过极点。

①同在北半球，最短航线必须经过北极点，其航行方向一定是先向正北，过北极点后再向正南。②同在南半球，最短航线必须经过南极点，其航行方向一定是先向正南，过南极点后再向正北。③两地位于不同半球，这时需要考虑经过北极点为劣弧，还是经过南极点为劣弧，然后确定最短航线的走向和航程。

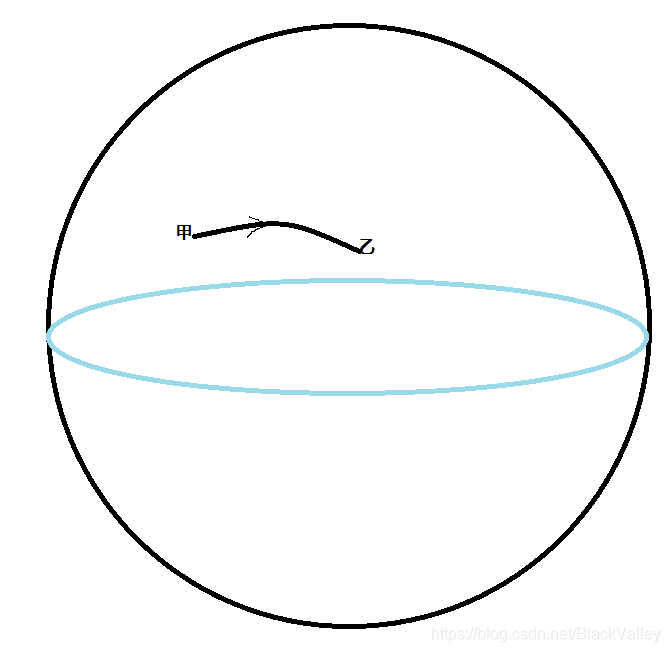
4、若两地的经度差不等于180，则经过这两点大圆不是经线圈，而是与经线圈斜交，其最短航线不经过极点：
从甲到乙，北半球，先西北再西南 / 先东北再东南 比较距离较短者。

编程实现

依据为：

$\widehat{AB}=Rarccos(cos(W_A)cos(W_B)cos(J_B-J_A)+sin(W_A)sin(W_B))$
经纬度都化成弧度单位

'''
计算地球两点距离
'''
from math import *R = 6371393  # 6371.393kmdef distance(jA, wA, jB, wB):# 角度转换为弧度jA, wA, jB, wB = jA / 180 * pi, wA / 180 * pi, jB / 180 * pi, wB / 180 * pireturn R * acos(cos(wA) * cos(wB) * cos(jB - jA) + sin(wA) * sin(wB))

参考

CSDN博客1
CSDN博客2