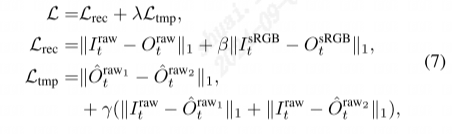Video Modeling with Correlation Networks 阅读

本文主要是介绍Video Modeling with Correlation Networks 阅读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文阅读之前，建议先简要看一遍 FlowNet 和 R(2+1)D

一.论文背景及方法

1.背景

motion是识别视频中动作的重要线索，当前的动作识别模型一般使用两种方法：

1. 通过光流的输入，来显式的运用时间信息，或者说是运动信息，比如著名的two-stream网络
2. 通过使用能够同时获取时间和外观信息的3D 卷积filter来进行操作

第一种方式的缺陷有

• 不是完全end-to-end的视频分析，需要离线计算光流，计算光流比较耗时，没法达到实时
• 解决的是short-term 视频分析，没法有效的解决long-term 视频分析

第二种方式的缺陷是3D卷积网络的参数更多，更难训练。

但是以上两种方法均有缺陷，故本文提出一种新方法，替代方法是可学习的相关算子（learnable correlation operator）。

2.方法

本文的相关网络包含有可学习的相关算子（learnable correlation operator），其作用是在不同网络层的卷积feature map建立相关关系（此处指的是相邻的卷积特征），在得到时间信息的同时，与一般的二维卷积得到的特征相结合，最终在四个动作识别基准（Kinetics, Something-Something, Diving48 and Sports1M）上表现出色，论文中提供一种思路：将可学习的相关算子与其他算子一起使用，建立新的体系结构，以达到SOTA结果。

与3D卷积相比，将外观和运动的计算分解，并学习不同的filter，以获取不同的patch的相似性，在视频建模方面更具有优势。
与two-stream网络相比，也可以显示地运用时间信息，但训练速度更快，two-stream网络只在后期进行时空的融合，本论文所提出的可以在整个网络中集成外观和时间信息。

二.相关算子(Correlation Operator)

1.不可学习的相关算子

这是一种基本的相关算子。出自FLowNet，但在FLowNet中，相关算子是不可学习的，并且仅使用了一次。下面直接用公式说明计算过程

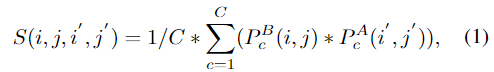
结合上面的图1a，对此计算方式作简要介绍，首先将image A和imageB 看作两个三维的tensor，大小为$C\ast H\ast W$ , imageB中的一个patch为 $P^B(i,j)$, imageA中的一个patch为$P^A(i^{\prime }，j^{\prime })$,为了便于计算，将每个patch缩小到一个像素，然后按照对应通道进行相乘，将所有乘积加起来，再除C（目的是标准化），就得到了其中的一个数值。$(i^{\prime }，j^{\prime })$是被限制在$(i，j)$的 K * K邻域，图1a中所示，K=3。最后的输出S的大小为$K\ast K\ast H\ast W$, K * K被作为通道，可以看成$K^2\ast H\ast W$.

2.可学习的相关算子

原始的相关算子不包括可学习的参数，因此就其可生成的表示类型而言，是相当有限的。因此在其中加入一个可学习的filter，如图1（b）所示。动机是学习在匹配过程中选择信息通道。为了实现这一目标，在点积计算公式1中引入了权重向量:$W_c\ast P_c^B（i，j）\ast P_c^A（i^{\prime }，j^{\prime }）$。
K表示匹配两个patch时的最大位移,较大的K值可以覆盖较大的区域并获得更多的信息，不利的一面是，计算成本呈K²增长。在此可以使用膨胀卷积，例如，用一个膨胀因子D=2来设置K=7，以覆盖13×13像素的区域。

3.分组的相关算子

相关算子将特征从 C * H* W 转换为 K² * H* W。在流行的 cnn 中，C可以大于 K²的一到两个数量级,这意味着相关算子可能会导致通道维数的大幅度减少。本文想要设计一个基于相关算子的网络并重复应用，它将显著降低通道的维数，并降低学习特征的表示能力，这是非常不利的。
因此本文采用了分组的相关算子，如图1（c）所示，在保持效率的同时减少了通道数量，借鉴于分组卷积，利用这一思想，将所有通道分成G个组，就相当于每组g=C/G，在每组内分别计算，最后所有组的输出叠加在一起，输出的大小为$G\ast K\ast K\ast H\ast W$,通道数为K²G。

4.从视频clip角度看相关算子

将其应用于视频分类，其中输入是一个L个的视频帧序列。通过计算输入序列中每对相邻帧的相关性，将该算子扩展到视频。因为相邻帧对的数量是L− 1，除了相邻帧对的相关外，还额外计算第一帧的自相关，如图1（d）所示。

相关算子目的是捕获相邻帧之间的信息。相关算子为视频分类提供了一种建模时间信息的方法，比流行的3D卷积具有更少的参数和FLOPs，如表1所示。

三.相关网络

上文提到，相关算子是提供建模时间信息的方法，因此他必须和其他能够捕获外观信息的operator结合起来使用，本文使用R(2+1)D作为backbone。
R(2+1)D是将3D卷积转变为2D的空间卷积和1D的时间卷积，具体来说，原来是（3* 3* 3），现在将其转变为（1* 3* 3）和（3* 1* 1）

在A Closer Look at Spatiotemporal Convolutions for Action Recognition论文中说明，原来是N_i 个N_i−1 ×t ×d ×d 的3D卷积，转变为M_i个N_i−1 ×1 ×d ×d 的2D空间卷积和N_i个M_i×t ×1 ×1的1D时间卷积，其中M_i的计算方式为

这样选择出来的M_i，使得（2+1）D中的参数数量大约等于全3D卷积的参数数量。
将相关算子加入到R(2+1)D，在此，提出两种类型的模块
第一种是correlation-sum，设计思路与bottleneck block类似，在开始和结束都加入1×1×1 大小的卷积，并且使用残差连接。第二种是correlation-concat，在块内有两个分支: 一个分支带有相关算子，另一个分支通过1 × 1 × 1的卷积，最后两个分支的输出通过通道维度结合在一起，具体如图所示

最后，将该模块插入R(2+1)D中得到最终的网络结构，在表2的res2、res3和res4之后插入一个模块，res5忽略不用

四.小结

• 提出了一种可学习的相关算子，利用膨胀和分组，计算效率高
• 将相关算子加入到R（2+1）D中，集成运动和外观信息
• 在不采用光流的情况下，达到了SOTA的表现

这篇关于Video Modeling with Correlation Networks 阅读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---