本文主要是介绍每日OJ题_简单多问题dp⑧_力扣188. 买卖股票的最佳时机 IV,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
力扣188. 买卖股票的最佳时机 IV
状态机分析
解析代码
力扣188. 买卖股票的最佳时机 IV
188. 买卖股票的最佳时机 IV
难度 困难
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
1 <= k <= 1001 <= prices.length <= 10000 <= prices[i] <= 1000
class Solution {const int INF = 0x3f3f3f3f;
public:int maxProfit(int k, vector<int>& prices) {}
};状态机分析
这题和力扣123. 买卖股票的最佳时机 III一样,因为这题用的解题思路是适配这题的,所以把上一题的最多交易两次换成最多交易k次即可,思路基本力扣123一样,看了力扣123可跳过:
以某个位置为结尾,结合题目要求,定义一个状态表示: 由于有买入和卖出(可交易)两个状态,因此可以选择用两个数组。但是这道题里面还有交易次数的限制,因此还需要再加上一维,用来表示交易次数。其中:
- f[i][j] 表示:第 i 天结束后,完成了 j 次交易,处于买入状态,此时的最大利润,
- g[i][j] 表示:第 i 天结束后,完成了 j 次交易,处于卖出(可交易)状态,此时的最大利润。
状态机:
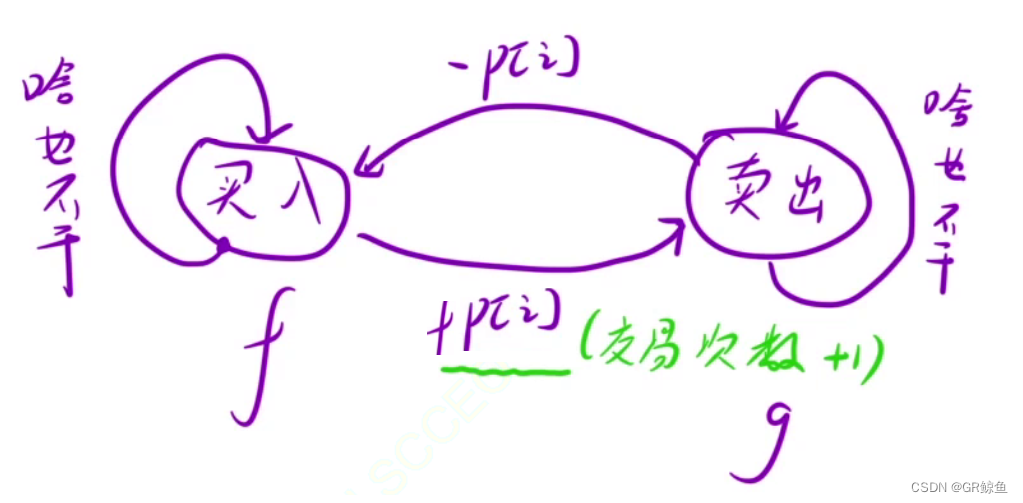
状态转移方程:
对于 f[i][j] ,有两种情况到这个状态:
- 在 i - 1 天的时候,交易了 j 次,处于买入状态,第 i 天啥也不干即可。此时最大利润为: f[i - 1][j] ;
- 在 i - 1 天的时候,交易了 j 次,处于卖出(可交易)状态,第 i 天的时候把股票买了。此时的最大利润为: g[i - 1][j] - prices[i] 。
综上,要的是最大利润,因此是两者的最大值: f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]) ;
对于 g[i][j] ,也有两种情况可以到达这个状态:
- 在 i - 1 天的时候,交易了 j 次,处于卖出(可交易)状态,第 i 天啥也不干即可。此时的最大利润为: g[i - 1][j] ;
- 在 i - 1 天的时候,交易了 j - 1 次,处于买入状态,第 i 天把股票卖了,然后就完成了 j 比交易。此时的最大利润为: f[i - 1][j - 1] + prices[i] 。但是这个状态不⼀定存在,要先判断⼀下。
综上,我们要的是最大利润,因此状态转移方程为:
g[i][j] = g[i - 1][j];
if(j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
初始化、填表顺序、返回值:
对于 f 表由于需要用到 i = 0 时的状态,因此初始化第一行即可。 当处于第 0 天的时候,只能处于买入过一次的状态,此时的收益为 -prices[0] ,因此 f[0][0] = - prices[0] ,其它为负无穷。
对于 g 表由于需要用到 i = 0 时的状态,因此初始化第一行即可。 当处于第 0 天的时候,处于卖出(可交易)状态,啥也不干即可,此时的收益为0 ,因此 f[0][0] = 0,其它为负无穷。
对于负无穷:为了取 max 的时候,⼀些不存在的状态起不到干扰的作用,将它们初始化为负INF (用INT_MIN 在计算过程中会有溢出的风险,这里 INF 折半取 0x3f3f3f3f ,足够小即可)。
填表顺序从左往右两个表一起填,最后返回 g 表最后一行的最大值。
解析代码
class Solution {const int INF = 0x3f3f3f3f;
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();k = min(k, n / 2); // 小优化,交易次数不大于天数的一半vector<vector<int>> f(n, vector<int>(k+1, -INF));vector<vector<int>> g(n, vector<int>(k+1, -INF));f[0][0] = -prices[0];g[0][0] = 0;for(int i = 1; i < n; ++i){for(int j = 0; j <= k; ++j){f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i]);g[i][j] = g[i-1][j];if(j-1 >= 0)g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i]);}}int ret = 0;for(int i = 0; i <= k; ++i){ret = max(ret, g[n-1][i]);}return ret;}
};这篇关于每日OJ题_简单多问题dp⑧_力扣188. 买卖股票的最佳时机 IV的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







