牛客练习赛46----E-华华和奕奕学物理

本文主要是介绍牛客练习赛46----E-华华和奕奕学物理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

首先发出题目链接：
链接：https://ac.nowcoder.com/acm/contest/894/E
来源：牛客网
涉及：树状数组

题目如下：
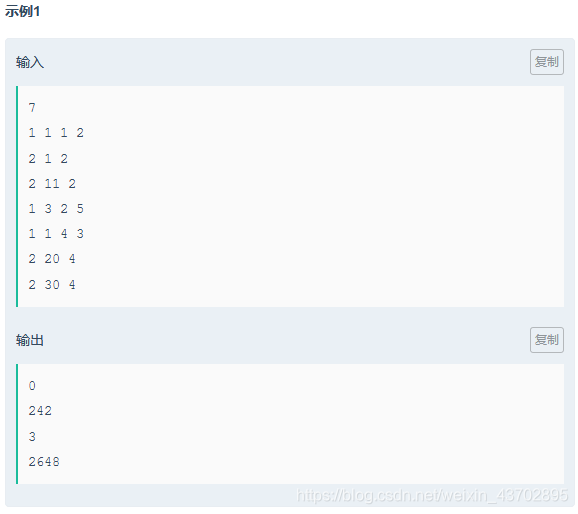
在这里插入图片描述
此题目有两个变量，时间t和初速度v。由于某一时刻小球a的速度比小球b的速度快，那么在任何时间小球a的速度都比小球b的速度快。

由于每一个小球拥有不同的初速度，以及抛出的时间也不同，为了更好的判断两个小球的速度关系，我们可以通过比较两个小球在t=maxt=3e5时的速度，来间接比较两个小球的速度关系。

对于某一次抛球（op=1），输入m,v,t，可以得到此球在maxt=3e5时的速度V=v+g*(maxt-t)；
对于某一次询问（op=2），输入v,t，可以求出V=v+g*(maxt-t)，那么所询问的球都是当t=3e5时速度小于V的球。

问题在于，如何知道t=3e5时刻速度小于V有哪些球，可以利用树状数组来存某一些重要的值。

对于某一个在t₁时刻，初速度为v，质量为m的球，那么t₂时刻此球的动能ans为 $\frac{1}{2}m(v+(t_{2}-t_{1})g)^{2}$
2*ans为： $m(v+(t_{2}-t_{1})g)^{2}$
展开可得： $m(v^{2}-2gvt_{1}+t_{1}^{2}g^{2})+mt_{2}(2gv-2t_{1}g^{2})+mt_{2}g^{2}$
此球在maxt时的速度 $V = v + (m a x t - t) * g$
令A= $m(v^{2}-2gvt_{1}+t_{1}^{2}g^{2})$ ，B= $m(2gv-2t_{1}g^{2})$ ，C= $mg^{2}$

则对于任意在t时刻抛出，质量为m，初速度为v的球，此球在t₂时刻的2*ans为：
$A+Bt_{2}+Ct_{2}^{2}$
对于一系列在t₁，t₂…t_n时刻，质量为m₁，m₂…m_n，初速度为v₁，v₂…v_n的所有球，在t₀时刻的2*ans之和为
$A_{1}+A_{2}+...+A_{n})+(B_{1}+B_{2}+...+B_{n})t_{0}+(C_{1}+C_{2}+...+C_{n})t_{0}^{2}$

由此，可以以每一个球在maxt的速度V为主键，将每一个的A,B,C三个值分别存放在三个树状数组（tree）里面（树状数组介绍可以看这个博客）

const ll maxn=4e6;//这里maxn代表V的最大可能值，V=v+g*(t2-t1),但是maxn比V的最大值还要大。
const ll maxt=3e5+5;
ll tree[4][maxn]={0};

即对于每次抛球（op=1）,输入v,t,m，求出V=v+(maxt-t)，然后定点修改树状数组tree[0,1,2][V]

void add(ll tr[],int V,ll mv){for(int i=V;i<=maxn-2;i+=lowerbit(i))tr[i]=(tr[i]+mv)%mod;
}

if(op==1){scanf("%lld%lld%lld",&v,&t,&m);int V=v+(maxt-t)*g;add(tree[0],V,m*(v*v%mod-2*g*v*t%mod+t*t%mod*g%mod*g%mod)%mod);add(tree[1],V,m*(2*g*v%mod-2*t%mod*g%mod*g%mod)%mod);add(tree[2],V,m*g*g%mod);}

对于每次查询（op=2），输入v,t，先求出V=v+(maxt-t)，然后求和

ll sum(ll tr[],int V){ll ans=0;for(int i=V;i>0;i-=lowerbit(i))ans+=tr[i];return ans;
}

if(op==2){scanf("%d%d",&v,&t);int V=v+(maxt-t)*g;//在t=3e5时候，此球的速度ll sumv=0;sumv=(sumv+sum(tree[0],V))%mod;sumv=(sumv+sum(tree[1],V)*t%mod)%mod;sumv=(sumv+sum(tree[2],V)*t%mod*t%mod)%mod;printf("%lld\n",(sumv+mod)%mod);}

代码如下：

#include <iostream>
using namespace std;
typedef long long ll;
const ll maxn=4e6;
const ll maxt=3e5+5;
const ll g=10;
const ll mod=1e9+7;
ll tree[4][maxn]={0};
ll q,v,t,m;
int op;
int lowerbit(int x){//lowerbit函数return x&-x;
}
void add(ll tr[],int V,ll mv){//树状数组之单点修改for(int i=V;i<=maxn-2;i+=lowerbit(i))tr[i]=(tr[i]+mv)%mod;
}
ll sum(ll tr[],int V){//树状数组之区间查询ll ans=0;for(int i=V;i>0;i-=lowerbit(i))ans+=tr[i];return ans;
}
int main(){scanf("%lld",&q);while(q--){scanf("%d",&op);if(op==1){scanf("%lld%lld%lld",&v,&t,&m);int V=v+(maxt-t)*g;//在t=3e5时候，此球的速度，由此来判断单点修改的位置//下面三个树状数组用来存上面所说A,B,C的值add(tree[0],V,m*(v*v%mod-2*g*v*t%mod+t*t%mod*g%mod*g%mod)%mod);add(tree[1],V,m*(2*g*v%mod-2*t%mod*g%mod*g%mod)%mod);add(tree[2],V,m*g*g%mod);}else{scanf("%d%d",&v,&t);int V=v+(maxt-t)*g;//判断区间求和的位置ll sumv=0;//下面求多项式(A1+A2+A3+...)+(B1+B2+B3+...)*t+(C1+C2+C3+...)*t*t的值//即求动能之和sumv=(sumv+sum(tree[0],V))%mod;sumv=(sumv+sum(tree[1],V)*t%mod)%mod;sumv=(sumv+sum(tree[2],V)*t%mod*t%mod)%mod;printf("%lld\n",(sumv+mod)%mod);}}return 0;
}