【牛客练习赛46-A】华华教奕奕写几何【二分】

题目大意：

题目链接：https://ac.nowcoder.com/acm/contest/894/A

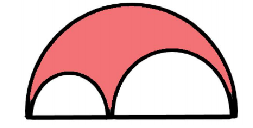
给出红色部分面积，求大圆的最短直径（两小圆直径之和等于大圆直径）。

思路：

$orzWYC,XYYdalao$反正我是没有看出开个根号就好了。
先把问题转化为圆中的问题。

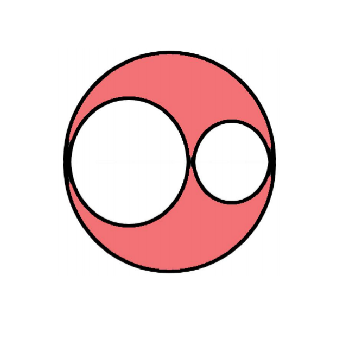
此时红色部分面积就为$2s$了。而所有圆的直径不变。
设两个小圆的直径分别为$x,y$，大圆的直径为$m$，我们欲求
$$\pi x^2+\pi y^2=\pi m^2-2s$$
移项得
$$2s=\pi m^2-\pi x^2-\pi y^2$$

$$2s=\pi (m^2-x^2-y^2)$$

$$\frac{2s}{\pi }=m^2-x^2-y^2$$

等号左边是已知的。由于要求大圆的直径最小，所以可以考虑二分$m$。
有一点很显然的是，当两小圆直径差$|x-y|$越大，两小圆面积之和$\pi x^2+\pi y^2$越大。
所以这也是满足单调性的。可以考虑二分$x$来验证直径为$m$时是否合法。
$pi$保留小数点后15位。一开始保留7位被卡精度了。。。
时间复杂度$O({\log }^2(maxlen))$

代码：

#include <cstdio>
#include <cmath>
using namespace std;const double pi=3.141592653589793;
const double minn=0.00001;
double s;bool check(double x)
{double l=0.0,r=x,mid,sum;while (r-l>=minn){mid=(l+r)/2.0;sum=mid*mid+(x-mid)*(x-mid)+s;if (sum>x*x) r=mid;else l=mid;}if (x/2.0-r<=minn) return 0;return 1;
}int main()
{scanf("%lf",&s);s=s*2.0/pi;double l=0.0,r=2000000.0,mid;while (r-l>=minn){mid=(l+r)/2.0;if (check(mid)) l=mid;else r=mid;}printf("%0.3lf",l);return 0;
}