本文主要是介绍python统计分析——单变量分布之量化变异度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考资料:python统计分析【托马斯】
1、极差
极差仅仅是最高值和最低值之间的差异。使用函数为:numpy.ptp()。代码如下:
import numpy as npx=np.arange(1,11)
np.ptp(x)ptp代表“峰值到峰值”,唯一应该注意的异常值,即数据点的值比其他数据高或低很多。通常,这些点是由于样本选择或测量过程中的错误引起的。
有许多检查异常值的测试。其中之一检查那些高于第三分位数1.5×四分位距(IQR)或低于第一分位数1.5×四分位距(IQR)的数据。
2、百分位数
弄懂百分位数的最简单方法,就是首先定义累计分布函数(CDF):
CDF是PDF(概率密度函数)从负无穷大到给定值的积分,因此确定了低于该值的数据的百分比。了解了CDF之后,计算在a~b范围内知道值x的可能性就简单了:在a和b之间找到值得概率可由该范围内PDF的积分得到,并且可以通过相应的CDF值的差来得到:
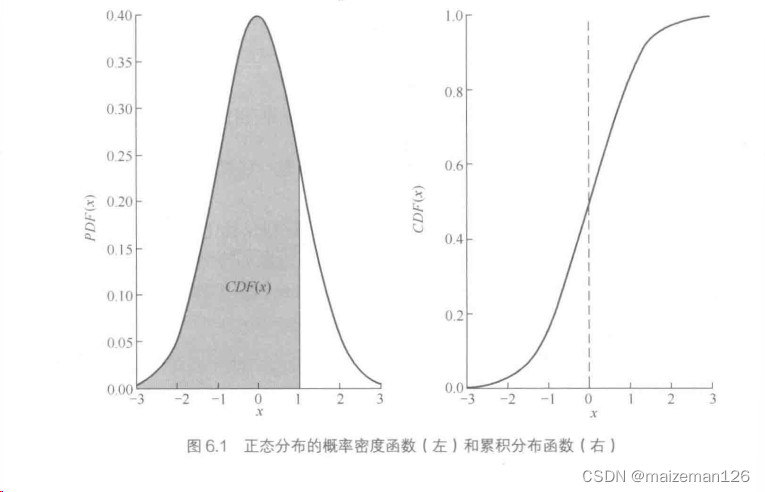
对于离散分布来说,积分就由求和代替。
回到百分位数:这些只是CDF的逆函数,其给出低于数据中特定百分比的数据的值。虽然“百分位数”这个表达并不常常出现,但经常会遇到特定的百分位数。如下:
①为了获得包含95%的数据范围,我们必须找到 样本分布的2.5分位数和97.5分位数。
②50分位数就是中位数。
③另一个重要的就是四分位数,即25和75分位数。它们之间的差值称为四分位距(IQR).
3、标准差和方差
样本方差的极大似然估计如下:
但上式系统性地低估了总体方差,因此本称为总体方差的“有偏估计”。换句话说,如果你选择了特定总体标准差的人群,并且重复1000次从该人群中选择n个随机样本,并计算每个样本的标准偏差,则这些样本标准差的平均值将低于总体表标准差。
我们总是使用样本均值,使得给定的样本数据方差最小化,从而低估了总体的方差。所以群体方差的最佳无偏估计应该是:
本式即为样本方差。
标准差是方差的平方根,样本标准差是样本方差的平方根:
在统计学中通常用σ表示总体标准差,用s表示样本标准差。
python标准差函数为:numpy.std(),方差函数为:numpy.var();参数设置可参考:python统计分析——单变量描述统计-CSDN博客
代码操作如下:
data=np.arange(7,14)
# numpy默认用n还计算方差和标准差,即ddof=0。
# 为了能够得到样本方差和标准差,须设置ddof=1
np.std(data,ddof=1)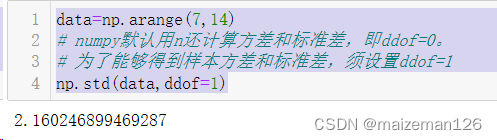
4、标准误
标准误是系数标准差的估计。对于正态分布的数据,均值的样本标准误差(SE或SEM)是:
5、置信区间
在数据的统计分析中,经常估计参数的置信区间。α%的置信区间(CI)表示包含参数的真实值的范围,其可能性为α%。
如果采样分布式对称的和单峰的(也就是说,在最大值的两边平滑地衰减),通常可以用下面公式来估计置信区间:
其中,std为标准差,N_PPF是标准正态分布分布的百分点函数(PPF)。要计算95%的双侧置信区间,须计算标准正态分布分布的PPF(0.025),来得到置信区间的上下限。
注①:计算平均值的置信区间,标准差必须用标准误代替。
注②:如果分布是偏斜的,上面的公式就不再适用。
这篇关于python统计分析——单变量分布之量化变异度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




