[ARC120E]1D Party

本文主要是介绍[ARC120E]1D Party，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1D Party

题解

我们可以将原来的序列随时间变化转化成一个图像，纵轴代表时间，横轴代表$A$的值。

那么我们可以得到这样一个图像：

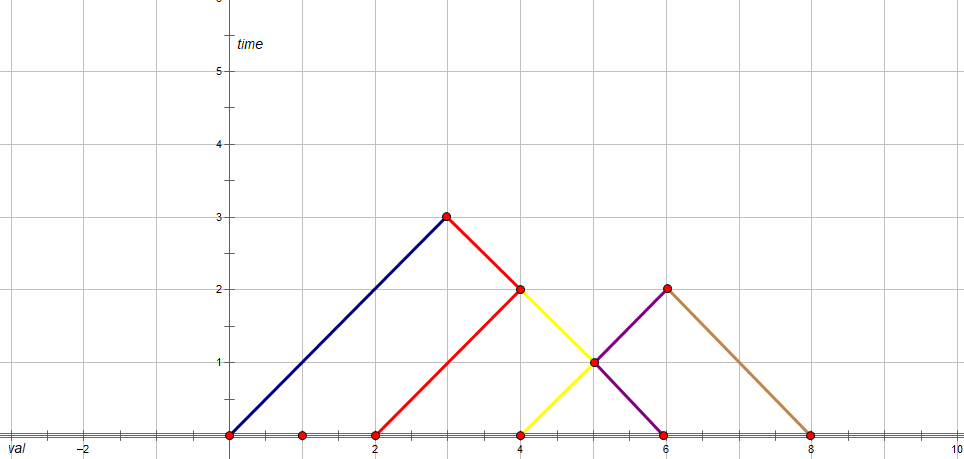
其中不同颜色代表不同的点的运动路径。

由于要最优，我们肯定要让每个点都一直处于运动状态，我们发现每个点大概有一下两种运动状态：

• 先向左走直到与另一个点相遇，再一直向右走。
• 先向右走直到与另一个点相遇，再一直向左走。

无论如何，与别的点相遇时都一定会产生一个交点，然后拐弯。

我们可以考虑每个点都不拐弯，而是交换它们的目标对象，也就是$i$与$i+1$第一次相遇后就让$i$去与$i+2$相遇，$i+1$与$i-1$去相遇。

这样我们的图像可以被转化成这个样子：

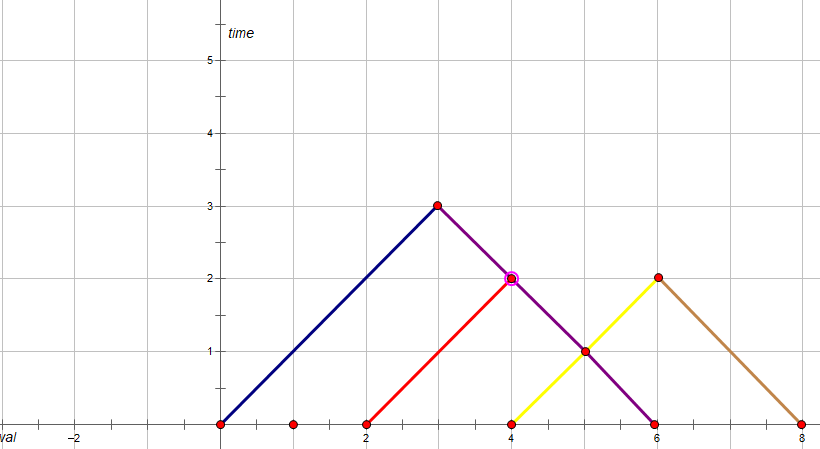
我们相当于得到了无数个三角形连接而成的连通块，当这些三角形所有三角形都联通的时候所有点都是满足条件的。

而我们的答案相当于最高的三角形的最高的高度。

于是我们就很容易想到通过$dp$去找到这个值，设$d{p}_i$表示前$i$个都满足条件的最小高度。

容易得到转移方程式：
$$d{p}_i=\underset{j=1}{\overset{i-2}{\min }}(max(d{p}_j,\frac{a_i}{2}$$

这篇关于[ARC120E]1D Party的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---