本文主要是介绍【DL经典回顾】激活函数大汇总(十三)(Sinc SwiGLU附代码和详细公式),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
激活函数大汇总(十三)(Sinc & SwiGLU附代码和详细公式)
更多激活函数见激活函数大汇总列表
一、引言
欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或缺的角色,它们决定着神经元的输出,并且影响着网络的学习能力与表现力。鉴于激活函数的重要性和多样性,我们将通过几篇文章的形式,本篇详细介绍两种激活函数,旨在帮助读者深入了解各种激活函数的特点、应用场景及其对模型性能的影响。
在接下来的文章中,我们将逐一探讨各种激活函数,从经典到最新的研究成果。
限于笔者水平,对于本博客存在的纰漏和错误,欢迎大家留言指正,我将不断更新。
二、Sinc
Sinc激活函数是一种在信号处理中广泛使用的函数,近年来也被探索用于深度学习模型中。它基于数学中的sinc函数,特别是在处理时间序列数据和频率分析时显示出其独特优势。
1. 数学定义
Sinc激活函数通常定义为:
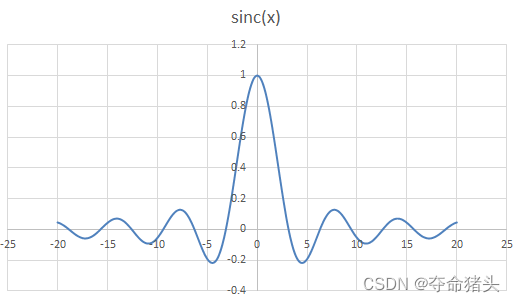
Sinc ( x ) = { 1 if x = 0 sin ( π x ) π x otherwise \operatorname{Sinc}(x)= \begin{cases}1 & \text { if } x=0 \\ \frac{\sin (\pi x)}{\pi x} & \text { otherwise }\end{cases} Sinc(x)={1πxsin(πx) if x=0 otherwise
这里, x x x是激活函数的输入。
2. 函数特性
- 振荡和衰减:Sinc函数在 x = 0 x=0 x=0处取得最大值1,并随着 x = 0 x=0 x=0离开原点而振荡衰减。这种特性使得Sinc函数能够捕捉到数据中的周期性和频率信息。
- 带宽选择:Sinc函数的形状和衰减速度与信号的带宽选择密切相关,这在处理有限带宽信号时非常重要。
- 非局部性:与大多数激活函数相比,Sinc函数对输入的变化更加敏感,即使是远离原点的输入变化也能影响输出。
3. 导数
Sinc函数的导数是:
d d x Sinc ( x ) = { 0 if x = 0 π x cos ( π x ) − sin ( π x ) ( π x ) 2 otherwise \frac{d}{d x} \operatorname{Sinc}(x)= \begin{cases}0 & \text { if } x=0 \\ \frac{\pi x \cos (\pi x)-\sin (\pi x)}{(\pi x)^2} & \text { otherwise }\end{cases} dxdSinc(x)={0(πx)2πxcos(πx)−sin(πx) if x=0 otherwise
导数在 x = 0 x=0 x=0处是连续的,尽管看起来像是未定义。通过洛必达法则,可以证明当 x = 0 x=0 x=0时,导数为0。
4. 使用场景与局限性
使用场景:
- 信号处理:在需要进行频率分析和带宽处理的信号处理应用中,Sinc激活函数能够有效地捕捉信号的周期性和频率特征。
- 时间序列分析:在分析和预测周期性时间序列数据时,Sinc激活函数可以帮助模型更好地理解数据的频率信息。
局限性:
- 梯度消失:由于Sinc函数远离原点时的振荡衰减,梯度可能变得非常小,导致梯度消失问题。
- 计算复杂性:Sinc函数涉及三角函数计算,相比于ReLU等简单激活函数,其计算成本更高。
5.代码实现
import numpy as npdef sinc_activation(x):"""计算Sinc激活函数的值。参数:x -- 输入值,可以是数值、NumPy数组或者多维数组。返回:Sinc激活后的结果。"""# 处理x=0的情况,以避免除以0的错误x_pi = np.pi * xresult = np.where(x == 0, 1, np.sin(x_pi) / x_pi)return result
解读
- 处理除以零的情况:
np.where(x == 0, 1, np.sin(x_pi) / x_pi)这行代码首先检查x是否等于0。对于等于0的情况,直接返回1,这是因为根据Sinc函数的定义,当(x=0)时,函数值为1。 - Sinc函数计算:对于非零的输入值,函数计算
np.sin(x_pi) / x_pi,其中x_pi是输入x乘以π。这实现了Sinc函数的标准定义: Sinc ( x ) = sin ( π x ) π x \operatorname{Sinc}(x)=\frac{\sin (\pi x)}{\pi x} Sinc(x)=πxsin(πx)。 - 向量化操作:这个实现利用了NumPy的向量化操作能力,允许函数直接作用于整个数组,无需显式循环。这对于在深度学习模型中高效处理大量数据至关重要。
示例使用
# 创建一个从-10到10的数组
x = np.linspace(-10, 10, 100)
# 计算Sinc激活值
y = sinc_activation(x)# 使用Matplotlib绘制结果
import matplotlib.pyplot as pltplt.plot(x, y)
plt.title("Sinc Activation Function")
plt.xlabel("x")
plt.ylabel("Sinc(x)")
plt.grid(True)
plt.show()
这段代码演示了如何计算一系列输入值的Sinc激活,并使用Matplotlib绘制了Sinc函数的图像。
三、SwiGLU
SwiGLU (Swish Gated Linear Unit) 激活函数是深度学习中的一种激活函数,结合了Swish激活函数和GLU (Gated Linear Unit) 的特性。SwiGLU 旨在利用Swish的平滑非饱和性质和GLU的动态门控能力,提高模型在处理复杂数据时的表现力。尽管“SwiGLU”并非广泛认知的标准术语,这里的介绍基于其构成元素的理论基础。
1. 数学定义
考虑到SwiGLU的概念是基于Swish和GLU的结合,它的定义可能类似于:
SwiGLU ( a , b ) = Swish ( a ) ⊙ σ ( b ) \operatorname{SwiGLU}(a, b)=\operatorname{Swish}(a) \odot \sigma(b) SwiGLU(a,b)=Swish(a)⊙σ(b)
其中:
- a a a和 b b b是相同维度的输入向量。
- Swish ( a ) = a ⋅ σ ( a ) \operatorname{Swish}(a)=a \cdot \sigma(a) Swish(a)=a⋅σ(a), σ ( a ) = 1 1 + e − a \sigma(a)=\frac{1}{1+e^{-a}} σ(a)=1+e−a1是Sigmoid函数。
- ⊙ \odot ⊙表示元素乘法。
- σ ( b ) \sigma(b) σ(b) 是对输入(b)应用Sigmoid激活函数。
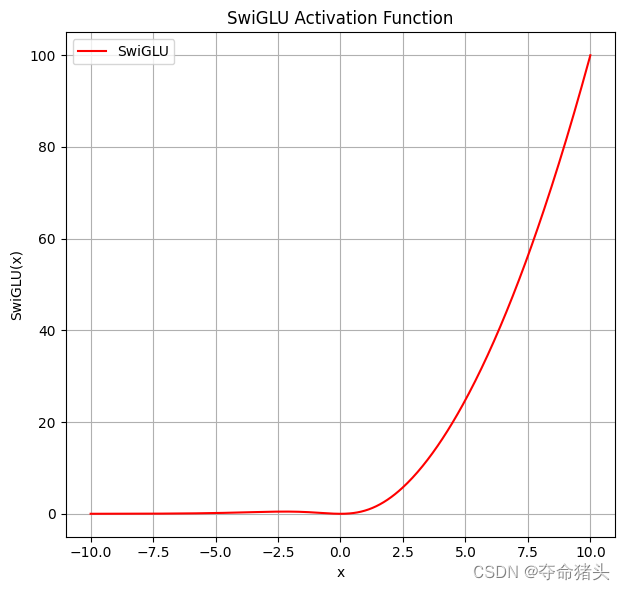
2. 函数特性
- 自适应门控机制:通过 σ ( b ) \sigma(b) σ(b)为 a a a的Swish激活提供动态门控,使模型可以根据数据自适应地调整信息流。
- 平滑激活:结合Swish激活函数的平滑性,SwiGLU既能捕获深层网络中的复杂特征,又能保持较好的梯度流动。
- 增强的非线性和表现力:通过Swish和门控机制的结合,SwiGLU能够为深度学习模型提供强大的非线性表现力。
3. 导数
SwiGLU的导数结合了Swish函数和Sigmoid门控的导数,具体表达式较为复杂,需要通过链式法则计算。
4. 使用场景与局限性
使用场景:
- 复杂数据建模:在需要模型理解和处理具有复杂结构和关系的数据时,如自然语言处理(NLP)和图像识别。
- 深度网络:在构建深层网络模型时,SwiGLU的非饱和特性和门控机制有助于缓解梯度消失问题,提升训练效果。
局限性:
- 计算开销:SwiGLU的计算相比简单的激活函数更为复杂,可能增加模型的训练时间和资源消耗。
- 优化难度:高度非线性和动态门控机制可能使得模型参数的优化变得更加困难,需要细致的调参和足够的训练数据。
5.代码实现
import numpy as npdef sigmoid(x):return 1 / (1 + np.exp(-x))def swish(x):return x * sigmoid(x)def swiglu(a, b):"""参数:a -- 输入值,可以是数值、NumPy数组或者多维数组。b -- 用于门控的输入,维度应与a相同。返回:根据SwiGLU激活机制处理后的结果。"""return swish(a) * sigmoid(b)
解读
- Swish激活:
swish(a)对输入(a)应用Swish激活函数,这部分是通过输入(a)和它的Sigmoid激活值相乘来实现的,有助于引入非线性并保持梯度流动良好。 - Sigmoid门控:
sigmoid(b)为输入(b)应用Sigmoid函数,生成一个介于0和1之间的门控信号。这个信号决定了经过Swish激活的(a)有多少信息可以流过。 - 元素乘法:最终通过将
swish(a)的结果和sigmoid(b)的结果相乘,实现了SwiGLU激活。这样,(a)的每个元素都会根据(b)中对应元素的门控信号被调节。
示例使用
# 示例输入
a = np.array([0.5, -1, 2, -2])
b = np.array([1, -1, 0, 2])# 应用SwiGLU激活函数
output = swiglu(a, b)print("SwiGLU Output:", output)
这个例子展示了如何对两组输入a和b应用SwiGLU激活函数。
四、参考文献
- Oppenheim, A. V., & Schafer, R. W. (1975). “Digital Signal Processing.” Prentice-Hall. 这本书详细介绍了数字信号处理的基本概念,包括Sinc函数的使用和其在信号重建中的重要性。
这篇关于【DL经典回顾】激活函数大汇总(十三)(Sinc SwiGLU附代码和详细公式)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






