ConvE——二维卷积知识图谱横空出世

《Convolutional 2D Knowledge Graph Embeddings》论文理解+代码复现

本论文理解不再翻译原文，只写上我对于论文原生态的理解，应该会比较详细，请读者放心。

一.作者为什么要提出ConvE？

传统的R-GCN和DistMult的参数量过大，并且模型深度不够深，只能处理较小的知识图谱，所以作者将CNN引入到图神经网络中。

二.一维卷积与二维卷积的对比

2.1一维卷积

当a,b特征简单一维concat时,使用的是一维卷积横向滑动：

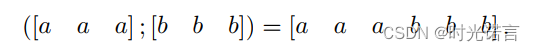
但是这样有一个弊端，其实一维卷积不能提取出来很多a和b之间的关系（即a和b交界的位置），因此横向移动的意义变得十分微小。

2.2二维卷积

作者想到在构造特征时就使用2D的方式（即使用二维的拼接方式），这样便可以方便使用二维卷积来更好地提取a和b各自以及交互的特征。

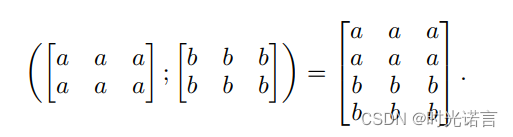
特别的（如下图），当a，b特征交互排列时，二维卷积的作用将会更大：

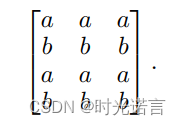
三.目标

在链接预测任务中，分为编码部分和评分部分。

编码部分的工作是将每个实体（如人、地点或事物）和关系（如“位于”或“朋友”）从知识图谱中映射到向量空间中的嵌入。

评分部分则根据事实三元组中的实体和关系的嵌入来计算分数。分数反映了一个给定的事实三元组（例如，一对实体和它们之间的关系）为真的可能性。

训练中的参数更新主要就是这两部分。

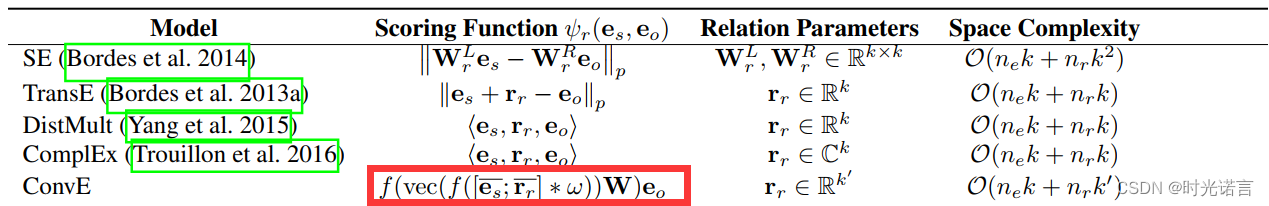
现在我们只看ConvE的评分函数（如上图红色框）

• f：一个非线性函数，比如ReLU激活函数。
• vec：将矩阵展平成向量的操作。
• [es​;r]：实体嵌入 es和关系嵌入 r 的拼接。
• ∗ω：与卷积核ω 进行卷积操作。
• W：权重矩阵，用于在卷积后将特征映射到目标空间。
• eo：目标实体的嵌入。

整个表达式的含义是：首先将源实体嵌入和关系嵌入进行拼接，然后与卷积核做卷积操作，并应用非线性函数。之后，将结果展平成向量，与权重矩阵 W 相乘，最后与目标实体嵌入eo的内积，得到预测的评分。这个评分反映了给定三元组作为真实事实的可能性。

此外，该训练的过程最后的损失函数是二元交叉熵损失函数。

四.评分函数详细解释

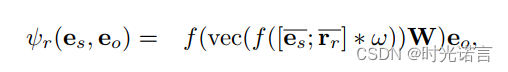
以上是完整的评分函数定义。

下面是流程



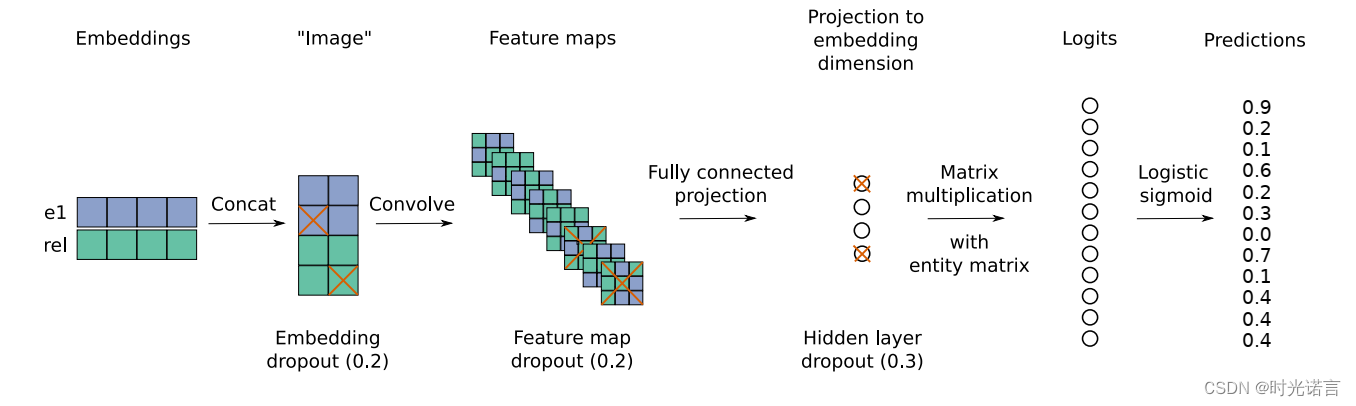
计算速度的提升就在于1-N Scoring的提出，那为什么ConvE可以同时对多个尾部实体进行预测呢？下面是答案：

五.实验部分与结论

5.1实验部分

在对比实验部分，作者主要将ConvE与DistMult作为比较。
可以看出，在相同参数量时，ConvE的性能就已经超过DistMult了，当然随着参数的增大，ConvE的性能并没有得到质的提升。

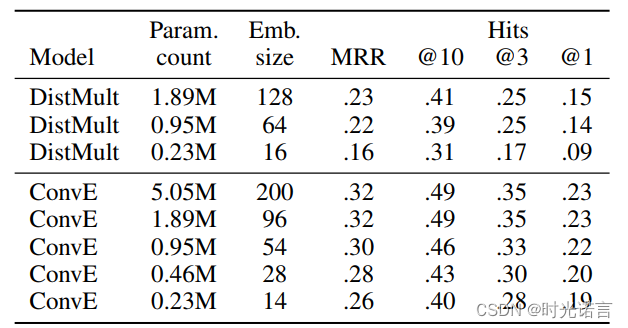
对于其他的超参设置, 作者在论文中指出, 大的卷积核效果不如多个小卷积核效果好(这点与CV中结论一致, 基本已经成常识了)。

在inverse model（如下图）检测部分，ConvE表现得非常良好。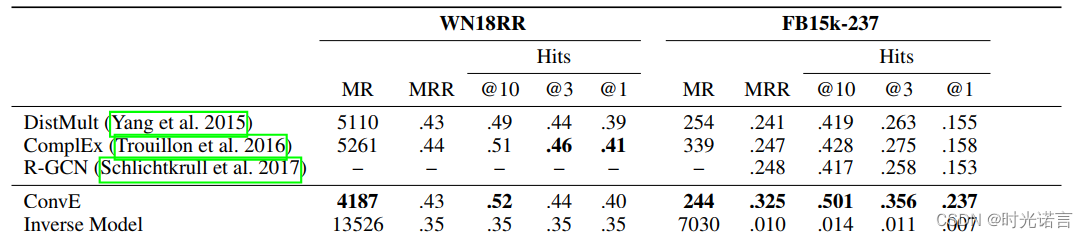

在消融实验部分（如下图），各种Dropout似乎对ConvE的影响很大, 1 - N Scoring的增益也不小, 标签平滑倒是不怎么重要

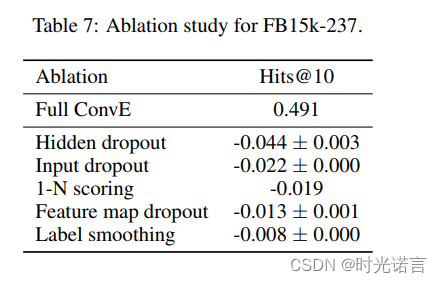
5.2结论与展望

作者引入了ConvE，一个使用2D卷积和多层非线性特征来建模知识图谱的链接预测模型。ConvE参数少，评分速度快，通过非线性特征的多层表示抵抗过拟合，并在多个数据集上取得了良好结果。此外，我们调查了WN18和FB15k数据集中通过逆关系泄露测试集的问题，并确保所有调查数据集都有健壮的版本。尽管ConvE与计算机视觉中的卷积架构相比还是较浅，但未来的工作可能会涉及更深层次的卷积模型，以及如何在嵌入空间强化大规模结构以增加交互。

六.代码复现

import torch
from torch.nn import functional as F,Parameter
from torch.autograd import Variable
from torch.nn.init import xavier_normal_,xavier_uniform_
from torch.nn.utils.rnn import pack_padded_sequence,pad_packed_sequence
class ConvE(torch.nn.Module):def __init__(self,args,num_entities,num_relations):"""Args:args (string*): 参数设置num_entities (int): 知识图谱中实体的数量num_relations (int): 知识图谱中关系的数量"""super(ConvE,self).__init__()self.emb_e=torch.nn.Embedding(num_entities,args.embedding_dim,padding_idx=0) #将单词转化为args.embedding_dim规定的向量self.emb_rel=torch.nn.Embedding(num_relations,args.embedding_dim,padding_idx=0)self.inp_drop=torch.nn.Dropout(args.input_drop)self.hidden_drop=torch.nn.Dropout(args.hidden_drop)self.feature_map_drop=torch.nn.Dropout2d(args.feature_drop)self.loss=torch.nn.BCELoss()self.emb_dim1=args.embedding_shape1#self.emb_dim1: 是重塑后矩阵的一个维度，它由模型的参数 args.embedding_shape1 直接给定self.emb_dim2=args.embedding_dim//self.emb_dim1#self.emb_dim2: 是计算得出的另一个维度，由嵌入向量的总维度 args.embedding_dim 除以 self.emb_dim1 得到self.conv1=torch.nn.Conv2d(1,32,(3,3),1,0,bias=args.use_bias)self.bn0=torch.nn.BatchNorm2d(1)self.bn1=torch.nn.BatchNorm2d(32)self.bn2=torch.nn.BatchNorm1d(args.embedding_dim)self.register_parameter('b',Parameter(torch.zeros(num_entities)))self.fc=torch.nn.Linear(args.hidden_size,args.embedding_dim)print(num_entities,num_relations)def init(self):xavier_normal_(self.emb_e.weight.data)xavier_normal_(self.emb_rel.weight.data)def forward(self,e1,rel):e1_embedded=self.emb_e(e1).view(-1,1,self.emb_dim1,self.emb_dim2)#reshaperel_embedded=self.emb_rel(rel).view(-1,1,self.emb_dim1,self.emb_dim2)#reshapestacked_inputs=torch.cat([e1_embedded,rel_embedded],2)stacked_inputs=self.bn0(stacked_inputs)x=self.inp_drop(stacked_inputs)x=self.conv1(x)x=self.bn1(x)#从1维升至32维x=F.relu(x)x=self.feature_map_drop(x)x=x.view(x.shape[0],-1)#除了第一个维度，其他展平x=self.fc(x)x=self.hidden_drop(x)x=self.bn2(x)x=F.relu(x)x=torch.mm(x,self.emb_e.weight.transpose(1,0)) #(batch_size,emb_size)×(emb_size,num_entities)=(batch_size,num_entities)x+=self.b.expand_as(x)pred=torch.sigmoid(x)return  pred  

以上代码只涉及ConvE的模型核心构建，并没有涉及其应用。还请点赞收藏为我助力催更hh