本文主要是介绍非线性表中的树、堆是干嘛用的 ?其数据结构是怎样的 ?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!


1. 前言
想学好前端,先练好内功,内功不行,就算招式练的再花哨,终究成不了高手。
非线性表(树、堆),可以说是前端程序员的内功,要知其然,知其所以然。
笔者写的 JavaScript 数据结构与算法之美 系列用的语言是 JavaScript ,旨在入门数据结构与算法和方便以后复习。
非线性表中的树、堆是干嘛用的 ?其数据结构是怎样的 ?
希望大家带着这两个问题阅读下文。
2. 树
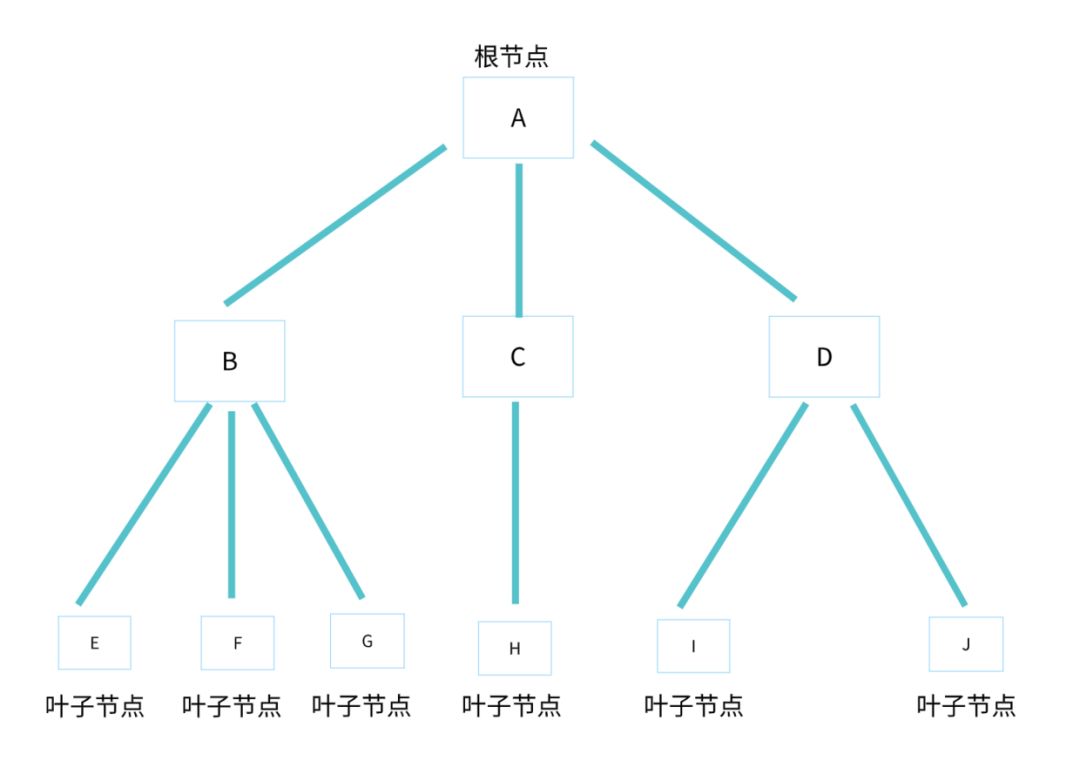
树的数据结构就像我们生活中的真实的树,只不过是倒过来的形状。
术语定义
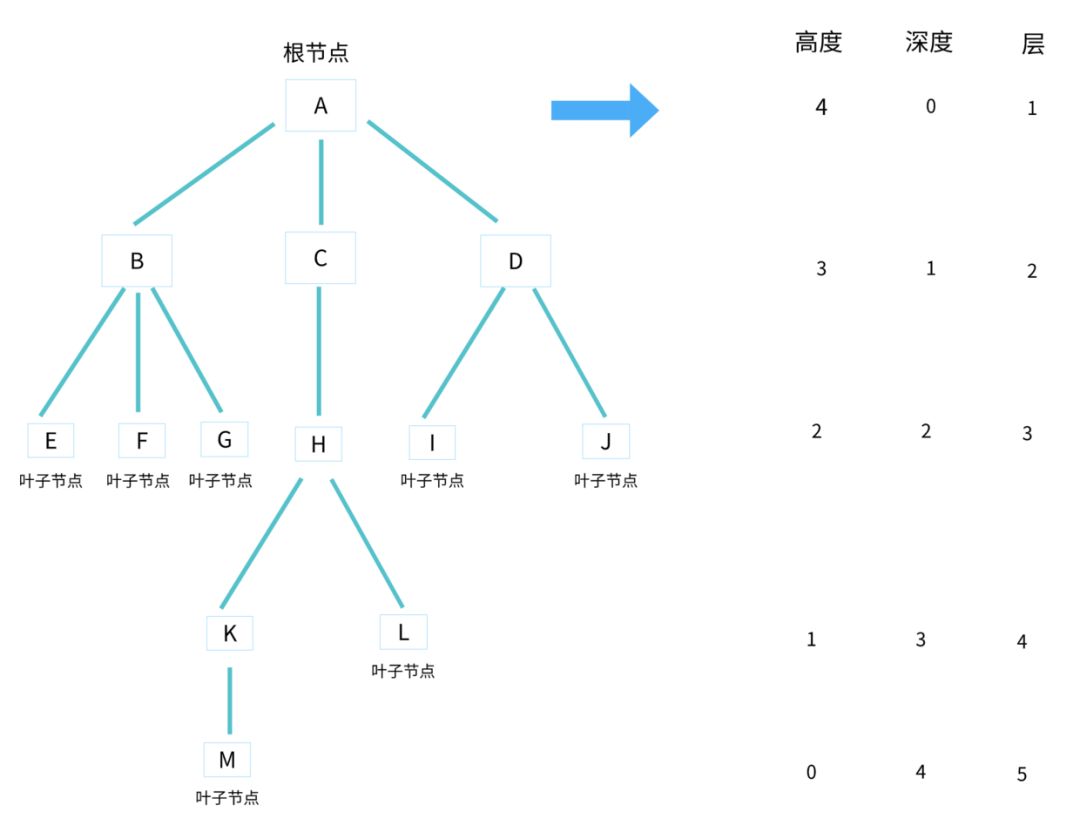
高度是从下往上度量,比如一个人的身高 180cm ,起点就是从 0 开始的。深度是从上往下度量,比如泳池的深度 180cm ,起点也是从 0 开始的。高度和深度是带有度字的,都是从 0 开始计数的。而层数的计算,是和我们平时的楼层的计算是一样的,最底下那层是第 1 层,是从 1 开始计数的,所以根节点位于第 1 层,其他子节点依次加 1。
二叉树分类
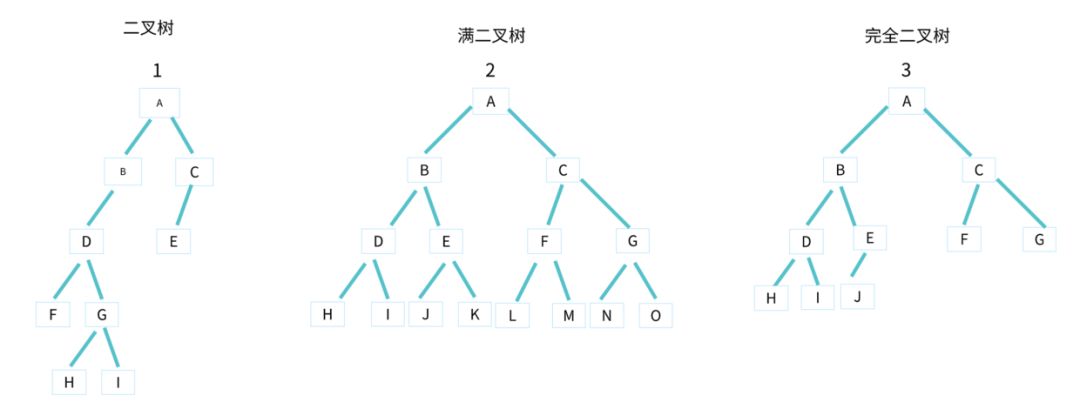
二叉树
满二叉树
完全二叉树
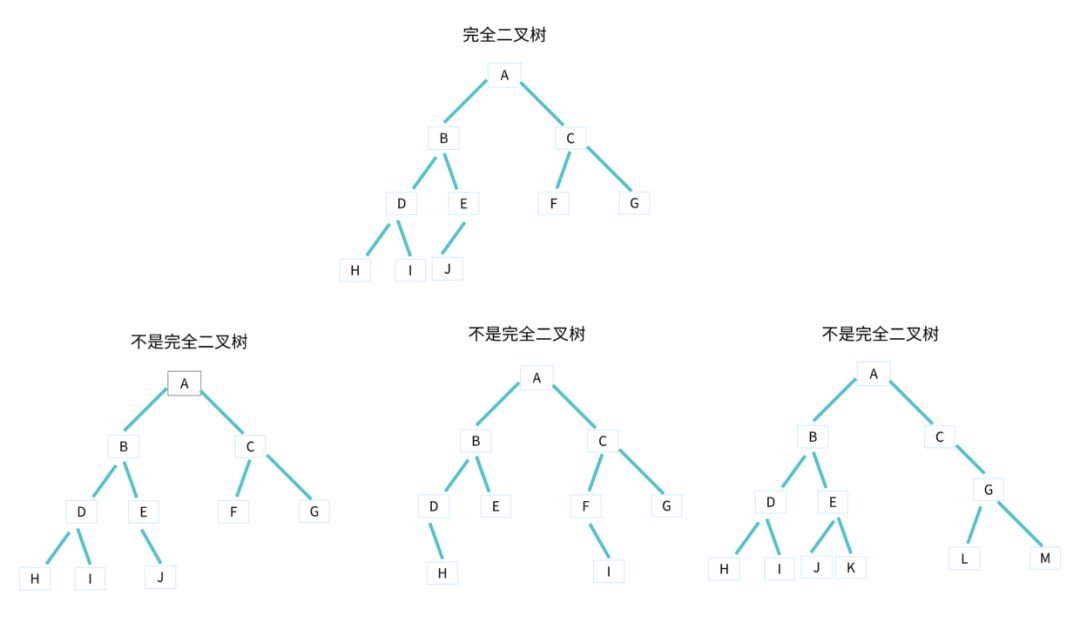
堆
之前的文章 栈内存与堆内存 、浅拷贝与深拷贝 中有说到:JavaScript 中的引用类型(如对象、数组、函数等)是保存在堆内存中的对象,值大小不固定,栈内存中存放的该对象的访问地址指向堆内存中的对象,JavaScript 不允许直接访问堆内存中的位置,因此操作对象时,实际操作对象的引用。
那么堆到底是什么呢 ?其数据结构又是怎样的呢 ?
堆其实是一种特殊的树。只要满足这两点,它就是一个堆。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作大顶堆。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作小顶堆。
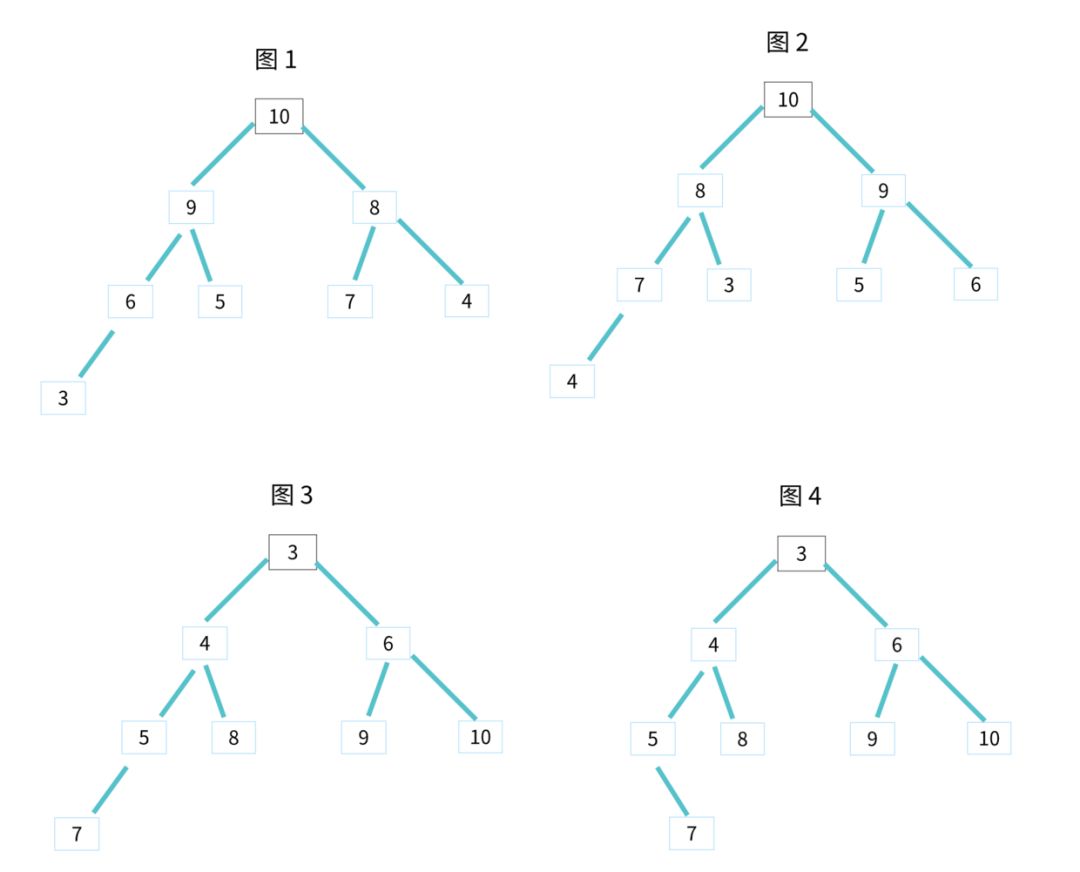
其中图 1 和 图 2 是大顶堆,图 3 是小顶堆,图 4 不是堆。除此之外,从图中还可以看出来,对于同一组数据,我们可以构建多种不同形态的堆。
二叉查找树(Binary Search Tree)
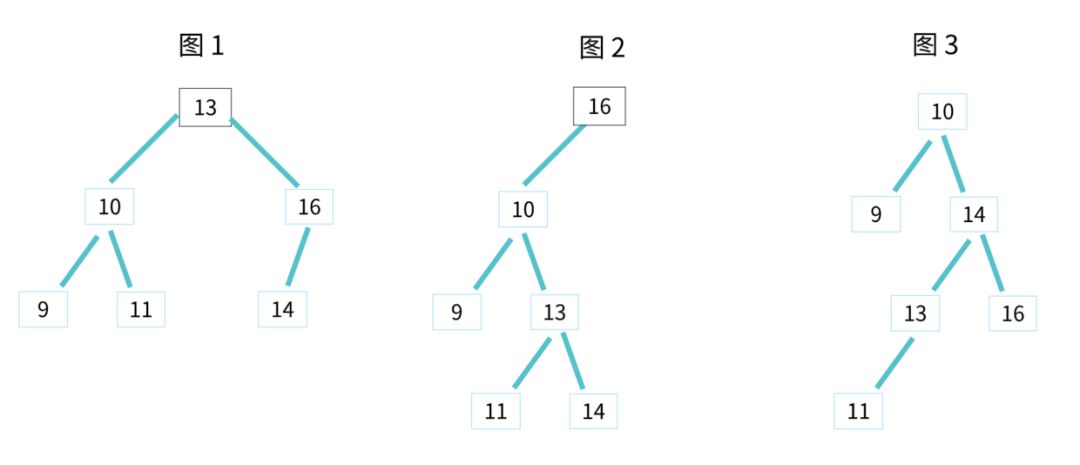
平衡二叉查找树
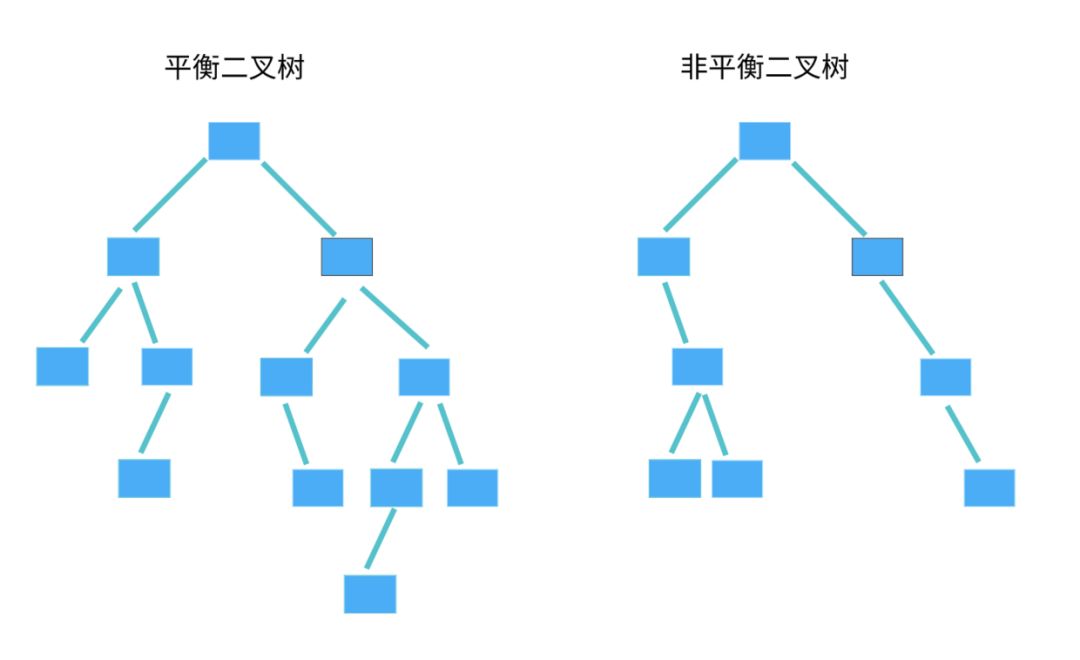
红黑树(Red-Black Tree)
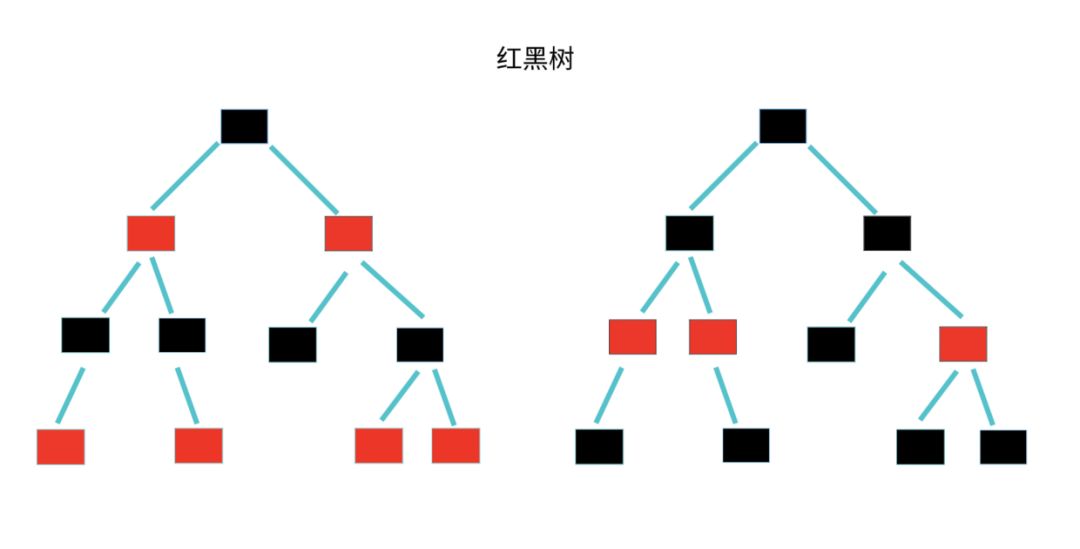
红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
下面两个都是红黑树。
存储
完全二叉树的存储
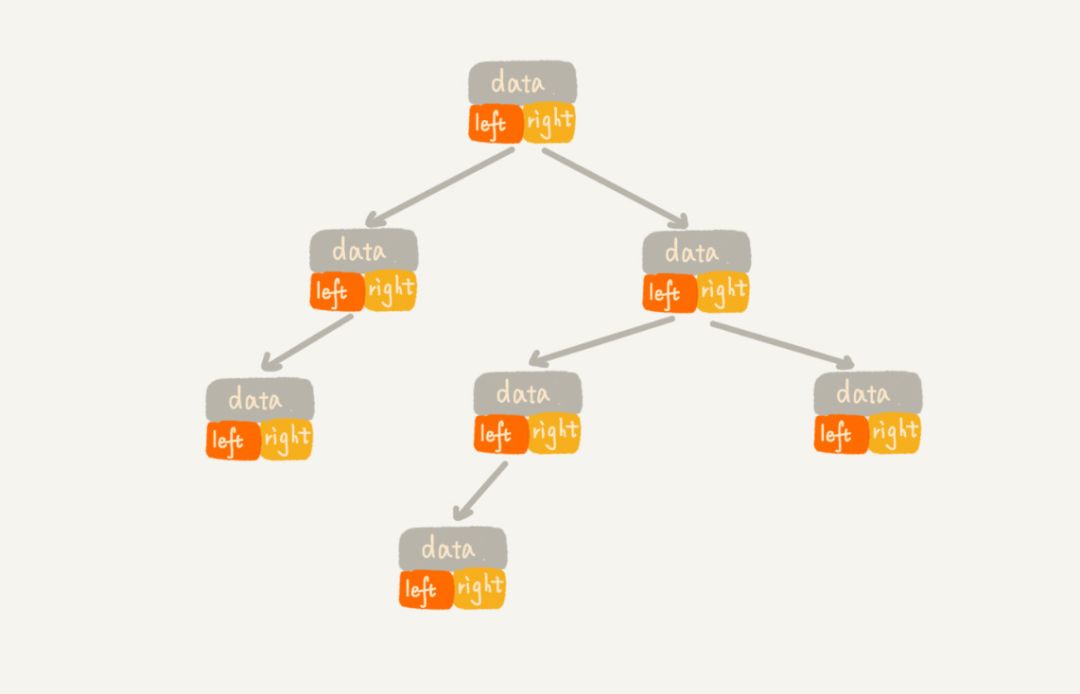
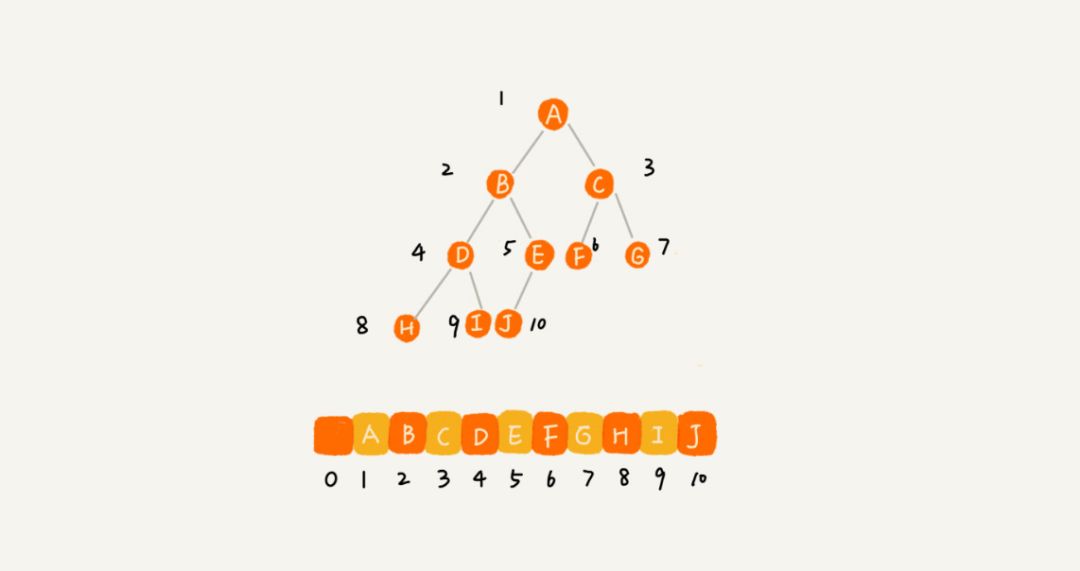
二叉树的遍历
经典的方法有三种:前序遍历、中序遍历、后序遍历。其中,前、中、后序,表示的是节点与它的左右子树节点遍历访问的先后顺序。
前序遍历(根 => 左 => 右)
中序遍历(左 => 根 => 右)
后序遍历(左 => 右 => 根)
实际上,二叉树的前、中、后序遍历就是一个递归的过程。
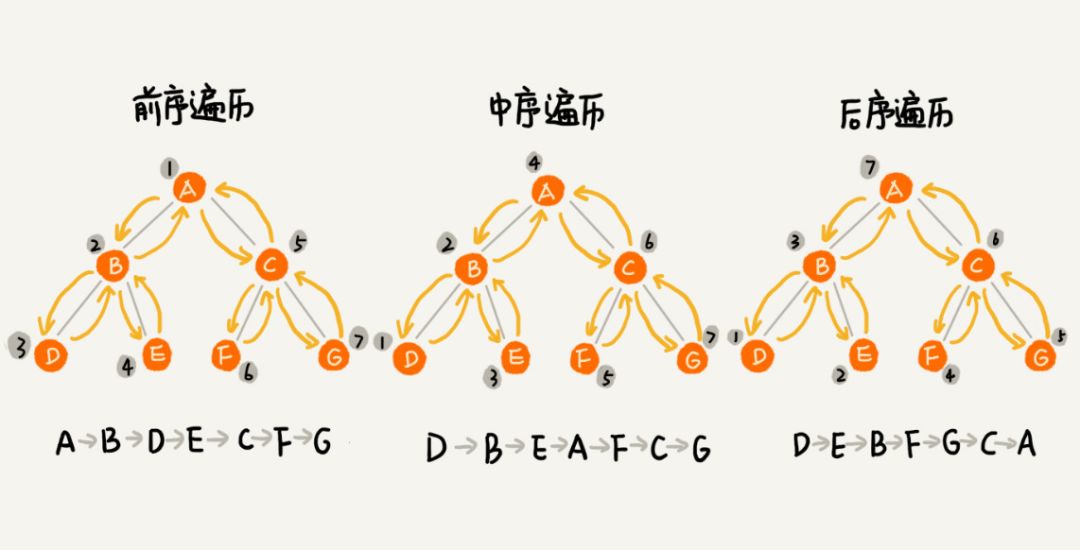
时间复杂度:3 种遍历方式中,每个节点最多会被访问 2 次,跟节点的个数 n 成正比,所以时间复杂度是 O(n)。
实现二叉查找树
二叉查找树的特点是:相对较小的值保存在左节点中,较大的值保存在右节点中。
代码实现二叉查找树,方法有以下这些。
方法
遍历
具体代码
// 二叉查找树类function BinarySearchTree() { // 用于实例化节点的类 var Node = function(key){ this.key = key; // 节点的健值 this.left = null; // 指向左节点的指针 this.right = null; // 指向右节点的指针 }; var root = null; // 将根节点置为null}
function BinarySearchTree() {
// 用于实例化节点的类
var Node = function(key){
this.key = key; // 节点的健值
this.left = null; // 指向左节点的指针
this.right = null; // 指向右节点的指针
};
var root = null; // 将根节点置为null
}
this.insert = function(key){ var newNode = new Node(key); // 实例化一个节点 if (root === null){ root = newNode; // 如果树为空,直接将该节点作为根节点 } else { insertNode(root,newNode); // 插入节点(传入根节点作为参数) }};// 插入节点的函数var insertNode = function(node, newNode){ // 如果插入节点的键值小于当前节点的键值 // (第一次执行insertNode函数时,当前节点就是根节点) if (newNode.key < node.key){ if (node.left === null){ // 如果当前节点的左子节点为空,就直接在该左子节点处插入 node.left = newNode; } else { // 如果左子节点不为空,需要继续执行insertNode函数, // 将要插入的节点与左子节点的后代继续比较,直到找到能够插入的位置 insertNode(node.left, newNode); } } else { // 如果插入节点的键值大于当前节点的键值 // 处理过程类似,只是insertNode函数继续比较的是右子节点 if (node.right === null){ node.right = newNode; } else { insertNode(node.right, newNode); } }}function(key){
var newNode = new Node(key); // 实例化一个节点
if (root === null){
root = newNode; // 如果树为空,直接将该节点作为根节点
} else {
insertNode(root,newNode); // 插入节点(传入根节点作为参数)
}
};
// 插入节点的函数
var insertNode = function(node, newNode){
// 如果插入节点的键值小于当前节点的键值
// (第一次执行insertNode函数时,当前节点就是根节点)
if (newNode.key < node.key){
if (node.left === null){
// 如果当前节点的左子节点为空,就直接在该左子节点处插入
node.left = newNode;
} else {
// 如果左子节点不为空,需要继续执行insertNode函数,
// 将要插入的节点与左子节点的后代继续比较,直到找到能够插入的位置
insertNode(node.left, newNode);
}
} else {
// 如果插入节点的键值大于当前节点的键值
// 处理过程类似,只是insertNode函数继续比较的是右子节点
if (node.right === null){
node.right = newNode;
} else {
insertNode(node.right, newNode);
}
}
}
在下图的树中插入健值为 6 的节点,过程如下:
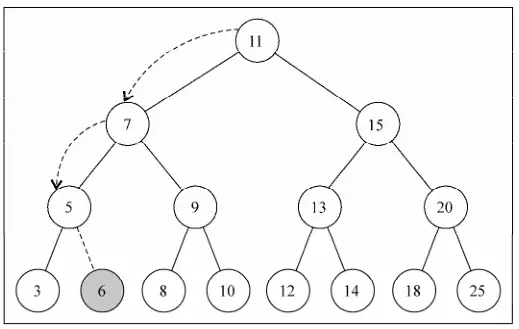
this.min = function(node) { // min方法允许传入子树 node = node || root; // 一直遍历左侧子节点,直到底部 while (node && node.left !== null) { node = node.left; } return node;};function(node) {
// min方法允许传入子树
node = node || root;
// 一直遍历左侧子节点,直到底部
while (node && node.left !== null) {
node = node.left;
}
return node;
};
this.max = function(node) { // min方法允许传入子树 node = node || root; // 一直遍历左侧子节点,直到底部 while (node && node.right !== null) { node = node.right; } return node;};function(node) {
// min方法允许传入子树
node = node || root;
// 一直遍历左侧子节点,直到底部
while (node && node.right !== null) {
node = node.right;
}
return node;
};
this.search = function(key, node){ // 同样的,search方法允许在子树中查找值 node = node || root; return searchNode(key, node);};var searchNode = function(key, node){ // 如果node是null,说明树中没有要查找的值,返回false if (node === null){ return false; } if (key < node.key){ // 如果要查找的值小于该节点,继续递归遍历其左侧节点 return searchNode(node.left, key); } else if (key > node.key){ // 如果要查找的值大于该节点,继续递归遍历其右侧节点 return searchNode(node.right, key); } else { // 如果要查找的值等于该节点,说明查找成功,返回改节点 return node; }};function(key, node){
// 同样的,search方法允许在子树中查找值
node = node || root;
return searchNode(key, node);
};
var searchNode = function(key, node){
// 如果node是null,说明树中没有要查找的值,返回false
if (node === null){
return false;
}
if (key < node.key){
// 如果要查找的值小于该节点,继续递归遍历其左侧节点
return searchNode(node.left, key);
} else if (key > node.key){
// 如果要查找的值大于该节点,继续递归遍历其右侧节点
return searchNode(node.right, key);
} else {
// 如果要查找的值等于该节点,说明查找成功,返回改节点
return node;
}
};
this.remove = function(key, node) { // 同样的,允许仅在子树中删除节点 node = node || root; return removeNode(key, node);};var self = this;var removeNode = function(key, node) { // 如果 node 不存在,直接返回 if (node === false) { return null; } // 找到要删除的节点 node = self.search(key, node); // 第一种情况,该节点没有子节点 if (node.left === null && node.right === null) { node = null; return node; } // 第二种情况,该节点只有一个子节点的节点 if (node.left === null) { // 只有右节点 node = node.right; return node; } else if (node.right === null) { // 只有左节点 node = node.left; return node; } // 第三种情况,有有两个子节点的节点 // 将右侧子树中的最小值,替换到要删除的位置 // 找到最小值 var aux = self.min(node.right); // 替换 node.key = aux.key; // 删除最小值 node.right = removeNode(aux.key, node.right); return node;};function(key, node) {
// 同样的,允许仅在子树中删除节点
node = node || root;
return removeNode(key, node);
};
var self = this;
var removeNode = function(key, node) {
// 如果 node 不存在,直接返回
if (node === false) {
return null;
}
// 找到要删除的节点
node = self.search(key, node);
// 第一种情况,该节点没有子节点
if (node.left === null && node.right === null) {
node = null;
return node;
}
// 第二种情况,该节点只有一个子节点的节点
if (node.left === null) {
// 只有右节点
node = node.right;
return node;
} else if (node.right === null) {
// 只有左节点
node = node.left;
return node;
}
// 第三种情况,有有两个子节点的节点
// 将右侧子树中的最小值,替换到要删除的位置
// 找到最小值
var aux = self.min(node.right);
// 替换
node.key = aux.key;
// 删除最小值
node.right = removeNode(aux.key, node.right);
return node;
};
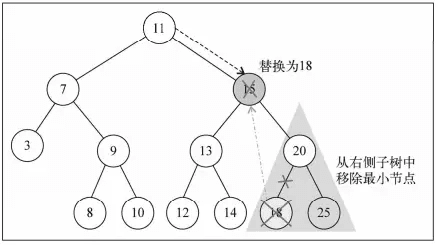
第三种情况的处理过程,如下图所示。当要删除的节点有两个子节点时,为了不破坏树的结构,删除后要替补上来的节点的键值大小必须在已删除节点的左、右子节点的键值之间,且替补上来的节点不应该有子节点,否则会产生一个节点有多个字节点的情况,因此,找右侧子树的最小值替换上来。同理,找左侧子树的最大值替换上来也可以。
this.preOrderTraverse = function(callback){ // 同样的,callback用于对遍历到的节点做操作 preOrderTraverseNode(root, callback);};var preOrderTraverseNode = function (node, callback) { // 遍历到node为null为止 if (node !== null) { callback(node.key); // 先处理当前节点 preOrderTraverseNode(node.left, callback); // 再继续遍历左子节点 preOrderTraverseNode(node.right, callback); // 最后遍历右子节点 }};function(callback){
// 同样的,callback用于对遍历到的节点做操作
preOrderTraverseNode(root, callback);
};
var preOrderTraverseNode = function (node, callback) {
// 遍历到node为null为止
if (node !== null) {
callback(node.key); // 先处理当前节点
preOrderTraverseNode(node.left, callback); // 再继续遍历左子节点
preOrderTraverseNode(node.right, callback); // 最后遍历右子节点
}
};
用先序遍历遍历下图所示的树,并打印节点键值。输出结果:11 7 5 3 6 9 8 10 15 13 12 14 20 18 25。遍历过程如图: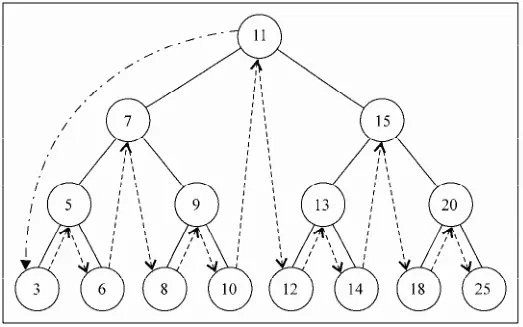
this.inOrderTraverse = function(callback){ // callback用于对遍历到的节点做操作 inOrderTraverseNode(root, callback);};var inOrderTraverseNode = function (node, callback) { // 遍历到node为null为止 if (node !== null) { // 优先遍历左边节点,保证从小到大遍历 inOrderTraverseNode(node.left, callback); // 处理当前的节点 callback(node.key); // 遍历右侧节点 inOrderTraverseNode(node.right, callback); }};function(callback){
// callback用于对遍历到的节点做操作
inOrderTraverseNode(root, callback);
};
var inOrderTraverseNode = function (node, callback) {
// 遍历到node为null为止
if (node !== null) {
// 优先遍历左边节点,保证从小到大遍历
inOrderTraverseNode(node.left, callback);
// 处理当前的节点
callback(node.key);
// 遍历右侧节点
inOrderTraverseNode(node.right, callback);
}
};
对下图的树做中序遍历,并输出各个节点的键值。依次输出:3 5 6 7 8 9 10 11 12 13 14 15 18 20 25。遍历过程如图: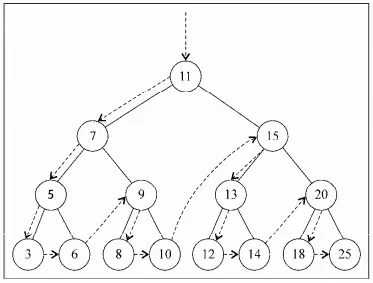
this.postOrderTraverse = function(callback){ postOrderTraverseNode(root, callback);};var postOrderTraverseNode = function (node, callback) { if (node !== null) { postOrderTraverseNode(node.left, callback); //{1} postOrderTraverseNode(node.right, callback); //{2} callback(node.key); //{3} }};function(callback){
postOrderTraverseNode(root, callback);
};
var postOrderTraverseNode = function (node, callback) {
if (node !== null) {
postOrderTraverseNode(node.left, callback); //{1}
postOrderTraverseNode(node.right, callback); //{2}
callback(node.key); //{3}
}
};
可以看到,中序、先序、后序遍历的实现方式几乎一模一样,只是 {1}、{2}、{3} 行代码的执行顺序不同。对下图的树进行后序遍历,并打印键值:3 6 5 8 10 9 7 12 14 13 18 25 20 15 11。遍历过程如图: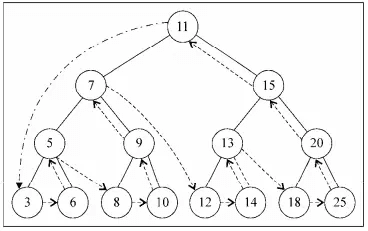
this.print = function() { console.log('root :', root); return root;};function() {
console.log('root :', root);
return root;
};
完整代码请看文件 binary-search-tree.html
测试过程:
// 测试var binarySearchTree = new BinarySearchTree();var arr = [11, 7, 5, 3, 6, 9, 8, 10, 15, 13, 12, 14, 20, 18, 25];for (var i = 0; i < arr.length; i++) { var value = arr[i]; binarySearchTree.insert(value);}console.log('先序遍历:');var arr = [];binarySearchTree.preOrderTraverse(function(value) { // console.log(value); arr.push(value);});console.log('arr :', arr); // [11, 7, 5, 3, 6, 9, 8, 10, 15, 13, 12, 14, 20, 18, 25]var min = binarySearchTree.min();console.log('min:', min); // 3var max = binarySearchTree.max();console.log('max:', max); // 25var search = binarySearchTree.search(10);console.log('search:', search); // 10var remove = binarySearchTree.remove(13);console.log('remove:', remove); // 13console.log('先序遍历:');var arr1 = [];binarySearchTree.preOrderTraverse(function(value) { // console.log(value); arr1.push(value);});console.log('arr1 :', arr1); // [11, 7, 5, 3, 6, 9, 8, 10, 15, 14, 12, 20, 18, 25]console.log('中序遍历:');var arr2 = [];binarySearchTree.inOrderTraverse(function(value) { // console.log(value); arr2.push(value);});console.log('arr2 :', arr2); // [3, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 18, 20, 25]console.log('后序遍历:');var arr3 = [];binarySearchTree.postOrderTraverse(function(value) { // console.log(value); arr3.push(value);});console.log('arr3 :', arr3); // [3, 6, 5, 8, 10, 9, 7, 12, 14, 18, 25, 20, 15, 11]binarySearchTree.print(); // 看控制台
var binarySearchTree = new BinarySearchTree();
var arr = [11, 7, 5, 3, 6, 9, 8, 10, 15, 13, 12, 14, 20, 18, 25];
for (var i = 0; i < arr.length; i++) {
var value = arr[i];
binarySearchTree.insert(value);
}
console.log('先序遍历:');
var arr = [];
binarySearchTree.preOrderTraverse(function(value) {
// console.log(value);
arr.push(value);
});
console.log('arr :', arr); // [11, 7, 5, 3, 6, 9, 8, 10, 15, 13, 12, 14, 20, 18, 25]
var min = binarySearchTree.min();
console.log('min:', min); // 3
var max = binarySearchTree.max();
console.log('max:', max); // 25
var search = binarySearchTree.search(10);
console.log('search:', search); // 10
var remove = binarySearchTree.remove(13);
console.log('remove:', remove); // 13
console.log('先序遍历:');
var arr1 = [];
binarySearchTree.preOrderTraverse(function(value) {
// console.log(value);
arr1.push(value);
});
console.log('arr1 :', arr1); // [11, 7, 5, 3, 6, 9, 8, 10, 15, 14, 12, 20, 18, 25]
console.log('中序遍历:');
var arr2 = [];
binarySearchTree.inOrderTraverse(function(value) {
// console.log(value);
arr2.push(value);
});
console.log('arr2 :', arr2); // [3, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 18, 20, 25]
console.log('后序遍历:');
var arr3 = [];
binarySearchTree.postOrderTraverse(function(value) {
// console.log(value);
arr3.push(value);
});
console.log('arr3 :', arr3); // [3, 6, 5, 8, 10, 9, 7, 12, 14, 18, 25, 20, 15, 11]
binarySearchTree.print(); // 看控制台
结果如下:
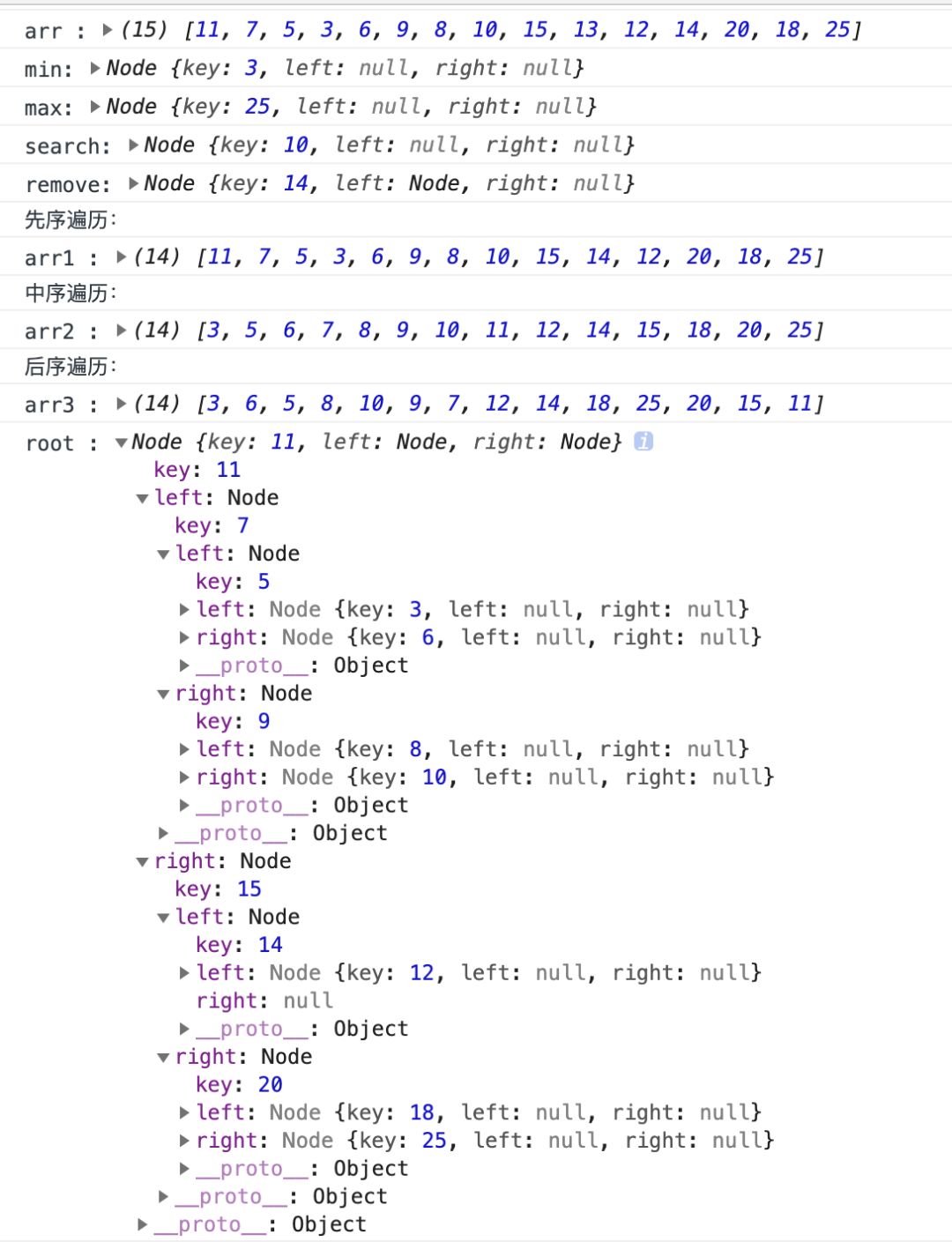
看到这里,你能解答文章的题目 非线性表中的树、堆是干嘛用的 ?其数据结构是怎样的 ?
如果不能,建议再回头仔细看看哦。
3. 文章输出计划
JavaScript 数据结构与算法之美 的系列文章,坚持 3 - 7 天左右更新一篇,暂定计划如下表。
| 标题 | 链接 |
|---|---|
| 时间和空间复杂度 | https://github.com/biaochenxuying/blog/issues/29 |
| 线性表(数组、链表、栈、队列) | https://github.com/biaochenxuying/blog/issues/34 |
| 实现一个前端路由,如何实现浏览器的前进与后退 ? | https://github.com/biaochenxuying/blog/issues/30 |
| 栈内存与堆内存 、浅拷贝与深拷贝 | https://github.com/biaochenxuying/blog/issues/35 |
| 递归 | https://github.com/biaochenxuying/blog/issues/36 |
| 非线性表(树、堆) | https://github.com/biaochenxuying/blog/issues/37 |
| 冒泡排序 | 精彩待续 |
| 插入排序 | 精彩待续 |
| 选择排序 | 精彩待续 |
| 归并排序 | 精彩待续 |
| 快速排序 | 精彩待续 |
| 计数排序 | 精彩待续 |
| 基数排序 | 精彩待续 |
| 桶排序 | 精彩待续 |
| 希尔排序 | 精彩待续 |
| 堆排序 | 精彩待续 |
| 十大经典排序汇总 | 精彩待续 |
如果有错误或者不严谨的地方,请务必给予指正,十分感谢。
4. 最后
上个周六日,不小心看了盗墓笔记电视剧,没忍住,还连看了两部 ??,所以文章更新慢了点。

后面又会恢复 3 - 7 天左右更新一篇,敬请期待。
参考文章:
数据结构与算法之美
学习JavaScript数据结构与算法 — 树
往期精文
1. JavaScript 数据结构与算法之美 - 递归
2. JavaScript 数据结构与算法之美 - 栈内存与堆内存 、浅拷贝与深拷贝
3.JavaScript 数据结构与算法之美 - 线性表 (数组、栈、队列、链表)
4.数据结构与算法之美 - 时间和空间复杂度


喜欢就点个赞吧,听说点在看的都会很有钱。
这篇关于非线性表中的树、堆是干嘛用的 ?其数据结构是怎样的 ?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








