本文主要是介绍必须掌握的八种排序(3-4)--简单选择排序,堆排序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
3、简单选择排序
(1)基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;
然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
(2)理解图
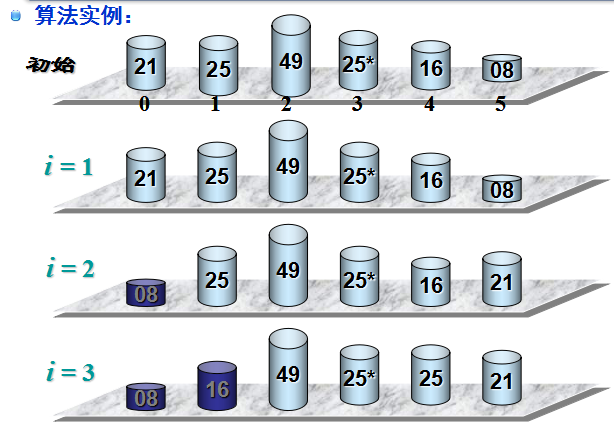
第一次 : 08最小 和21交换位置
第二次: 除第一个位置的08外 16最小 和25交换位置
以此类推
(3)代码实现
public static void selectSort(int[] a) {int position = 0;for (int i = 0; i < a.length; i++) {int j = i + 1;position = i;int temp = a[i];for (; j < a.length; j++) {if (a[j] < temp) {temp = a[j];position = j;}}a[position] = a[i];a[i] = temp;}for (int i = 0; i < a.length; i++)System.out.print(a[i] + "\t");}4、堆排序
(1)基本思想:堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆的定义如下:具有n个元素的序列(h1,h2,…,hn),当且仅当满足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2,…,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最大项(大顶堆)。完全二叉树可以很直观地表示堆的结构。堆顶为根,其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树,调整它们的存储序,使之成为一个堆,这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,二是反复调用渗透函数实现排序的函数。
(2)实例:
初始序列:46,79,56,38,40,84
建堆:
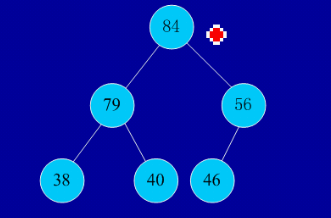
交换,从堆中踢出最大数
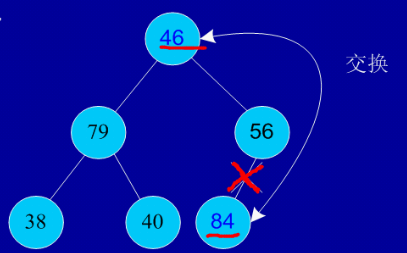
剩余结点再建堆,再交换踢出最大数
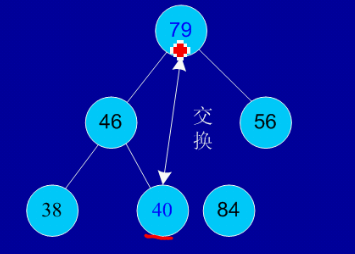
依次类推:最后堆中剩余的最后两个结点交换,踢出一个,排序完成。
(3)代码:
/*** 选择排序之堆排序:* * 1. 基本思想: 堆排序是一树形选择排序,在排序过程中,将R[1..N]看成是一颗完全二叉树的顺序存储结构,* 利用完全二叉树中双亲结点和孩子结点之间的内在关系来选择最小的元素。* * 2. 堆的定义: N个元素的序列K1,K2,K3,...,Kn.称为堆,当且仅当该序列满足特性: Ki≤K2i Ki ≤K2i+1(1≤ I≤[N/2])* 堆实质上是满足如下性质的完全二叉树:树中任一非叶子结点的关键字均大于等于其孩子结点的关键字。例如序列10,15,56,25,30,70就是一个堆,* 它对应的完全二叉树如上图所示。这种堆中根结点(称为堆顶)的关键字最小,我们把它称为小根堆。* 反之,若完全二叉树中任一非叶子结点的关键字均大于等于其孩子的关键字,则称之为大根堆。* * 3.排序过程: 堆排序正是利用小根堆(或大根堆)来选取当前无序区中关键字小(或最大)的记录实现排序的。我们不妨利用大根堆来排序。每一趟排序的基本操作是:* 将当前无序区调整为一个大根堆* ,选取关键字最大的堆顶记录,将它和无序区中的最后一个记录交换。这样,正好和直接选择排序相反,有序区是在原记录区的尾部形成并逐步向前扩大到整个记录区。*/
public class HeapSort {/*** 排序算法的实现,对数组中指定的元素进行排序* * @param array* 待排序的数组* @param c* 比较器*/public void sort(Integer[] arr) {// 创建初始堆initialHeap(arr);/** 对初始堆进行循环,且从最后一个节点开始,直到树只有两个节点止 每轮循环后丢弃最后一个叶子节点,再看作一个新的树*/for (int i = arr.length; i >= 2; i--) {// 根节点与最后一个叶子节点交换位置,即数组中的第一个元素与最后一个元素互换swap(arr, 0, i - 1);// 交换后需要重新调整堆adjustNote(arr, 1, i - 1);}}/*** @param arr* 排序数组* @param c* 比较器*/private void initialHeap(Integer[] arr) {int lastBranchIndex = arr.length / 2;// 最后一个非叶子节点// 对所有的非叶子节点进行循环 ,且从最后一个非叶子节点开始for (int i = lastBranchIndex; i >= 1; i--) {adjustNote(arr, i, arr.length );}}/*** 调整节点顺序,从父、左右子节点三个节点中选择一个最大节点与父节点转换* * @param arr* 待排序数组* @param parentNodeIndex* 要调整的节点,与它的子节点一起进行调整* @param len* 树的节点数* @param c* 比较器*/private void adjustNote(Integer[] arr, int parentNodeIndex, int len) {int maxValueIndex = parentNodeIndex;// 如果有左子树,i * 2为左子树节点索引if (parentNodeIndex * 2 <= len) {// 如果父节点小于左子树时if ((arr[parentNodeIndex - 1].compareTo(arr[parentNodeIndex * 2 - 1])) < 0) {maxValueIndex = parentNodeIndex * 2;// 记录最大索引为左子节点索引}// 只有在有左子树的前提下才可能有右子树,再进一步断判是否有右子树if (parentNodeIndex * 2 + 1 <= len) {// 如果右子树比最大节点更大if ((arr[maxValueIndex - 1].compareTo(arr[(parentNodeIndex * 2 + 1) - 1])) < 0) {maxValueIndex = parentNodeIndex * 2 + 1;// 记录最大索引为右子节点索引}}}// 如果在父节点、左、右子节点三者中,最大节点不是父节点时需要交换,把最大的与父节点交换,创建大顶堆if (maxValueIndex != parentNodeIndex) {swap(arr, parentNodeIndex - 1, maxValueIndex - 1);// 交换后可能需要重建堆,原父节点可能需要继续下沉 因为交换后 maxValueIndex位置的值就不一定是三个节点中最大的了! if (maxValueIndex * 2 <= len) {// 是否有子节点,注,只需判断是否有左子树即可知道adjustNote(arr, maxValueIndex, len);}}}/*** 交换数组中的两个元素的位置* * @param array* 待交换的数组* @param i* 第一个元素* @param j* 第二个元素*/public void swap(Integer[] array, int i, int j) {if (i != j) {// 只有不是同一位置时才需交换Integer tmp = array[i];array[i] = array[j];array[j] = tmp;}}/*** 测试* * @param args*/public static void main(String[] args) {Integer[] a = { 6,9,0,4,5, 9, 1, 4, 2, 6, 3, 8, 0, 7, 0, -7, -1, 34 };HeapSort heapsort = new HeapSort();heapsort.sort(a);for (Integer arrValue : a) {System.out.print(arrValue + " ");}}}
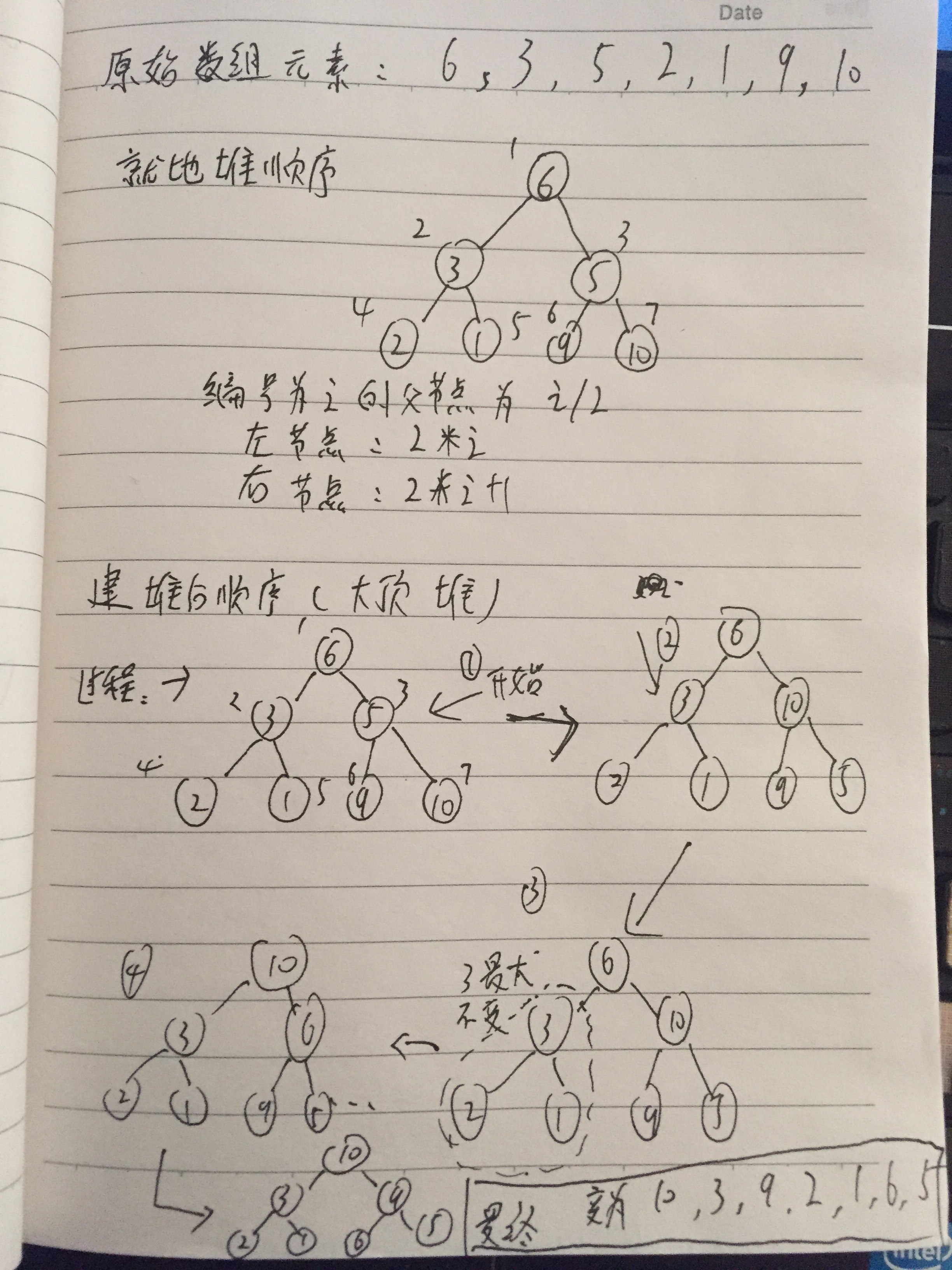
最后 附一张自己的理解图
这篇关于必须掌握的八种排序(3-4)--简单选择排序,堆排序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!