本文主要是介绍【2022 ECCV】《Unstructured Feature Decoupling for Vehicle Re-Identification》,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《Unstructured Feature Decoupling for Vehicle Re-Identification》
文章目录
- 1.Abstract
- 2.Introduction
- 3.Methodology
- 3.1Backbone and Symbol Definition
- 3.2Transformer-based Featuren Decomposing Head
- 3.2.1The Alignment Constraint
- 3.2.2Clustering of Decomposed Features
- 3.2.3Exclusion of Outlier Features
1.Abstract
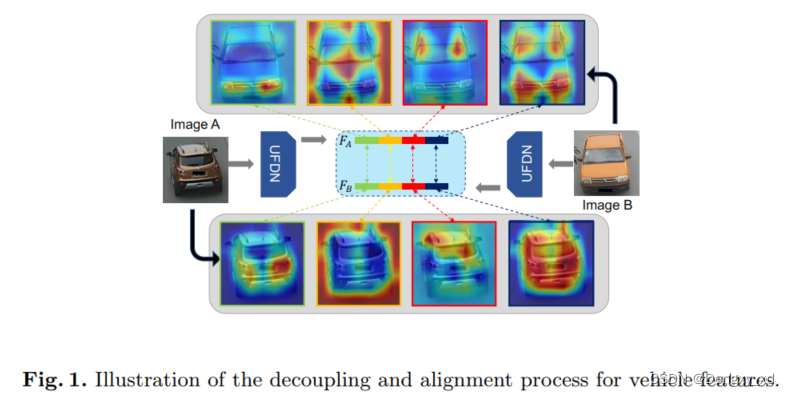
在车辆重识别任务中(Re-Identification,ReID),由于目标姿态和视角等变化导致深度特征无法对齐。以前的方法通过预定义车辆的部件(例如:标志,窗户等)或属性来对齐特征。这些方法由于需要人工手动标注从而计算效率较低。为了在不需要额外标注的情况下对齐深度特征,本文提出了一个非结构特征解耦网络(Unstructured Feature Decoupling Network,UFDN),该网络由一个基于Transformer的特征解耦Head(transformer-based feature decomposing head,TDH)以及一个新的基于聚类解耦约束(cluster-based decoupling constraint,CDC)所组成。 之前的解耦方法所使用的是结构知识,我们目的是获得更多的非结构化特征,其具体多样判别性如图1所示。分解头部的自注意机制有助于模型在全局范围内初步学习判别分解特征。为了进一步学习多样但对齐的解耦特征,我们提出了一个基于聚类的解耦约束,其由一个多样性约束和一个对齐约束所组成。更进一步,我们将对齐约束改进为调整约束来消除异常特征的负面影响,这种异常特征不能在语义上对齐到集群中。广泛的实验表明,所提出的UFDN 在三个流行的Vehicle ReID 基准测试中具有CNN和Transformer主干网,达到了最先进的性能。代码链接: link.
2.Introduction
给定一个查询车辆图像,Vehicle ReID旨在从包含由不相交的摄像机捕获的图像的图库中检索相同车辆的图像。随着深度学习和大规模车辆重识别技术的发展,车辆重识别技术在性能上取得了巨大的提升并广泛运用在智慧城市系统中。然而,处理姿势引起的特征不对齐任具有一定的挑战性。
该文章研究了特征隐式对齐,首先将特征解耦成非结构部件,然后在不使用额外标注的情况下对齐这些特征。然而,主要存在两个挑战:1、如何在不使用额外结构线索的情况下解耦特征?2、如何学习多样但对齐的解耦特征?
本文提出了一个Transformer-based decomposing head(TDH)模块来将车辆特征解耦为非结构部件。TDH通过从通道维度解耦特征图,其保持了每个解耦特征的全局接受域。我们将每个解耦特征图组输入到一个改进的transformer block中,然后子注意力机制能够自动在全局角度编码具有判别性特征。因为特征图不能简单地划分为固定的条纹或网格,解耦特征在没有额外线索的情况下能够隐式学习判别性语义信息。
除了隐式解耦模块,我们提出了一个新的基于聚类的解耦约束(CDC),以无标注的形式提高分解特征的多样性和一致性。CDC的目的是将分类的特征聚类成组,其中包括:
- 多样性约束:分解特征应当是相互正交的,这样就促使它们关注不同的区域。
- 对齐约束:分解的特征应当靠近相关的聚类中心,以便彼此对齐。
然而,一些异常特征在语义中并不能对齐聚类中心,会导致无用甚至降低准确率。为了解决这一问题,本文通过过滤异常特征来减轻它们所带来的负面影响并将最后的输出定义为解耦特征。文章所提出的UFDN旨在保证一维特征的多样性。
于此同时,我们从不同的角度对样本进行可视化,如图1 所示。并发现相应的解耦特征倾向于关注相似的显著区域(例如,第一部分的灯光信息以及和第二部分的前端信息等)。本文方法所提出的方法称为非结构化特征解耦网络(UFDN),并在具有两个不同主干(ResNet和swing -transformer)的三个流行基准上进行实验,以评估UFDN的有效性。
本文的主要贡献如下:
- 本文提出UFDN模型其目的通过在无人为标注的情况下将特征解耦为非结构,多样以及对齐部件以减轻车辆重识别任务中深度特征不齐现象。
- 基于transofrmer的非结构化特征分解头可以在全局范围内从通道维度将特征分解成若干组,比局部指定的方法具有更强的鲁棒性。
- 我们提出了基于聚类的解耦约束来保证解耦特征在没有人为标注的情况下能够保证多样以及对齐,此外减轻外部异常值的影响。
- 在没有人为标注的情况下,本文所提出的UFDN在三个benchmark上均优于其他方法。
3.Methodology
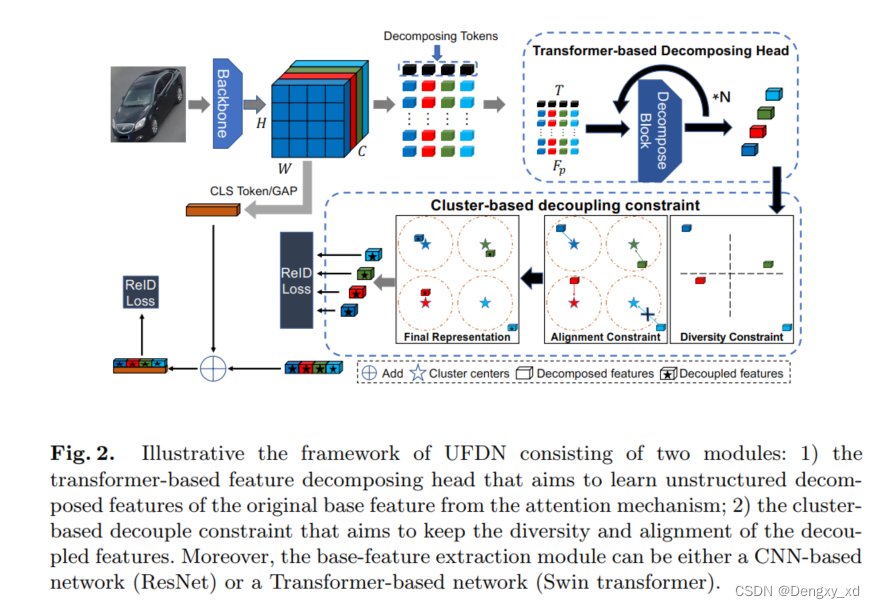
图2为UFDN的示意图,其主要由基于transformer的特征解耦头和基于聚类的解耦约束所组成。
3.1Backbone and Symbol Definition
给定一个输入图像 X X X,主干输出一个特征图,将该特征图重新调整为一个基础特征 F b a s e ∈ R n × c F_{base} \in \mathcal{R}^{n \times c} Fbase∈Rn×c,这里 n = H × W n=H \times W n=H×W和 c c c分别表示空间维度和通道维度。然后,本文按照通道维度将 F b a s e F_{base} Fbase分解成 k k k个组则获得一个特征集合 F p ∈ R k × n × m F_{p} \in \mathcal{R}^{k \times n \times m} Fp∈Rk×n×m,这里 c = k × m c = k \times m c=k×m。这里的主干网络可以是基于CNN的也可以是基于Transformer的。
3.2Transformer-based Featuren Decomposing Head
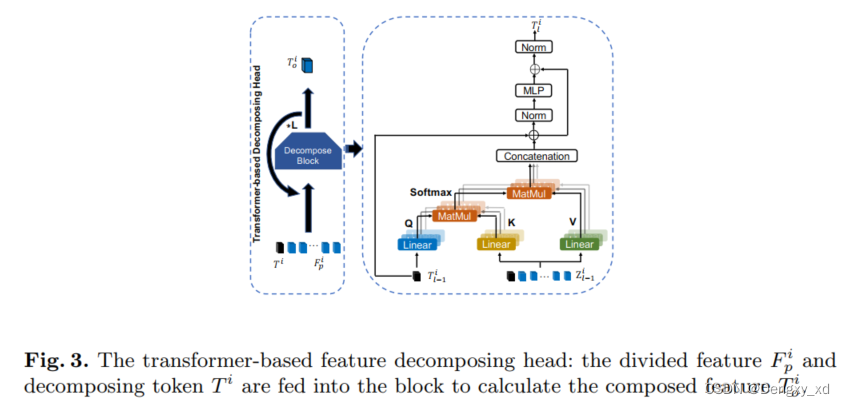
基于Transformer的特征解耦头(TDH)编码了每个解耦特征的非结构信息 F p ∗ i ∈ R n × m F_{p}*{i} \in \mathcal{R}^{n \times m} Fp∗i∈Rn×m, i = 1 , 2 , 3 , . . . , k i=1,2,3,...,k i=1,2,3,...,k。如图2所示, k k k个分解令牌 T i ∈ R m T^{i} \in \mathcal{R}^{m} Ti∈Rm分别预挂载在相关通道特征上 F p i ∈ R n × m F_{p}^{i} \in \mathcal{R}^{n \times m} Fpi∈Rn×m。输入序列 z 0 i = [ T i , F p i ] z_{0}^{i}=[T^{i},F_{p}^{i}] z0i=[Ti,Fpi]被输入到基于transformer特征解耦头中。
如图三所示,TDH共包含了L个transformer blocks,每个block包含一个多头解耦注意力模块以及一个MLP模块。由于 F p i F_{p}^{i} Fpi是深层特征其很好地编码了判别性信息,我们依照[1]设计只更新解耦令牌 T i T^{i} Ti来重新聚合 F p i F_{p}^{i} Fpi。 F p i F_{p}^{i} Fpi在训练过程中被冻结以减少计算消耗。给定义一个输入序列 z 0 i = [ T i , F p i ] z_{0}^{i}=[T^{i},F_{p}^{i}] z0i=[Ti,Fpi],本文将TDH当中第 l − 1 l-1 l−1个输出解耦令牌记作 T l − 1 i T_{l-1}^{i} Tl−1i并且输入第 l l l个block的输入序列记作 z l − 1 i = [ T l − 1 i , F p i ] z_{l-1}^{i}=[T_{l-1}^{i},F_{p}^{i}] zl−1i=[Tl−1i,Fpi]。然后,将第 l l l个输入序列 z l − 1 i z_{l-1}^{i} zl−1i输入TDH第 l l l个block的DA模块,其可以被写作:
Q = W q T l − 1 i Q=W_{q}T_{l-1}^{i} Q=WqTl−1i, K = W k z l − 1 i K=W_{k}z_{l-1}^{i} K=Wkzl−1i, V = W v z l − 1 i V=W_{v}z_{l-1}^{i} V=Wvzl−1i,
A = S o f t m a x ( Q K T ) A=Softmax(QK^{T}) A=Softmax(QKT), h l i = A ⋅ V + T l − 1 i h_{l}^{i}=A \cdot V+T_{l-1}^{i} hli=A⋅V+Tl−1i,
这里 W q , W k , W v ∈ R m × m W_q,W_k,W_v \in \mathcal{R}^{m \times m} Wq,Wk,Wv∈Rm×m是投影矩阵。从多头解耦注意力模块中得到隐变量 h l i h_{l}^{i} hli,并将其输入到MLP模块中,
T l i = L N ( M L P ( L N ( h l i ) ) + h l i ) T_{l}^{i}=LN(MLP(LN(h_{l}^{i}))+h_{l}^{i}) Tli=LN(MLP(LN(hli))+hli),
这里MLP和LN分别表示MLP模型以及归一化层。然后,将解耦令牌 T l i T_{l}^{i} Tli与 F p i F_{p}^{i} Fpi连接起来作为输入序列 z l + 1 i z_{l+1}^{i} zl+1i输入到下一个block。
令TDH最后一个block输出的为解耦令牌 T o i = T L i T_{o}^{i}=T_{L}^{i} Toi=TLi,并且相关的全局特征作为解耦特征 F i ∈ R m F^{i} \in \mathcal{R}^{m} Fi∈Rm:
F i = T o i + G A P ( F p i ) F^{i}=T_{o}^{i}+GAP(F_{p}^{i}) Fi=Toi+GAP(Fpi)
这里GAP表示全局平均池化。最后, k k k个解耦特征 [ F 1 , F 2 , . . . , F k ] [F^{1},F^{2},...,F^{k}] [F1,F2,...,Fk]被连接起来为最终的ReID特征 F ∈ R c F \in \mathcal{R}^{c} F∈Rc.本文对每个分解的特征执行ReID损失,ReID特征如下:
L T H D = L R e I D ( F ) + ∑ i = 1 k L R e I D ( F i ) L_{THD}=L_{ReID}(F)+\sum_{i=1}^{k}L_{ReID}(F^{i}) LTHD=LReID(F)+∑i=1kLReID(Fi),
L R e I D = L c e + L t r i L_{ReID}=L_{ce}+L_{tri} LReID=Lce+Ltri,
这里 L c e L_{ce} Lce表示交叉熵损失, L t r i L_{tri} Ltri表示三元组损失。
##The Cluster-based Decoupling Constraint
除了隐式特征解耦模块,一个基于聚类解耦约束(CDC)被提出来获得解耦特征,要求分解后的特征具有多样性以及对齐性,如图2所示。首先,我们使用一个多样性约束来强制解耦特征的多样性。然后,来对齐不同图像的解耦特征,我们提出了一个对齐约束其聚类了组内的相关解耦特征,并消除了异常特征值的负面影响。
###The Diversity Constraint
给定一个输入图像 X X X,我们得到 k k k个解耦特征 F = [ F 1 , F 2 , . . . , F k ] F=[F^{1},F^{2},...,F^{k}] F=[F1,F2,...,Fk]并希望它们每一个应当具有不同的感兴趣的语义区域。提高解耦特征的多样性能够钱模型去挖掘更多突出以及判别性的信息并加速车辆特征解耦过程。将这个需求抽象为数学描述,我们约束这些特征彼此之间是正交的。多样性约束限制特征 F F F的Gram矩阵在Frobenius范数下趋近于单位阵。
L d i v = ∣ ∣ F F T − I ∣ ∣ F L_{div}=\lvert\lvert FF^{T}-I\rvert\rvert_{F} Ldiv=∣∣FFT−I∣∣F
Gram矩阵式两两向量的内积组成的,所以Gram矩阵可以反应出该组向量中各个向量之间的某种关系
3.2.1The Alignment Constraint
多样性约束只是关注同一张图像当中的特征关系,忽略了不同图像之间的关系。因此本文提出一个对齐约束其以相同的顺序排列不同图像的解耦特征。例如:给定两张图像 X 1 X_1 X1和 X 2 X_2 X2,得到对应的解耦特征 F 1 = [ F 1 1 , F 1 2 , . . . , F 1 k ] F_1=[F_{1}^{1},F_{1}^{2},...,F_{1}^{k}] F1=[F11,F12,...,F1k]和 F 2 = [ F 2 1 , F 2 2 , . . . , F 2 k ] F_2=[F_{2}^{1},F_{2}^{2},...,F_{2}^{k}] F2=[F21,F22,...,F2k],并且为每个组的解耦特征建立一个聚类中心,并要求解耦特征应当接近相关的聚类中心以便彼此分离。
3.2.2Clustering of Decomposed Features
给定 M M M个样本,将其分解为 K K K个分解特征并为每一组解耦特征 [ F 1 i , F 2 i , . . . , F M i ] , i ∈ [ 1 , k ] [F_{1}^{i},F_{2}^{i},...,F_{M}^{i}], i \in [1,k] [F1i,F2i,...,FMi],i∈[1,k]建立一个聚类中心 C i C^{i} Ci。
C i = 1 M ∑ j = 1 M F j i C^{i}=\frac{1}{M} \sum_{j=1}^{M}F_{j}^{i} Ci=M1∑j=1MFji,
这里 F j i F_{j}^{i} Fji是样本 X j X_{j} Xj的第 i i i个解耦特征。在训练前期,解耦特征会经历较大的波动,这是因为来自损失反向传播导致网络有较大的调整,这将导致聚类中心收敛过程不稳定,为了聚类中心平滑收敛,采用动量策略来更新类簇中心。
C t i = α C t − 1 i + ( 1 − α ) 1 M ∑ j = 1 M F j i C_{t}^{i}=\alpha C_{t-1}^{i}+(1 - \alpha)\frac{1}{M} \sum_{j=1}^{M}F_{j}^{i} Cti=αCt−1i+(1−α)M1∑j=1MFji,
这里 α \alpha α是控制聚类中心更新速度的权重, t t t表示训练过程的不同时期。我们将聚类中心 C i C^{i} Ci视为标准特征中心,因为其已经遍历了当前epoch当中所有的样本,学习到了更通用以及全面的特征表示。
在为每组特征构建聚类中心后,我们约束正例( F j i 和其对应的类中心 C i F_{j}^{i}和其对应的类中心C^i Fji和其对应的类中心Ci)对之间的距离应当小于负例对(其它类中心)之间的距离。
K a l i g n = [ d ( F j i , C i ) − m i n ( d ( F j i , C q ∈ [ 1 , k ] , q ≠ i ) ) + θ ) ] + K_{align}=[d(F_{j}^{i},C^{i})-min(d(F_{j}^{i},C^{q\in[1,k],q\neq i}))+ \theta )]^{+} Kalign=[d(Fji,Ci)−min(d(Fji,Cq∈[1,k],q=i))+θ)]+
这里 d ( a , b ) d(a,b) d(a,b)度量了 a a a和 b b b之间的距离, [ ⋅ ] + = m a x ( ⋅ , 0 ) [\cdot]^{+}=max(\cdot,0) [⋅]+=max(⋅,0), θ \theta θ是控制正例对与负例对之间的距离阈值。在用多样性约束和对齐约束约束分解特征后,我们将其称为解耦特征。
3.2.3Exclusion of Outlier Features
一些解耦特征可能缺少聚类中心的语义信息,由于不同视角或姿态,我们称为离群特征。离群特征在语义上并不能对齐到聚类中心,例如:当图像是从后面拍摄的,前窗的信息则是丢失的,这将导致性能降低。因此,有必要通过排除异常特征相应的对准损失反向传播来消除异常特征所带来的负面影响。
首先,我们计算每个中心 C i C^{i} Ci的平均距离 D i D_{i} Di:
D i = 1 M ∑ j = 1 M d ( F j i , C i ) D_{i}=\frac{1}{M}\sum_{j=1}^{M}d(F_{j}^{i},C^{i}) Di=M1∑j=1Md(Fji,Ci).
然后如果 F j i F_{j}^{i} Fji到其对应的聚类中心的距离大于平均距离 D i D_i Di,我们则剔除该损失。
L m o d = L a l i g n , i f d ( F j i , C i ) < D i L_{mod}=L_{align}, if d(F_{j}^{i},C^{i}) < D_{i} Lmod=Lalign,ifd(Fji,Ci)<Di
L m o d = 0 , i f d ( F j i , C i ) ≥ D i L_{mod}=0, if d(F_{j}^{i},C^{i}) \geq D_{i} Lmod=0,ifd(Fji,Ci)≥Di
基于聚类的解耦约束计算为:
L C D C = 1 M ∑ j = 1 M [ L d i v ( F j ) + ∑ i = 1 k L m o d ( F j i , C i , D i ) ] L_{CDC}=\frac{1}{M} \sum_{j=1}^{M}[L_{div}(F_{j}) + \sum_{i=1}^{k}L_{mod}(F_{j}^{i},C^{i},D_{i})] LCDC=M1∑j=1M[Ldiv(Fj)+∑i=1kLmod(Fji,Ci,Di)]
最终,UFDN的损失是 L = L T H D + L C D C L = L_{THD}+L_{CDC} L=LTHD+LCDC
这篇关于【2022 ECCV】《Unstructured Feature Decoupling for Vehicle Re-Identification》的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








