算法打卡day15|二叉树篇04|110.平衡二叉树、257. 二叉树的所有路径、404.左叶子之和

本文主要是介绍算法打卡day15|二叉树篇04|110.平衡二叉树、257. 二叉树的所有路径、404.左叶子之和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

算法题

Leetcode 110.平衡二叉树

题目链接:110.平衡二叉树

大佬视频讲解：平衡二叉树视频讲解

个人思路

可以用递归法，计算左右子树的高度差，当超过1时就不为平衡二叉树了；

解法

回顾一下二叉树节点的深度与高度；

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

在leetcode中深度从1开始的，有些地方从0开始；

递归法

类似于二叉树的后序遍历，即对于当前遍历到的节点：先递归地判断其左右子树是否平
衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度(高度一定
是非负整数)，否则返回 -1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。

如果是用前序遍历，则对于同一个节点，函数 getHeight 会被重复调用，导致时间复杂
度较高。如果使用后序遍历的做法，则对于每个节点，函数 height 只会被调用一次。

也可以这样记忆，当树节点高度与深度不同时，求深度可以从上到下去查所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

class Solution {public boolean isBalanced(TreeNode root) {//1.确定递归函数参数以及返回值return getHeight(root) != -1;//判断是否为平衡二叉树}private int getHeight(TreeNode root) {if (root == null) {//根；前序遍历，先遍历根；return 0;}//3.确定单层递归逻辑int leftHeight = getHeight(root.left);//左if (leftHeight == -1) {return -1;}int rightHeight = getHeight(root.right);//右if (rightHeight == -1) {return -1;}// 左右子树高度差大于1，return -1表示已经不是平衡树了if (Math.abs(leftHeight - rightHeight) > 1) {//2.确定递归终止条件return -1;}return Math.max(leftHeight, rightHeight) + 1;}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（使用二叉树）

迭代法

用栈来模拟后序遍历，遍历每一个节点的时候，再去判断左右孩子的高度是否符合，其中利用TreeNode.val来保存当前结点的高度，这样就不会有重复遍历；

class Solution {public boolean isBalanced(TreeNode root) {if (root == null) {return true;}Stack<TreeNode> stack = new Stack<>();TreeNode pre = null;while (root != null || !stack.isEmpty()) {while (root != null) {stack.push(root);root = root.left;}TreeNode inNode = stack.peek();// 右结点为null或已经遍历过if (inNode.right == null || inNode.right == pre) {// 输出if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {return false;}stack.pop();pre = inNode;root = null;// 当前结点下，没有要遍历的结点了} else {root = inNode.right;// 右结点还没遍历，遍历右结点}}return true;}// 求结点的高度public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = root.left != null ? root.left.val : 0;int rightHeight = root.right != null ? root.right.val : 0;int height = Math.max(leftHeight, rightHeight) + 1;root.val = height;// 用TreeNode.val来保存当前结点的高度return height;}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);(一个栈的空间，最差情况下与树的空间一样，那就是n）

Leetcode 257. 二叉树的所有路径

题目链接:257. 二叉树的所有路径

大佬视频讲解:二叉树的所有路径视频讲解

个人思路

就知道好像是用回溯，但不记得怎么实现了

解法

递归法

要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径，因为要返回根到叶子结点的路径，所以肯定是需要回溯的，递归和回溯就是一家的；

因为是要记录到叶子节点的路径，所以左右孩子为空则为终止条件，到遍历到叶子节点，则将结果打印放入数组，然后回溯继续递归；

在写代码时，要记住回溯和递归是一一对应的，有一个递归，就要有一个回溯；

class Solution {public List<String> binaryTreePaths(TreeNode root) {//1.确定递归函数参数以及返回值List<String> res = new ArrayList<>();// 存最终的结果if (root == null) {return res;}List<Integer> paths = new ArrayList<>();// 作为结果中的路径traversal(root, paths, res);return res;}private void traversal(TreeNode root, List<Integer> paths, List<String> res) {paths.add(root.val);// 前序遍历，中// 遇到叶子结点if (root.left == null && root.right == null) {//2.确定递归终止条件// 输出StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串for (int i = 0; i < paths.size() - 1; i++) {sb.append(paths.get(i)).append("->");}sb.append(paths.get(paths.size() - 1));// 记录最后一个节点res.add(sb.toString());// 收集一个路径return;}//3.确定单层递归逻辑// 递归和回溯是同时进行，所以要放在同一个花括号里if (root.left != null) { // 左traversal(root.left, paths, res);//有一个递归，就要有一个回溯paths.remove(paths.size() - 1);// 回溯}if (root.right != null) { // 右traversal(root.right, paths, res);//有一个递归，就要有一个回溯paths.remove(paths.size() - 1);// 回溯}}
}

时间复杂度:O(n^2)；（每遍历一条路径都要拷贝数据，高度乘节点，所以是n*n）

空间复杂度:O(n^2);（递归遍历暂存字符与结果，都需要空间）

迭代法

使用前序遍历的迭代方式来模拟遍历路径的过程


class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> result = new ArrayList<>();if (root == null)return result;Stack<Object> stack = new Stack<>();// 节点和路径同时入栈stack.push(root);stack.push(root.val + "");while (!stack.isEmpty()) {// 节点和路径同时出栈String path = (String) stack.pop();TreeNode node = (TreeNode) stack.pop();// 若找到叶子节点if (node.left == null && node.right == null) {result.add(path);}//右子节点不为空if (node.right != null) {stack.push(node.right);stack.push(path + "->" + node.right.val);}//左子节点不为空if (node.left != null) {stack.push(node.left);stack.push(path + "->" + node.left.val);}}return result;}
}

时间复杂度:O(n^2)；（每遍历一条路径都要拷贝数据）

空间复杂度:O(n);（使用两个栈，一个存数据，一个遍历）

Leetcode 404.左叶子之和

题目链接:404.左叶子之和

大佬视频讲解:左叶子之和视频讲解

个人思路

可以用层序遍历，遍历到最后一层时，将左叶子筛选出来，结果值累加；

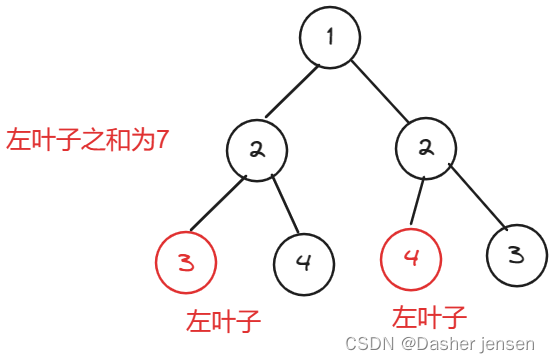
解法

递归法

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

递归三部曲

1.确定递归函数的参数和返回值

判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int

2.确定终止条件

如果遍历到空节点，那么左叶子值一定是0

注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0：

3.确定单层递归的逻辑

当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和右子树左叶子之和，相加便是整个树的左叶子之和。

class Solution {public int sumOfLeftLeaves(TreeNode root) {if (root == null) return 0;int leftValue = sumOfLeftLeaves(root.left);    // 左int rightValue = sumOfLeftLeaves(root.right);  // 右int midValue = 0;//判断是否为左叶子节点if (root.left != null && root.left.left == null && root.left.right == null) { midValue = root.left.val;}int sum = midValue + leftValue + rightValue;  // 中return sum;}
}

时间复杂度:O(n)；（遍历二叉树）

空间复杂度:O(n);（递归栈）

迭代法

层序遍历迭代法，采用前序遍历，在模板代码的基础上判断当前节点的子节点是否左叶子，并累加值；

class Solution {public int sumOfLeftLeaves(TreeNode root) {int sum = 0;//左叶子节点和if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();while (size -- > 0) {TreeNode node = queue.poll();//判断是否为左叶子节点if (node.left != null) { // 左节点不为空queue.offer(node.left);if (node.left.left == null && node.left.right == null){ // 左叶子节点sum += node.left.val;}}if (node.right != null) queue.offer(node.right);}}return sum;}
}