本文主要是介绍算法刷题day29:区间合并,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 引言
- 概念
- 一、挤牛奶
- 二、区间合并
- 三、校门外的树
- 四、管道
引言
区间合并这种题,是比较小的题,一般是不会直接出成一道题来考你的,一般思路都是给一道题,里面包含了各种的点,每一个点都需要一个想区间合并这样的知识点来破解,所以会是很重要的,并且要能抽象出各种模型的能力也是非常重要的,加油!
概念
区间合并:其实就是个模板,可以参考我之前写过的博客 区间合并
一、挤牛奶
标签:区间合并
思路:就是按区间合并的模板,当前遍历的区间已经不能合并了,那么就可以计算出上一个区间的长度了,也可以求出来中间空出了多长的区间,统计一下各自的最大值即可。最后一个区间不论是什么情况,它的长度都不会被算进来,所以需要最后单独比较一下最后一个区间的长度。
题目描述:
每天早上 5 点,三名农夫去牛场给奶牛们挤奶。现在从 5 点开始按秒计时,第一名农夫在第 300 秒开始给牛挤奶,并在第 1000 秒停止挤奶。第二名农夫在第 700 秒开始给牛挤奶,并在第 1200 秒停止挤奶。第三名农夫在第 1500 秒开始给牛挤奶,并在第 2100 秒停止挤奶。从开始挤奶到挤奶完全结束,这一期间,至少存在一名农夫正在挤奶的连续时间段的长度最长为 900 秒(第 300 秒至第 1200 秒),完全没有任何农夫在挤奶的连续时间段的长度最长为 300 秒(第 1200 秒至第 1500 秒)。现在给你 N 名农夫挤 N 头奶牛的工作时间表,请你求出:至少存在一名农夫正在挤奶的连续时间段的最长长度。
没有任何农夫在挤奶的连续时间段的最长长度。
注意:本题中给出的所有时间均为时刻(时间点),因此在本题中挤奶区间 [100,200] 和 [201,300] 中间会有长度为 1 秒的间歇时间。输入格式
第一行包含整数 N,表示农夫数量。接下来 N 行,每行包含两个非负整数 l,r,表示农夫挤奶的开始时刻和结束时刻。输出格式
共一行,包含两个整数,分别表示最长连续挤奶时间以及最长连续无人挤奶时间。数据范围
1≤N≤5000,0≤l≤r≤106
输入样例:
3
300 1000
700 1200
1500 2100
输出样例:
900 300
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 5010;int n;
PII segs[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 0; i < n; ++i) cin >> segs[i].x >> segs[i].y;sort(segs, segs+n);int res1 = 0, res2 = 0;int l = segs[0].x, r = segs[0].y;for(int i = 1; i < n; ++i){if(segs[i].x > r){res1 = max(res1, r - l);res2 = max(res2, segs[i].x - r);l = segs[i].x, r = segs[i].y;}else{r = max(r, segs[i].y);}}res1 = max(res1, r - l);cout << res1 << " " << res2 << endl;return 0;
}
二、区间合并
标签:区间合并、模板题
思路:模板题没什么说的。
题目描述:
给定 n 个区间 [li,ri],要求合并所有有交集的区间。注意如果在端点处相交,也算有交集。输出合并完成后的区间个数。例如:[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。输入格式
第一行包含整数 n。接下来 n 行,每行包含两个整数 l 和 r。输出格式
共一行,包含一个整数,表示合并区间完成后的区间个数。数据范围
1≤n≤100000,−109≤li≤ri≤109
输入样例:
5
1 2
2 4
5 6
7 8
7 9
输出样例:
3
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10;int n;
PII segs[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 0; i < n; ++i) cin >> segs[i].x >> segs[i].y;sort(segs, segs+n);int res = 0;int l = -2e9, r = -2e9;for(int i = 0; i < n; ++i){if(segs[i].x > r){res++;l = segs[i].x, r = segs[i].y;}else{r = max(r, segs[i].y);}}cout << res << endl;return 0;
}
三、校门外的树
标签:区间合并、差分
思路1:看到在一个区域内操作,并且结果看的是有没有操作过,我就知道可以用差分了。差分就是使用 O ( 1 ) O(1) O(1) 的时间复杂度在 [ l , r ] [l,r] [l,r] 的范围内加上一个数,值得注意的是,区间是从 [0,n] 的,差分的下标需要从 1 1 1 开始,所以我们只要把所有的位置向后偏移一位即可,剩下的就是常规操作了,最后看从 [ 1 , n + 1 ] [1,n+1] [1,n+1] 中有几个没有被操作过,累加即可。差分可以看我以前的博客 前缀和与差分
思路2:这道题跟挤牛奶那道题很像,只不过挤牛奶那道题给出的数据左边界已经给了,而这道题给出的数据有可能还不挨左边界,并且该题的合并的条件不同,条件是树,只要树移了就算连着,比如 [ 1 , 2 ] , [ 3 , 4 ] [1,2],[3,4] [1,2],[3,4] 能合并成 [ 1 , 4 ] [1,4] [1,4] ,所以条件得改一下,并且初始的 l , r l,r l,r 也要好好考虑一下初始值,使得不用特判。详情见代码。
题目描述:
某校大门外长度为 L 的马路上有一排树,每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴,马路的一端在数轴 0 的位置,另一端在 L 的位置;数轴上的每个整数点,即 0,1,2,……,L,都种有一棵树。由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。输入格式
输入文件的第一行有两个整数 L 和 M,L 代表马路的长度,M 代表区域的数目,L 和 M 之间用一个空格隔开。接下来的 M 行每行包含两个不同的整数,用一个空格隔开,表示一个区域的起始点和终止点的坐标。输出格式
输出文件包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。数据范围
1≤L≤10000,1≤M≤100
输入样例:
500 3
150 300
100 200
470 471
输出样例:
298
示例代码1: 差分
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 10010;int n, m;
int b[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;while(m--){int l, r;cin >> l >> r;l++, r++;b[l]++, b[r+1]--;}for(int i = 1; i <= n + 1; ++i){b[i] += b[i-1]; }int res = 0;for(int i = 1; i <= n + 1; ++i){if(!b[i]) res++; }cout << res << endl;return 0;
}
示例代码2: 区间合并
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 110;int n, m;
PII segs[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 0; i < m; ++i) cin >> segs[i].x >> segs[i].y;sort(segs, segs+m);int res = 0;int l = -1, r = -1;for(int i = 0; i < m; ++i){if(segs[i].x > r + 1){res += segs[i].x - r - 1;l = segs[i].x, r = segs[i].y;}else{r = max(r, segs[i].y);}}res += n - r;cout << res << endl;return 0;
}
四、管道
标签:二分、区间合并
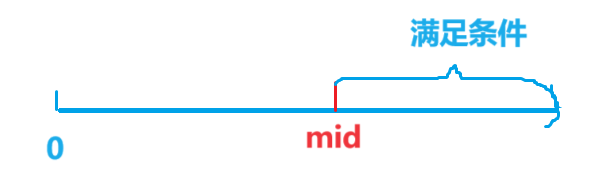
思路:一般求最值都是可以用二分出来的,假如最短时间为 m i d mid mid ,那么大于等于 m i d mid mid 的都是满足条件的,而小于 m i d mid mid 的都是不满足条件的,也就是该题具有二段性,性质如下图所示。所以我们可以用二分来枚举找到边界。对于 c h e c k check check 函数,可以将在 m i d mid mid 时间当前阀门流过的水的范围看作一个区间,如果所有的区间合并为整个管道,那么就满足。值得注意的是,这道题也是不需要边界挨着,只要是区间相邻就可以合并(由题意可知)。
题目描述:
有一根长度为 len 的横向的管道,该管道按照单位长度分为 len 段,每一段的中央有一个可开关的阀门和一个检测水流的传感器。一开始管道是空的,位于 Li 的阀门会在 Si 时刻打开,并不断让水流入管道。对于位于 Li 的阀门,它流入的水在 Ti(Ti≥Si)时刻会使得从第 Li−(Ti−Si) 段到第 Li+(Ti−Si) 段的传感器检测到水流。求管道中每一段中间的传感器都检测到有水流的最早时间。输入格式
输入的第一行包含两个整数 n,len,用一个空格分隔,分别表示会打开的阀门数和管道长度。接下来 n 行每行包含两个整数 Li,Si,用一个空格分隔,表示位于第 Li 段管道中央的阀门会在 Si 时刻打开。输出格式
输出一行包含一个整数表示答案。数据范围
对于 30% 的评测用例,n≤200,Si,len≤3000;
对于 70% 的评测用例,n≤5000,Si,len≤105;
对于所有评测用例,1≤n≤105,1≤Si,len≤109,1≤Li≤len,Li−1<Li。输入样例:
3 10
1 1
6 5
10 2
输出样例:
5
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10;int n, m;
int L[N], S[N];
PII segs[N];bool check(int mid)
{int cnt = 0;for(int i = 0; i < n; ++i){if(mid >= S[i]){int t = mid - S[i];int l = max(1, L[i] - t), r = min((LL)m, (LL)L[i] + t);segs[cnt++] = {l,r};}}sort(segs, segs+cnt);int l = -2e9, r = -2e9;for(int i = 0; i < cnt; ++i){if(segs[i].x > r + 1) {l = segs[i].x, r = segs[i].y;}else{r = max(r, segs[i].y);}}return l == 1 && r == m;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 0; i < n; ++i) cin >> L[i] >> S[i];int l = 1, r = 2e9;while(l < r){int mid = (LL)l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << r << endl;return 0;
}
这篇关于算法刷题day29:区间合并的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







